Zero-dimensional space
Encyclopedia
In mathematics
, a zero-dimensional topological space is a topological space
that has dimension zero with respect to one of several inequivalent notions of assigning a dimension
to a given topological space. Specifically:
The two notions above agree for separable, metrisable spaces.
is necessarily totally disconnected, but the converse fails.
However a locally compact Hausdorff space is zero-dimensional if and only if it is totally disconnected. (See for the non-trivial direction.)
Zero-dimensional Polish space
s are a particularly convenient setting for descriptive set theory
. Examples of such spaces include the Cantor space
and Baire space
.
Hausdorff zero-dimensional spaces are precisely the subspaces
of topological powers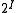
where 2={0,1} is given the discrete topology. Such a space is sometimes called a Cantor cube. If 
is countably infinite
,
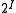is the Cantor space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a zero-dimensional topological space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that has dimension zero with respect to one of several inequivalent notions of assigning a dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
to a given topological space. Specifically:
- A topological space is zero-dimensional with respect to the Lebesgue covering dimensionLebesgue covering dimensionLebesgue covering dimension or topological dimension is one of several inequivalent notions of assigning a topological invariant dimension to a given topological space.-Definition:...
if every open cover of the space has a refinement which is a coverCover (topology)In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of the space by open sets such that any point in the space is contained in exactly one open set of this refinement. - A topological space is zero-dimensional with respect to the small inductive dimension if it has a baseBase (topology)In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
consisting of clopen setClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
s.
The two notions above agree for separable, metrisable spaces.
Properties of spaces with covering dimension zero
A zero-dimensional Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is necessarily totally disconnected, but the converse fails.
However a locally compact Hausdorff space is zero-dimensional if and only if it is totally disconnected. (See for the non-trivial direction.)
Zero-dimensional Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
s are a particularly convenient setting for descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
. Examples of such spaces include the Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
and Baire space
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
.
Hausdorff zero-dimensional spaces are precisely the subspaces
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
of topological powers
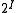where 2={0,1} is given the discrete topology. Such a space is sometimes called a Cantor cube. If is countably infiniteCountable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
,
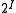is the Cantor space.