Parallelization (mathematics)
Encyclopedia
In mathematics
, a parallelization of a manifold
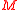of dimension n is a set of n global linearly independent vector field
s.
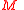of dimension n, a parallelization of 
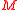is a set 
of n vector fields defined on all of 
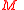such that for every 
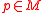the set 
is a basis of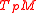 
, where 
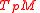denotes the fiber over 
of the tangent vector bundle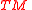 
.
A manifold is called parallelizable whenever admits a parallelization.
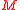is parallelizable iff there is a diffeomorphism 
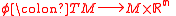such that the first projection of 
is 
and for each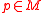 
the second factor—restricted to 
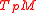—is a linear map 
.
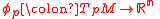In other words,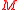
is parallelizable if and only if 
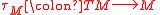is a trivial bundle
. For example suppose that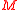
is an open subset of 
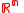, i.e., an open submanifold of 
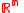. Then 
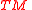is equal to 
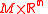, and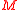 
is clearly parallelizable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a parallelization of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
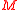of dimension n is a set of n global linearly independent vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.
Formal definition
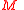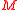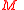Given a manifold of dimension n, a parallelization of is a set of n vector fields defined on all of such that for every 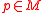the set is a basis of 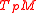, where 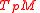denotes the fiber over of the tangent vector bundle 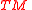.A manifold is called parallelizable whenever admits a parallelization.
Examples
- Every Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is a parallelizable manifold. - The product of parallelizable manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s is parallelizable.
Properties
Proposition. A manifold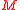 is parallelizable iff there is a diffeomorphism 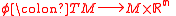such that the first projection of is and for each 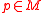the second factor—restricted to 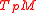—is a linear map 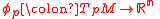.In other words,
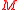is parallelizable if and only if 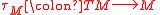is a trivial bundleBundle
Bundle or Bundling may refer to:In marketing:* Product bundling, a marketing strategy that involves offering several products for sale as one combined product...
. For example suppose that
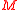is an open subset of 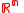, i.e., an open submanifold of 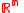. Then 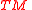is equal to 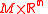, and is clearly parallelizable.See also
- Chart (topology)
- Differentiable manifoldDifferentiable manifoldA differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
- Frame bundleFrame bundleIn mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
- Orthonormal frame bundle
- Principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
- Connection (mathematics)Connection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- G-structureG-structureIn differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....