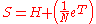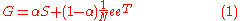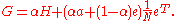Google matrix
Encyclopedia
A Google matrix is a particular stochastic matrix
that is used by Google
's PageRank
algorithm. The matrix represents a graph with edges representing links between pages.
The rank of each page can be generated iteratively from the Google matrix using the power method. However, in order for the power method to converge, the matrix must be stochastic, irreducible
and aperiodic.
Assuming there are n pages, we can fill out H by doing the following:
We can first generate the stochastic matrix S from H by adding an edge from every sink state to every other node. In the case where there is only one sink state the matrix S is written as:
to every other node. In the case where there is only one sink state the matrix S is written as:
where N is the number of nodes.
Then, by creating a relation between nodes without a relation with a factor of , the matrix will become irreducible. By making
, the matrix will become irreducible. By making  irreducible, we are also making it aperiodic.
irreducible, we are also making it aperiodic.
The final Google matrix G can be computed as:
By the construction the sum of all non-negative elements inside each matrix column is equal to unit.
If combined with the H computed above and with the assumption of a single sink node , the Google matrix can be written as:
, the Google matrix can be written as:
Although G is a dense matrix, it is computable using H which is a sparse matrix. Usually for modern directed networks the matrix H has only about ten nonzero elements in a line, thus only about 10N multiplications are needed to multiply a vector by matrix G[1,2].
An example of the matrix construction
construction
for Eq.(1) within a simple network is given in the article CheiRank
.
For the actual matrix, Google uses a damping factor around 0.85 [1,2,3]. The term
around 0.85 [1,2,3]. The term 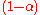 gives a surfer probability to jump randomly on any page. The matrix
gives a surfer probability to jump randomly on any page. The matrix  belongs to the class of Perron-Frobenius operators of Markov chains [1].
belongs to the class of Perron-Frobenius operators of Markov chains [1].
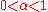 there is only one maximal eigenvalue
there is only one maximal eigenvalue
 with the corresponding right eigenvector
with the corresponding right eigenvector
which has non-negative elements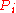 which can be viewed as
which can be viewed as
stationary probability distribution [1]. These probabilities
ordered by their decreasing values give the PageRank vector
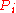 with the RageRank
with the RageRank 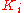 used
used
by Google search to rank webpages. Usually one has for the World Wide Web
that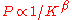
with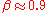 . The number of nodes with
. The number of nodes with
a given PageRank value scales as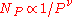
with the exponent [4,5].
[4,5].
The left eigenvector at has constant matrix elements.
has constant matrix elements.
With all eigenvalues move as
all eigenvalues move as
 except
except
the maximal eigenvalue , which remains unchanged [1].
, which remains unchanged [1].
The PageRank vector varies with but other eigenvectors
but other eigenvectors
with remain unchanged due to their orthogonality
remain unchanged due to their orthogonality
to the constant left vector at .
.
The gap between and other eigenvalue is
and other eigenvalue is
 gives a rapid convergence of a random initial vector to the PageRank approximately after 50 multiplications
gives a rapid convergence of a random initial vector to the PageRank approximately after 50 multiplications
on matrix.
matrix.
At the matrix
the matrix 
has generally many degenerate eigenvalues
(see e.g. [6,7]). An example of the eigenvalue spectrum of the Google matrix of various directed networks is shown in Fig.1 taken from [7].
The Google matrix can be also constructed for the Ulam networks generated by the Ulam method [8] for dynamical maps. The spectral properties of such matrices are discussed in [9,10,11,12,13,14]. In a number of cases the spectrum is described by the fractal Weyl law [10,12].
The Google matrix can be constructed also for other directed networks, e.g. for the procedure call network of the Linux Kernel software introduced in [15]. In this case the spectrum of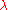 is described by the fractal Weyl law with the fractal dimension
is described by the fractal Weyl law with the fractal dimension  (see Fig.2 from [16]). Numerical analysis shows that the eigenstates of matrix
(see Fig.2 from [16]). Numerical analysis shows that the eigenstates of matrix  are localized (see Fig.3 from [16]). Arnoldi iteration
are localized (see Fig.3 from [16]). Arnoldi iteration
method allows to compute many eigenvalues and eigenvectors for matrices of rather large size [13,14,16].
Other examples of matrix include the Google matrix of brain [17]
matrix include the Google matrix of brain [17]
and business process management [18], see also [19].
and Larry Page
in 1998 [20], see also articles PageRank
and [21],[22].
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
that is used by Google
Google
Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...
's PageRank
PageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
algorithm. The matrix represents a graph with edges representing links between pages.
The rank of each page can be generated iteratively from the Google matrix using the power method. However, in order for the power method to converge, the matrix must be stochastic, irreducible
Irreducible (mathematics)
In mathematics, the concept of irreducibility is used in several ways.* In abstract algebra, irreducible can be an abbreviation for irreducible element; for example an irreducible polynomial....
and aperiodic.
H matrix
In order to generate the Google matrix, we must first generate a matrix H representing the relations between pages or nodes.Assuming there are n pages, we can fill out H by doing the following:
- Fill in each entry
 with a 1 if node
with a 1 if node 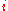 has a link to node
has a link to node 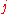 , and 0 otherwise; this is the adjacency matrix of links.
, and 0 otherwise; this is the adjacency matrix of links. - Divide each row by
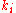 where
where 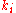 is the total number of links to other pages from node i. The matrix H is usually not stochastic, irreducible, or aperiodic, that makes it unsuitable for the PageRankPageRankPageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
is the total number of links to other pages from node i. The matrix H is usually not stochastic, irreducible, or aperiodic, that makes it unsuitable for the PageRankPageRankPageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
algorithm.
G matrix
Given H, we can generate G by making H stochastic, irreducible, and aperiodic.We can first generate the stochastic matrix S from H by adding an edge from every sink state
 to every other node. In the case where there is only one sink state the matrix S is written as:
to every other node. In the case where there is only one sink state the matrix S is written as:where N is the number of nodes.
Then, by creating a relation between nodes without a relation with a factor of
 , the matrix will become irreducible. By making
, the matrix will become irreducible. By making  irreducible, we are also making it aperiodic.
irreducible, we are also making it aperiodic.The final Google matrix G can be computed as:
By the construction the sum of all non-negative elements inside each matrix column is equal to unit.
If combined with the H computed above and with the assumption of a single sink node
 , the Google matrix can be written as:
, the Google matrix can be written as:Although G is a dense matrix, it is computable using H which is a sparse matrix. Usually for modern directed networks the matrix H has only about ten nonzero elements in a line, thus only about 10N multiplications are needed to multiply a vector by matrix G[1,2].
An example of the matrix
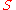 construction
constructionfor Eq.(1) within a simple network is given in the article CheiRank
CheiRank
The CheiRank is an eigenvector with a maximal real eigenvalue of the Google matrix G^* constructed for a directed network with the inverted directions of links. It is similar to the PageRank vector, which ranks the network nodes in average proportionally to a number of incoming links being the...
.
For the actual matrix, Google uses a damping factor
 around 0.85 [1,2,3]. The term
around 0.85 [1,2,3]. The term 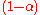 gives a surfer probability to jump randomly on any page. The matrix
gives a surfer probability to jump randomly on any page. The matrix  belongs to the class of Perron-Frobenius operators of Markov chains [1].
belongs to the class of Perron-Frobenius operators of Markov chains [1].Spectrum and eigenstates of G matrix
For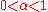 there is only one maximal eigenvalue
there is only one maximal eigenvalue with the corresponding right eigenvector
with the corresponding right eigenvectorwhich has non-negative elements
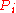 which can be viewed as
which can be viewed asstationary probability distribution [1]. These probabilities
ordered by their decreasing values give the PageRank vector
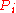 with the RageRank
with the RageRank 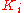 used
usedby Google search to rank webpages. Usually one has for the World Wide Web
that
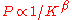
with
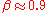 . The number of nodes with
. The number of nodes witha given PageRank value scales as
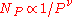
with the exponent
 [4,5].
[4,5].The left eigenvector at
 has constant matrix elements.
has constant matrix elements.With
 all eigenvalues move as
all eigenvalues move as except
exceptthe maximal eigenvalue
 , which remains unchanged [1].
, which remains unchanged [1].The PageRank vector varies with
 but other eigenvectors
but other eigenvectorswith
 remain unchanged due to their orthogonality
remain unchanged due to their orthogonalityto the constant left vector at
 .
.The gap between
 and other eigenvalue is
and other eigenvalue is gives a rapid convergence of a random initial vector to the PageRank approximately after 50 multiplications
gives a rapid convergence of a random initial vector to the PageRank approximately after 50 multiplicationson
 matrix.
matrix.At
 the matrix
the matrix 
has generally many degenerate eigenvalues

(see e.g. [6,7]). An example of the eigenvalue spectrum of the Google matrix of various directed networks is shown in Fig.1 taken from [7].
The Google matrix can be also constructed for the Ulam networks generated by the Ulam method [8] for dynamical maps. The spectral properties of such matrices are discussed in [9,10,11,12,13,14]. In a number of cases the spectrum is described by the fractal Weyl law [10,12].
The Google matrix can be constructed also for other directed networks, e.g. for the procedure call network of the Linux Kernel software introduced in [15]. In this case the spectrum of
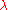 is described by the fractal Weyl law with the fractal dimension
is described by the fractal Weyl law with the fractal dimension  (see Fig.2 from [16]). Numerical analysis shows that the eigenstates of matrix
(see Fig.2 from [16]). Numerical analysis shows that the eigenstates of matrix  are localized (see Fig.3 from [16]). Arnoldi iteration
are localized (see Fig.3 from [16]). Arnoldi iterationArnoldi iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
method allows to compute many eigenvalues and eigenvectors for matrices of rather large size [13,14,16].
Other examples of
 matrix include the Google matrix of brain [17]
matrix include the Google matrix of brain [17]and business process management [18], see also [19].
Historical notes
The Google matrix with damping factor was described by Sergey BrinSergey Brin
Sergey Mikhaylovich Brin is a Russian-born American computer scientist and internet entrepreneur who, with Larry Page, co-founded Google, one of the largest internet companies. , his personal wealth is estimated to be $16.7 billion....
and Larry Page
Larry Page
Lawrence "Larry" Page is an American computer scientist and internet entrepreneur who, with Sergey Brin, is best known as the co-founder of Google. As of April 4, 2011, he is also the chief executive of Google, as announced on January 20, 2011...
in 1998 [20], see also articles PageRank
PageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
and [21],[22].
See also
- PageRankPageRankPageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
, CheiRankCheiRankThe CheiRank is an eigenvector with a maximal real eigenvalue of the Google matrix G^* constructed for a directed network with the inverted directions of links. It is similar to the PageRank vector, which ranks the network nodes in average proportionally to a number of incoming links being the... - Arnoldi iterationArnoldi iterationIn numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
- Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, Transfer operatorTransfer operatorIn mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
, Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of... - Web search engines