P-adically closed field
Encyclopedia
In mathematics
, a p-adically closed field is a field
that enjoys a closure property that is a close analogue for p-adic fields
to what real closure
is to the real field
. They were introduced by James Ax
and Simon B. Kochen
in 1965.
valuation (with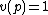
). If F is a (not necessarily algebraic) extension field
of K, itself equipped with a valuation w, we say that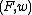
is formally p-adic when the following conditions are satisfied:
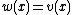for all x in K),
the residue field
of w coincides with the residue field of v (the residue field being the quotient of the valuation ring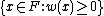 
by its maximal ideal 
),
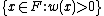the smallest positive value of w coincides with the smallest positive value of v (namely 1, since v was assumed to be normalized): in other words, a uniformizer for K remains a uniformizer for F.
(Note that the value group of K may be larger than that of F since it may contain infinitely large elements over the latter.)
The formally p-adic fields can be viewed as an analogue of the formally real fields.
For example, the field ℚ(i) of Gaussian rational
s, if equipped with the valuation w given by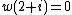
(and 
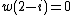) is formally 5-adic (the place v=5 of the rationals splits in two places of the Gaussian rationals since 
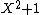factors over the residue field with 5 elements, and w is one of these places). The field of 5-adic numbers (which contains both the rationals and the Gaussian rationals embedded as per the place w) is also formally 5-adic. On the other hand, the field of Gaussian rationals is not formally 3-adic for any valuation, because the only valuation w on it which extends the 3-adic valuation is given by 
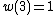and its residue field has 9 elements.
When F is formally p-adic but that there does not exist any proper algebraic formally p-adic extension of F, then F is said to be p-adically closed. For example, the field of p-adic numbers is p-adically closed, and so is the algebraic closure of the rationals inside it (the field of p-adic algebraic numbers).
If F is p-adically closed, then:
The first statement is an analogue of the fact that the order of a real-closed field is uniquely determined by the algebraic structure.
The definitions given above can be copied to a more general context: if K is a field equipped with a valuation v such that
(these hypotheses are satisfied for the field of rationals, with q=π=p the prime number having valuation 1) then we can speak of formally v-adic fields (or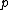
-adic if 
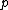is the ideal corresponding to v) and v-adically complete fields.
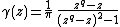
(when
). It is easy to check that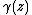 
always has non-negative valuation. The Kochen operator can be thought of as a p-adic (or v-adic) analogue of the square function in the real case.
An extension field F of K is formally v-adic if and only if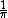
does not belong to the subring generated over the value ring of K by the image of the Kochen operator on F. This is an analogue of the statement (or definition) that a field is formally real when 
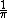is not a sum of squares.
and model complete
, and if we slightly enrich the language it admits quantifier elimination
. Thus, one can define p-adically closed fields as those whose first-order theory is elementarily equivalent to that of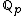
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a p-adically closed field is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
that enjoys a closure property that is a close analogue for p-adic fields
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
to what real closure
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
is to the real field
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. They were introduced by James Ax
James Ax
James Burton Ax was a mathematician who proved several results in algebra and number theory by using model theory. He shared the seventh Frank Nelson Cole Prize in Number Theory with Simon B. Kochen, which was awarded for a series of three joint papers on Diophantine problems.James Ax earned his...
and Simon B. Kochen
Simon B. Kochen
Simon Bernhard Kochen is an American mathematician, working in the fields of model theory, number theory and quantum mechanics....
in 1965.
Definition
Let K be the field ℚ of rational numbers and v be its usual p-adicP-adic order
In number theory, for a given prime number p, the p-adic order or additive p-adic valuation of a number n is the highest exponent ν such that pν divides n. It is commonly abbreviated νp. The most important application of the p-adic order is in constructing the field of p-adic numbers...
valuation (with
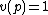). If F is a (not necessarily algebraic) extension fieldField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of K, itself equipped with a valuation w, we say that
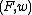is formally p-adic when the following conditions are satisfied:
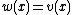for all x in K),
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
of
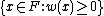by its maximal ideal ),
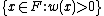(Note that the value group of K may be larger than that of F since it may contain infinitely large elements over the latter.)
The formally p-adic fields can be viewed as an analogue of the formally real fields.
For example, the field ℚ(i) of Gaussian rational
Gaussian rational
In mathematics, a Gaussian rational number is a complex number of the form p + qi, where p and q are both rational numbers....
s, if equipped with the valuation w given by
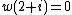(and 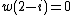) is formally 5-adic (the place v=5 of the rationals splits in two places of the Gaussian rationals since 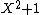factors over the residue field with 5 elements, and w is one of these places). The field of 5-adic numbers (which contains both the rationals and the Gaussian rationals embedded as per the place w) is also formally 5-adic. On the other hand, the field of Gaussian rationals is not formally 3-adic for any valuation, because the only valuation w on it which extends the 3-adic valuation is given by 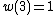and its residue field has 9 elements.When F is formally p-adic but that there does not exist any proper algebraic formally p-adic extension of F, then F is said to be p-adically closed. For example, the field of p-adic numbers is p-adically closed, and so is the algebraic closure of the rationals inside it (the field of p-adic algebraic numbers).
If F is p-adically closed, then:
- there is a unique valuation w on F which makes F p-adically closed (so it is legitimate to say that F, rather than the pair
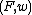, is p-adically closed), - F is HenselianHenselian ringIn mathematics, a Henselian ring is a local ring in which Hensel's lemma holds. They were defined by , who named them after Kurt Hensel.Some standard references for Hensel rings are , , and .-Definitions:...
with respect to this place (that is, its valuation ring is so), - the valuation ring of F is exactly the image of the Kochen operator (see below),
- the value group of F is an extension by ℤ (the value group of K) of a divisible group, with the lexicographical orderLexicographical orderIn mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
.
The first statement is an analogue of the fact that the order of a real-closed field is uniquely determined by the algebraic structure.
The definitions given above can be copied to a more general context: if K is a field equipped with a valuation v such that
- the residue field of K is finite (call q its cardinal and p its characteristic),
- the value group of v admits a smallest positive element (call it 1, and say π is a uniformizer, i.e.
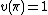), - K has finite absolute ramification, i.e.,
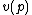is finite (that is, a finite multiple of 
),
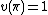(these hypotheses are satisfied for the field of rationals, with q=π=p the prime number having valuation 1) then we can speak of formally v-adic fields (or
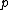-adic if 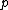is the ideal corresponding to v) and v-adically complete fields.The Kochen operator
If K is a field equipped with a valuation v satisfying the hypothesis and with the notations introduced in the previous paragraph, define the Kochen operator by: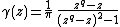(when
). It is easy to check that 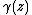always has non-negative valuation. The Kochen operator can be thought of as a p-adic (or v-adic) analogue of the square function in the real case.An extension field F of K is formally v-adic if and only if
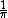does not belong to the subring generated over the value ring of K by the image of the Kochen operator on F. This is an analogue of the statement (or definition) that a field is formally real when 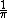is not a sum of squares.First-order theory
The first-order theory of p-adically closed fields (here we are restricting ourselves to the p-adic case, i.e., K is the field of rationals and v is the p-adic valuation) is completeComplete theory
In mathematical logic, a theory is complete if it is a maximal consistent set of sentences, i.e., if it is consistent, and none of its proper extensions is consistent...
and model complete
Model complete theory
In model theory, a first-order theory is called model complete if every embedding of models is an elementary embedding.Equivalently, every first-order formula is equivalent to a universal formula.This notion was introduced by Abraham Robinson....
, and if we slightly enrich the language it admits quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
. Thus, one can define p-adically closed fields as those whose first-order theory is elementarily equivalent to that of
.
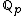