P-adic order
Encyclopedia
In number theory
, for a given prime number
p, the p-adic order or additive p-adic valuation of a number n is the highest exponent ν such that pν divides n. It is commonly abbreviated νp(n). The most important application of the p-adic order is in constructing the field of p-adic numbers
. It is also applied toward various more elementary topics, such as the distinction between singly and doubly even numbers.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, for a given prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, the p-adic order or additive p-adic valuation of a number n is the highest exponent ν such that pν divides n. It is commonly abbreviated νp(n). The most important application of the p-adic order is in constructing the field of p-adic numbers
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
. It is also applied toward various more elementary topics, such as the distinction between singly and doubly even numbers.
Properties
-
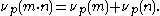
-
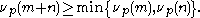 Moreover, if
Moreover, if  , then
, then