
Ordinal collapsing function
Encyclopedia
In mathematical logic
and set theory
, an ordinal collapsing function (or projection function) is a technique for defining (notations
for) certain recursive
large countable ordinal
s, whose principle is to give names to certain ordinals much larger than the one being defined, perhaps even large cardinals
(though they can be replaced with recursively large ordinals at the cost of extra technical difficulty), and then “collapse” them down to a system of notations for the sought-after ordinal. For this reason, ordinal collapsing functions are described as an impredicative manner of naming ordinals.
The details of the definition of ordinal collapsing functions vary, and get more complicated as greater ordinals are being defined, but the typical idea is that whenever the notation system “runs out of fuel” and cannot name a certain ordinal, a much larger ordinal is brought “from above” to give a name to that critical point. An example of how this works will be detailed below, for an ordinal collapsing function defining the Bachmann-Howard ordinal (i.e., defining a system of notations up to the Bachmann-Howard ordinal).
The use and definition of ordinal collapsing functions is inextricably intertwined with the theory of ordinal analysis
, since the large countable ordinals defined and denoted by a given collapse are used to describe the ordinal-theoretic strength of certain formal systems, typically subsystems of analysis
(such as those seen in the light of reverse mathematics
), extensions of Kripke-Platek set theory, Bishop
-style systems of constructive mathematics
or Martin-Löf
-style systems of intuitionistic type theory
.
Ordinal collapsing functions are typically denoted using some variation of the Greek letter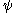 (psi
(psi
).
 stand for the first uncountable ordinal
stand for the first uncountable ordinal
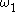 , or, in fact, any ordinal which is (an
, or, in fact, any ordinal which is (an  -number and) guaranteed to be greater than all the countable ordinals which will be constructed (for example, the Church-Kleene ordinal is adequate for our purposes; but we will work with
-number and) guaranteed to be greater than all the countable ordinals which will be constructed (for example, the Church-Kleene ordinal is adequate for our purposes; but we will work with  because it allows the convenient use of the word countable in the definitions).
because it allows the convenient use of the word countable in the definitions).
We define a function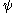 (which will be non-decreasing
(which will be non-decreasing
and continuous
), taking an arbitrary ordinal to a countable ordinal
to a countable ordinal 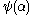 , recursively on
, recursively on  , as follows:
, as follows:
In a more concise (although more obscure) way: is the smallest ordinal which cannot be expressed from
is the smallest ordinal which cannot be expressed from 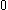 ,
, 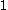 ,
, 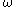 and
and  using sums, products, exponentials, and the
using sums, products, exponentials, and the 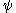 function itself (to previously constructed ordinals less than
function itself (to previously constructed ordinals less than  ).
).
Here is an attempt to explain the motivation for the definition of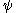 in intuitive terms: since the usual operations of addition, multiplication and exponentiation are not sufficient to designate ordinals very far, we attempt to systematically create new names for ordinals by taking the first one which does not have a name yet, and whenever we run out of names, rather than invent them in an ad hoc fashion or using diagonal schemes, we seek them in the ordinals far beyond the ones we are constructing (beyond
in intuitive terms: since the usual operations of addition, multiplication and exponentiation are not sufficient to designate ordinals very far, we attempt to systematically create new names for ordinals by taking the first one which does not have a name yet, and whenever we run out of names, rather than invent them in an ad hoc fashion or using diagonal schemes, we seek them in the ordinals far beyond the ones we are constructing (beyond 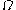 , that is); so we give names to uncountable ordinals and, since in the end the list of names is necessarily countable,
, that is); so we give names to uncountable ordinals and, since in the end the list of names is necessarily countable, 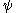 will “collapse” them to countable ordinals.
will “collapse” them to countable ordinals.
Computation of values of
To clarify how the function 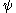 is able to produce notations for certain ordinals, we now compute its first values.
is able to produce notations for certain ordinals, we now compute its first values.
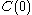 . It contains ordinals
. It contains ordinals  ,
,  ,
,  ,
, 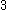 ,
,  ,
,  ,
, 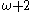 ,
, 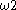 ,
, 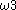 ,
, 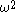 ,
, 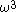 ,
, 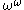 ,
,  and so on. It also contains such ordinals as
and so on. It also contains such ordinals as  ,
,  ,
, 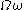 ,
, 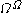 . The first ordinal which it does not contain is
. The first ordinal which it does not contain is 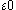
(which is the limit of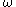 ,
,  ,
, 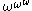 and so on — less than
and so on — less than  by assumption). The upper bound of the ordinals it contains is
by assumption). The upper bound of the ordinals it contains is  (the limit of
(the limit of 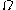 ,
,  ,
, 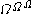 and so on), but that is not so important. This shows that
and so on), but that is not so important. This shows that 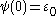 .
.
Similarly,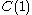 contains the ordinals which can be formed from
contains the ordinals which can be formed from 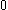 ,
, 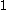 ,
, 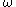 ,
, 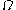 and this time also
and this time also  , using addition, multiplication and exponentiation. This contains all the ordinals up to
, using addition, multiplication and exponentiation. This contains all the ordinals up to 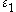 but not the latter, so
but not the latter, so 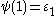 . In this manner, we prove that
. In this manner, we prove that 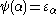 inductively on
inductively on  : the proof works, however, only as long as
: the proof works, however, only as long as 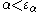 . We therefore have:
. We therefore have:
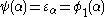 for all
for all 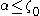 , where
, where 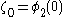 is the smallest fixed point of
is the smallest fixed point of  .
.
(Here, the functions are the Veblen function
functions are the Veblen function
s defined starting with .)
.)
Now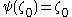 but
but 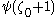 is no larger, since
is no larger, since 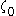 cannot be constructed using finite applications of
cannot be constructed using finite applications of 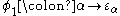 and thus never belongs to a
and thus never belongs to a 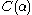 set for
set for 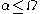 , and the function
, and the function  remains “stuck” at
remains “stuck” at 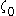 for some time:
for some time:
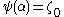 for all
for all 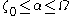 .
.
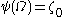 . However, when we come to computing
. However, when we come to computing  , something has changed: since
, something has changed: since 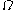 was (“artificially”) added to all the
was (“artificially”) added to all the  , we are permitted to take the value
, we are permitted to take the value 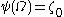 in the process. So
in the process. So 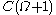 contains all ordinals which can be built from
contains all ordinals which can be built from 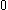 ,
, 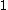 ,
,  ,
, 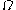 , the
, the 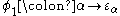 function up to
function up to 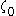 and this time also
and this time also 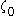 itself, using addition, multiplication and exponentiation. The smallest ordinal not in
itself, using addition, multiplication and exponentiation. The smallest ordinal not in 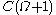 is
is  (the smallest
(the smallest  -number after
-number after 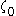 ).
).
We say that the definition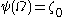 and the next values of the function
and the next values of the function 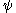 such as
such as 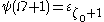 are impredicative because they use ordinals (here,
are impredicative because they use ordinals (here, 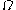 ) greater than the ones which are being defined (here,
) greater than the ones which are being defined (here, 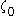 ).
).
Values of
The fact that 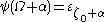 remains true for all
remains true for all 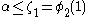 (note, in particular, that
(note, in particular, that 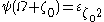 : but since now the ordinal
: but since now the ordinal 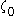 has been constructed there is nothing to prevent from going beyond this). However, at
has been constructed there is nothing to prevent from going beyond this). However, at 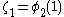 (the first fixed point of
(the first fixed point of 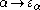 beyond
beyond 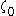 ), the construction stops again, because
), the construction stops again, because  cannot be constructed from smaller ordinals and
cannot be constructed from smaller ordinals and 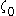 by finitely applying the
by finitely applying the  function. So we have
function. So we have 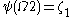 .
.
The same reasoning shows that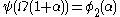 for all
for all 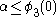 , where
, where  enumerates the fixed points of
enumerates the fixed points of 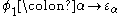 and
and 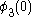 is the first fixed point of
is the first fixed point of  . We then have
. We then have 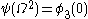 .
.
Again, we can see that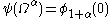 for some time: this remains true until the first fixed point
for some time: this remains true until the first fixed point 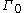 of
of 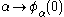 , which is the Feferman-Schütte ordinal. Thus,
, which is the Feferman-Schütte ordinal. Thus, 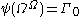 is the Feferman-Schütte ordinal.
is the Feferman-Schütte ordinal.
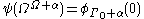 for all
for all 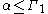 where
where 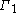 is the next fixed point of
is the next fixed point of 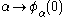 . So, if
. So, if 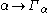 enumerates the fixed points in question. (which can also be noted
enumerates the fixed points in question. (which can also be noted 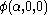 using the many-valued Veblen functions) we have
using the many-valued Veblen functions) we have 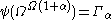 , until the first fixed point of the
, until the first fixed point of the 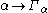 itself, which will be
itself, which will be 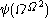 . In this manner:
. In this manner:
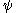 function defines notations for ordinals up to the Bachmann-Howard ordinal.
function defines notations for ordinals up to the Bachmann-Howard ordinal.
 is an ordinal which is a power of
is an ordinal which is a power of  (for example
(for example 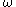 itself, or
itself, or 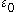 , or
, or 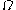 ), any ordinal
), any ordinal  can be uniquely expressed in the form
can be uniquely expressed in the form 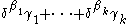 , where
, where 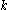 is a natural number,
is a natural number, 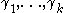 are non-zero ordinals less than
are non-zero ordinals less than 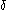 , and
, and 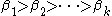 are ordinal numbers (we allow
are ordinal numbers (we allow 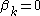 ). This “base
). This “base 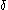 representation” is an obvious generalization of the Cantor normal form (which is the case
representation” is an obvious generalization of the Cantor normal form (which is the case 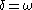 ). Of course, it may quite well be that the expression is uninteresting, i.e.,
). Of course, it may quite well be that the expression is uninteresting, i.e., 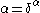 , but in any other case the
, but in any other case the 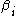 must all be less than
must all be less than  ; it may also be the case that the expression is trivial (i.e.,
; it may also be the case that the expression is trivial (i.e., 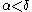 , in which case
, in which case 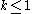 and
and 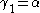 ).
).
If is an ordinal less than
is an ordinal less than 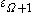 , then its base
, then its base 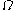 representation has coefficients
representation has coefficients 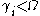 (by definition) and exponents
(by definition) and exponents  (because of the assumption
(because of the assumption 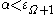 ): hence one can rewrite these exponents in base
): hence one can rewrite these exponents in base 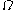 and repeat the operation until the process terminates (any decreasing sequence of ordinals is finite). We call the resulting expression the iterated base
and repeat the operation until the process terminates (any decreasing sequence of ordinals is finite). We call the resulting expression the iterated base 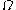 representation of
representation of  and the various coefficients involved (including as exponents) the pieces of the representation (they are all
and the various coefficients involved (including as exponents) the pieces of the representation (they are all 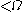 ), or, for short, the
), or, for short, the  -pieces of
-pieces of  .
.
Some properties of
 less than the Bachmann-Howard ordinal. We do this by induction on
less than the Bachmann-Howard ordinal. We do this by induction on 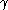 .
.
If is less than
is less than 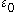 , we use the iterated Cantor normal form of
, we use the iterated Cantor normal form of  . Otherwise, there exists a largest
. Otherwise, there exists a largest  -number
-number 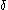 less or equal to
less or equal to  (this is because the set of
(this is because the set of  -numbers is closed): if
-numbers is closed): if  then by induction we have defined a notation for
then by induction we have defined a notation for 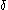 and the base
and the base 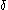 representation of
representation of 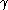 gives one for
gives one for 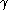 , so we are finished.
, so we are finished.
It remains to deal with the case where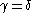 is an
is an  -number: we have argued that, in this case, we can write
-number: we have argued that, in this case, we can write 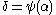 for some (possibly uncountable) ordinal
for some (possibly uncountable) ordinal 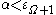 : let
: let  be the greatest possible such ordinal (which exists since
be the greatest possible such ordinal (which exists since 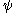 is continuous). We use the iterated base
is continuous). We use the iterated base 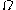 representation of
representation of  : it remains to show that every piece of this representation is less than
: it remains to show that every piece of this representation is less than 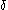 (so we have already defined a notation for it). If this is not the case then, by the properties we have shown,
(so we have already defined a notation for it). If this is not the case then, by the properties we have shown, 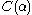 does not contain
does not contain  ; but then
; but then 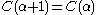 (they are closed under the same operations, since the value of
(they are closed under the same operations, since the value of 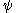 at
at  can never be taken), so
can never be taken), so 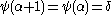 , contradicting the maximality of
, contradicting the maximality of  .
.
Note: Actually, we have defined canonical notations not just for ordinals below the Bachmann-Howard ordinal but also for certain uncountable ordinals, namely those whose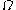 -pieces are less than the Bachmann-Howard ordinal (viz.: write them in iterated base
-pieces are less than the Bachmann-Howard ordinal (viz.: write them in iterated base  representation and use the canonical representation for every piece). This canonical notation is used for arguments of the
representation and use the canonical representation for every piece). This canonical notation is used for arguments of the 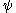 function (which may be uncountable).
function (which may be uncountable).
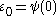 , the canonical ordinal notation defined coincides with the iterated Cantor normal form (by definition).
, the canonical ordinal notation defined coincides with the iterated Cantor normal form (by definition).
For ordinals less than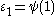 , the notation coincides with iterated base
, the notation coincides with iterated base 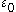 notation (the pieces being themselves written in iterated Cantor normal form): e.g.,
notation (the pieces being themselves written in iterated Cantor normal form): e.g., 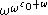 will be written
will be written  , or, more accurately,
, or, more accurately, 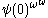 . For ordinals less than
. For ordinals less than 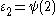 , we similarly write in iterated base
, we similarly write in iterated base 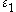 and then write the pieces in iterated base
and then write the pieces in iterated base 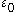 (and write the pieces of that in iterated Cantor normal form): so
(and write the pieces of that in iterated Cantor normal form): so 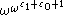 is written
is written 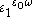 , or, more accurately,
, or, more accurately, 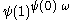 . Thus, up to
. Thus, up to  , we always use the largest possible
, we always use the largest possible  -number base which gives a non-trivial representation.
-number base which gives a non-trivial representation.
Beyond this, we may need to express ordinals beyond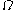 : this is always done in iterated
: this is always done in iterated 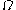 -base, and the pieces themselves need to be expressed using the largest possible
-base, and the pieces themselves need to be expressed using the largest possible  -number base which gives a non-trivial representation.
-number base which gives a non-trivial representation.
Note that while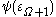 is equal to the Bachmann-Howard ordinal, this is not a “canonical notation” in the sense we have defined (canonical notations are defined only for ordinals less than the Bachmann-Howard ordinal).
is equal to the Bachmann-Howard ordinal, this is not a “canonical notation” in the sense we have defined (canonical notations are defined only for ordinals less than the Bachmann-Howard ordinal).
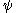 functions, the arguments of the “inner”
functions, the arguments of the “inner” 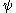 function are always less than those of the “outer” one (this is a consequence of the fact that the
function are always less than those of the “outer” one (this is a consequence of the fact that the 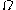 -pieces of
-pieces of  , where
, where  is the largest possible such that
is the largest possible such that 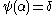 for some
for some  -number
-number 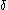 , are all less than
, are all less than 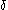 , as we have shown above). For example,
, as we have shown above). For example, 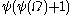 does not occur as a notation: it is a well-defined expression (and it is equal to
does not occur as a notation: it is a well-defined expression (and it is equal to  since
since 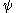 is constant between
is constant between 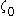 and
and  ), but it is not a notation produced by the inductive algorithm we have outlined.
), but it is not a notation produced by the inductive algorithm we have outlined.
Canonicalness can be checked recursively: an expression is canonical if and only if it is either the iterated Cantor normal form of an ordinal less than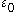 , or an iterated base
, or an iterated base 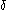 representation all of whose pieces are canonical, for some
representation all of whose pieces are canonical, for some  where
where  is itself written in iterated base
is itself written in iterated base 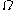 representation all of whose pieces are canonical and less than
representation all of whose pieces are canonical and less than 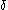 . The order is checked by lexicographic verification at all levels (keeping in mind that
. The order is checked by lexicographic verification at all levels (keeping in mind that 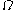 is greater than any expression obtained by
is greater than any expression obtained by 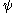 , and for canonical values the greater
, and for canonical values the greater 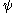 always trumps the lesser or even arbitrary sums, products and exponentials of the lesser).
always trumps the lesser or even arbitrary sums, products and exponentials of the lesser).
For example, is a canonical notation for an ordinal which is less than the Feferman-Schütte ordinal: it can be written using the Veblen functions as
is a canonical notation for an ordinal which is less than the Feferman-Schütte ordinal: it can be written using the Veblen functions as 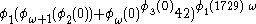 .
.
Concerning the order, one might point out that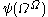 (the Feferman-Schütte ordinal) is much more than
(the Feferman-Schütte ordinal) is much more than 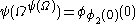 (because
(because 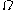 is greater than
is greater than  of anything), and
of anything), and 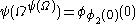 is itself much more than
is itself much more than 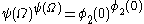 (because
(because 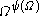 is greater than
is greater than 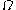 , so any sum-product-or-exponential expression involving
, so any sum-product-or-exponential expression involving 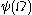 and smaller value will remain less than
and smaller value will remain less than 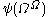 ). In fact,
). In fact,  is already less than
is already less than 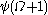 .
.
), we might define standard sequences converging to any one of them (provided it is a limit ordinal, of course). Actually we will define canonical sequences for certain uncountable ordinals, too, namely the uncountable ordinals of countable cofinality (if we are to hope to define a sequence converging to them…) which are representable (that is, all of whose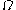 -pieces are less than the Bachmann-Howard ordinal).
-pieces are less than the Bachmann-Howard ordinal).
The following rules are more or less obvious, except for the last:
Here are some examples for the last (and most interesting) case:
Here are some examples of the other cases:
Even though the Bachmann-Howard ordinal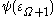 itself has no canonical notation, it is also useful to define a canonical sequence for it: this is
itself has no canonical notation, it is also useful to define a canonical sequence for it: this is 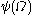 ,
, 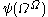 ,
, 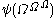 …
…
Then it is true that this process always terminates (as any decreasing sequence of ordinals is finite); however, like (but even more so than for) the hydra game
:
To give some flavor of what the process feels like, here are some steps of it: starting from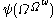 (the small Veblen ordinal), we might go down to
(the small Veblen ordinal), we might go down to 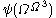 , from there down to
, from there down to 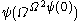 , then
, then  then
then 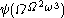 then
then 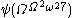 then
then 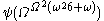 then
then  then
then 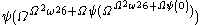 and so on. It appears as though the expressions are getting more and more complicated whereas, in fact, the ordinals always decrease.
and so on. It appears as though the expressions are getting more and more complicated whereas, in fact, the ordinals always decrease.
Concerning the first statement, one could introduce, for any ordinal less or equal to the Bachmann-Howard ordinal
less or equal to the Bachmann-Howard ordinal 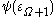 , the integer function
, the integer function 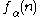 which counts the number of steps of the process before termination if one always selects the
which counts the number of steps of the process before termination if one always selects the  'th element from the canonical sequence. Then
'th element from the canonical sequence. Then 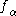 can be a very fast growing function: already
can be a very fast growing function: already 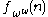 is essentially
is essentially  , the function
, the function 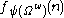 is comparable with the Ackermann function
is comparable with the Ackermann function
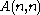 , and
, and 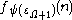 is quite unimaginable.
is quite unimaginable.
Concerning the second statement, a precise version is given by ordinal analysis
: for example, Kripke-Platek set theory can prove that the process terminates for any given less than the Bachmann-Howard ordinal, but it cannot do this uniformly, i.e., it cannot prove the termination starting from the Bachmann-Howard ordinal. Some theories like Peano arithmetic are limited by much smaller ordinals (
less than the Bachmann-Howard ordinal, but it cannot do this uniformly, i.e., it cannot prove the termination starting from the Bachmann-Howard ordinal. Some theories like Peano arithmetic are limited by much smaller ordinals (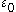 in the case of Peano arithmetic).
in the case of Peano arithmetic).
 less powerful.
less powerful.
If we alter the definition of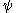 above to omit exponentiation from the repertoire from which
above to omit exponentiation from the repertoire from which 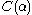 is constructed, then we get
is constructed, then we get 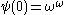 (as this is the smallest ordinal which cannot be constructed from
(as this is the smallest ordinal which cannot be constructed from 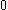 ,
, 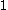 and
and 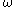 using addition and multiplication only), then
using addition and multiplication only), then 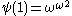 and similarly
and similarly 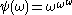 ,
,  until we come to a fixed point which is then our
until we come to a fixed point which is then our 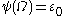 . We then have
. We then have 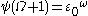 and so on until
and so on until 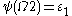 . Since multiplication of
. Since multiplication of 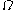 's is permitted, we can still form
's is permitted, we can still form 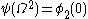 and
and 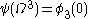 and so on, but our construction ends there as there is no way to get at or beyond
and so on, but our construction ends there as there is no way to get at or beyond 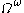 : so the range of this weakened system of notation is
: so the range of this weakened system of notation is 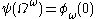 (the value of
(the value of  is the same in our weaker system as in our original system, except that now we cannot go beyond it). This does not even go as far as the Feferman-Schütte ordinal.
is the same in our weaker system as in our original system, except that now we cannot go beyond it). This does not even go as far as the Feferman-Schütte ordinal.
If we alter the definition of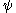 yet some more to allow only addition as a primitive for construction, we get
yet some more to allow only addition as a primitive for construction, we get 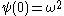 and
and 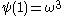 and so on until
and so on until 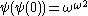 and still
and still  . This time,
. This time, 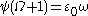 and so on until
and so on until  and similarly
and similarly  . But this time we can go no further: since we can only add
. But this time we can go no further: since we can only add 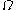 's, the range of our system is
's, the range of our system is 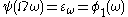 .
.
In both cases, we find that the limitation on the weakened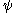 function comes not so much from the operations allowed on the countable ordinals as on the uncountable ordinals we allow ourselves to denote.
function comes not so much from the operations allowed on the countable ordinals as on the uncountable ordinals we allow ourselves to denote.
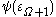 is the Bachmann-Howard ordinal. The reason why
is the Bachmann-Howard ordinal. The reason why 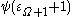 is no larger, with our definitions, is that there is no notation for
is no larger, with our definitions, is that there is no notation for 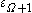 (it does not belong to
(it does not belong to 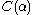 for any
for any  , it is always the least upper bound of it). One could try to add the
, it is always the least upper bound of it). One could try to add the  function (or the Veblen functions of so-many-variables) to the allowed primitives beyond addition, multiplication and exponentiation, but that does not get us very far. To create more systematic notations for countable ordinals, we need more systematic notations for uncountable ordinals: we cannot use the
function (or the Veblen functions of so-many-variables) to the allowed primitives beyond addition, multiplication and exponentiation, but that does not get us very far. To create more systematic notations for countable ordinals, we need more systematic notations for uncountable ordinals: we cannot use the 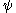 function itself because it only yields countable ordinals (e.g.,
function itself because it only yields countable ordinals (e.g., 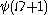 is,
is, 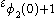 , certainly not
, certainly not  ), so the idea is to mimic its definition as follows:
), so the idea is to mimic its definition as follows:
Here,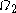 is a new ordinal guaranteed to be greater than all the ordinals which will be constructed using
is a new ordinal guaranteed to be greater than all the ordinals which will be constructed using 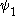 : again, letting
: again, letting 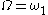 and
and  works.
works.
For example,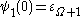 , and more generally
, and more generally 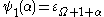 for all countable ordinals and even beyond (
for all countable ordinals and even beyond (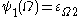 and
and 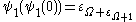 ): this holds up to the first fixed point
): this holds up to the first fixed point 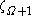 beyond
beyond 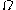 of the
of the 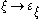 function, which is the limit of
function, which is the limit of 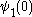 ,
, 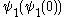 and so forth. Beyond this, we have
and so forth. Beyond this, we have 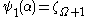 and this remains true until
and this remains true until 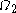 : exactly as was the case for
: exactly as was the case for 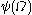 , we have
, we have 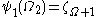 and
and 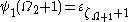 .
.
The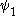 function gives us a system of notations (assuming we can somehow write down all countable ordinals!) for the uncountable ordinals below
function gives us a system of notations (assuming we can somehow write down all countable ordinals!) for the uncountable ordinals below 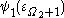 , which is the limit of
, which is the limit of 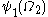 ,
, 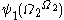 and so forth.
and so forth.
Now we can reinject these notations in the original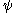 function, modified as follows:
function, modified as follows: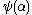 is the smallest ordinal which cannot be expressed from
is the smallest ordinal which cannot be expressed from  ,
,  ,
,  ,
, 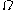 and
and  using sums, products, exponentials, the
using sums, products, exponentials, the  function, and the
function, and the 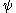 function itself (to previously constructed ordinals less than
function itself (to previously constructed ordinals less than  ).
).
This modified function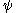 coincides with the previous one up to (and including)
coincides with the previous one up to (and including) 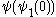 — which is the Bachmann-Howard ordinal. But now we can get beyond this, and
— which is the Bachmann-Howard ordinal. But now we can get beyond this, and 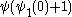 is
is 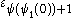 (the next
(the next  -number after the Bachmann-Howard ordinal). We have made our system doubly impredicative: to create notations for countable ordinals we use notations for certain ordinals between
-number after the Bachmann-Howard ordinal). We have made our system doubly impredicative: to create notations for countable ordinals we use notations for certain ordinals between 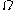 and
and 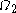 which are themselves defined using certain ordinals beyond
which are themselves defined using certain ordinals beyond 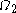 .
.
A variation on this scheme, which makes little difference when using just two (or finitely many) collapsing functions, but becomes important for infinitely many of them, is to define is the smallest ordinal which cannot be expressed from
is the smallest ordinal which cannot be expressed from  ,
, 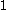 ,
, 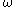 ,
, 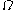 and
and 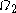 using sums, products, exponentials, and the
using sums, products, exponentials, and the 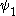 and
and 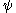 function (to previously constructed ordinals less than
function (to previously constructed ordinals less than  ).
).
i.e., allow the use of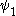 only for arguments less than
only for arguments less than  itself. With this definition, we must write
itself. With this definition, we must write  instead of
instead of  (although it is still also equal to
(although it is still also equal to 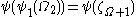 , of course, but it is now constant until
, of course, but it is now constant until 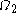 ). This change is inessential because, intuitively speaking, the
). This change is inessential because, intuitively speaking, the 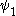 function collapses the nameable ordinals beyond
function collapses the nameable ordinals beyond 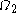 below the latter so it matters little whether
below the latter so it matters little whether 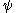 is invoked directly on the ordinals beyond
is invoked directly on the ordinals beyond 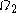 or on their image by
or on their image by 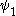 . But it makes it possible to define
. But it makes it possible to define 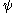 and
and 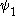 by simultaneous (rather than “downward”) induction, and this is important if we are to use infinitely many collapsing functions.
by simultaneous (rather than “downward”) induction, and this is important if we are to use infinitely many collapsing functions.
Indeed, there is no reason to stop at two levels: using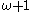 new cardinals in this way,
new cardinals in this way, 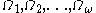 , we get a system essentially equivalent to that introduced by Buchholz, the inessential difference being that since Buchholz uses
, we get a system essentially equivalent to that introduced by Buchholz, the inessential difference being that since Buchholz uses  ordinals from the start, he does not need to allow multiplication or exponentiation; also, Buchholz does not introduce the numbers
ordinals from the start, he does not need to allow multiplication or exponentiation; also, Buchholz does not introduce the numbers 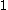 or
or 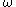 in the system as they will also be produced by the
in the system as they will also be produced by the 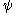 functions: this makes the entire scheme much more elegant and more concise to define, albeit more difficult to understand. This system is also sensibly equivalent to the earlier (and much more difficult to grasp) “ordinal diagrams” of Takeuti and
functions: this makes the entire scheme much more elegant and more concise to define, albeit more difficult to understand. This system is also sensibly equivalent to the earlier (and much more difficult to grasp) “ordinal diagrams” of Takeuti and 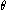 functions of Feferman: their range is the same (
functions of Feferman: their range is the same (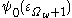 , which could be called the Takeuti-Feferman-Buchholz ordinal, and which describes the strength
, which could be called the Takeuti-Feferman-Buchholz ordinal, and which describes the strength
of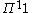 -comprehension).
-comprehension).
, so the collapse of this or that large cardinal must be mentioned simultaneously with the theory for which it provides a proof-theoretic analysis.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an ordinal collapsing function (or projection function) is a technique for defining (notations
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
for) certain recursive
Recursive ordinal
In mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
large countable ordinal
Large countable ordinal
In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal...
s, whose principle is to give names to certain ordinals much larger than the one being defined, perhaps even large cardinals
Large cardinal property
In the mathematical field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the name suggests, generally very "large"...
(though they can be replaced with recursively large ordinals at the cost of extra technical difficulty), and then “collapse” them down to a system of notations for the sought-after ordinal. For this reason, ordinal collapsing functions are described as an impredicative manner of naming ordinals.
The details of the definition of ordinal collapsing functions vary, and get more complicated as greater ordinals are being defined, but the typical idea is that whenever the notation system “runs out of fuel” and cannot name a certain ordinal, a much larger ordinal is brought “from above” to give a name to that critical point. An example of how this works will be detailed below, for an ordinal collapsing function defining the Bachmann-Howard ordinal (i.e., defining a system of notations up to the Bachmann-Howard ordinal).
The use and definition of ordinal collapsing functions is inextricably intertwined with the theory of ordinal analysis
Ordinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
, since the large countable ordinals defined and denoted by a given collapse are used to describe the ordinal-theoretic strength of certain formal systems, typically subsystems of analysis
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
(such as those seen in the light of reverse mathematics
Reverse mathematics
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...
), extensions of Kripke-Platek set theory, Bishop
Errett Bishop
Errett Albert Bishop was an American mathematician known for his work on analysis. He is the father of constructive analysis, because of his 1967 Foundations of Constructive Analysis, where he proved most of the important theorems in real analysis by constructive methods.-Life:Errett Bishop's...
-style systems of constructive mathematics
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
or Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
-style systems of intuitionistic type theory
Intuitionistic type theory
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...
.
Ordinal collapsing functions are typically denoted using some variation of the Greek letter
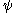 (psi
(psiPsi (letter)
Psi is the 23rd letter of the Greek alphabet and has a numeric value of 700. In both Classical and Modern Greek, the letter indicates the combination /ps/ . The letter was adopted into the Old Italic alphabet, and its shape is continued into the Algiz rune of the Elder Futhark...
).
An example leading up to the Bachmann-Howard ordinal
The choice of the ordinal collapsing function given as example below imitates greatly the system introduced by Buchholz but is limited to collapsing one cardinal for clarity of exposition. More on the relation between this example and Buchholz's system will be said below.Definition
Let stand for the first uncountable ordinal
stand for the first uncountable ordinalFirst uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
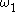 , or, in fact, any ordinal which is (an
, or, in fact, any ordinal which is (an  -number and) guaranteed to be greater than all the countable ordinals which will be constructed (for example, the Church-Kleene ordinal is adequate for our purposes; but we will work with
-number and) guaranteed to be greater than all the countable ordinals which will be constructed (for example, the Church-Kleene ordinal is adequate for our purposes; but we will work with  because it allows the convenient use of the word countable in the definitions).
because it allows the convenient use of the word countable in the definitions).We define a function
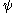 (which will be non-decreasing
(which will be non-decreasingMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
and continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
), taking an arbitrary ordinal
 to a countable ordinal
to a countable ordinal 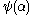 , recursively on
, recursively on  , as follows:
, as follows:- Assume
 has been defined for all
has been defined for all 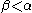 , and we wish to define
, and we wish to define 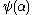 .
.
- Let
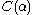 be the set of ordinals generated starting from
be the set of ordinals generated starting from  ,
, 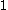 ,
, 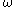 and
and 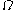 by recursively applying the following functions: ordinal addition, multiplication and exponentiationOrdinal arithmeticIn the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
by recursively applying the following functions: ordinal addition, multiplication and exponentiationOrdinal arithmeticIn the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
and the function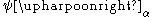 , i.e., the restriction of
, i.e., the restriction of  to ordinals
to ordinals 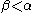 . (Formally, we define
. (Formally, we define 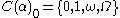 and inductively
and inductively 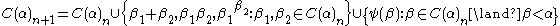 for all natural numbers
for all natural numbers  and we let
and we let 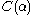 be the union of the
be the union of the 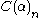 for all
for all  .)
.)
- Then
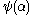 is defined as the smallest ordinal not belonging to
is defined as the smallest ordinal not belonging to 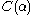 .
.
In a more concise (although more obscure) way:
 is the smallest ordinal which cannot be expressed from
is the smallest ordinal which cannot be expressed from 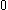 ,
, 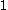 ,
, 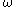 and
and  using sums, products, exponentials, and the
using sums, products, exponentials, and the 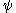 function itself (to previously constructed ordinals less than
function itself (to previously constructed ordinals less than  ).
).Here is an attempt to explain the motivation for the definition of
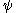 in intuitive terms: since the usual operations of addition, multiplication and exponentiation are not sufficient to designate ordinals very far, we attempt to systematically create new names for ordinals by taking the first one which does not have a name yet, and whenever we run out of names, rather than invent them in an ad hoc fashion or using diagonal schemes, we seek them in the ordinals far beyond the ones we are constructing (beyond
in intuitive terms: since the usual operations of addition, multiplication and exponentiation are not sufficient to designate ordinals very far, we attempt to systematically create new names for ordinals by taking the first one which does not have a name yet, and whenever we run out of names, rather than invent them in an ad hoc fashion or using diagonal schemes, we seek them in the ordinals far beyond the ones we are constructing (beyond 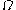 , that is); so we give names to uncountable ordinals and, since in the end the list of names is necessarily countable,
, that is); so we give names to uncountable ordinals and, since in the end the list of names is necessarily countable, 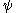 will “collapse” them to countable ordinals.
will “collapse” them to countable ordinals. Computation of values of 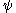
To clarify how the function 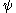 is able to produce notations for certain ordinals, we now compute its first values.
is able to produce notations for certain ordinals, we now compute its first values.Predicative start
First consider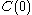 . It contains ordinals
. It contains ordinals 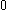 ,
, 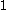 ,
, 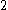 ,
, 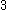 ,
,  ,
,  ,
, 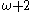 ,
, 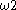 ,
, 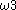 ,
, 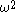 ,
, 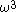 ,
, 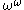 ,
,  and so on. It also contains such ordinals as
and so on. It also contains such ordinals as  ,
,  ,
, 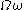 ,
, 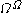 . The first ordinal which it does not contain is
. The first ordinal which it does not contain is 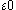
Epsilon nought
In mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like...
(which is the limit of
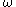 ,
,  ,
, 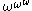 and so on — less than
and so on — less than  by assumption). The upper bound of the ordinals it contains is
by assumption). The upper bound of the ordinals it contains is  (the limit of
(the limit of 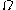 ,
,  ,
, 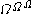 and so on), but that is not so important. This shows that
and so on), but that is not so important. This shows that 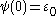 .
.Similarly,
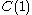 contains the ordinals which can be formed from
contains the ordinals which can be formed from 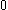 ,
, 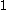 ,
, 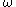 ,
, 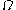 and this time also
and this time also  , using addition, multiplication and exponentiation. This contains all the ordinals up to
, using addition, multiplication and exponentiation. This contains all the ordinals up to 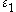 but not the latter, so
but not the latter, so 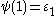 . In this manner, we prove that
. In this manner, we prove that 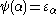 inductively on
inductively on  : the proof works, however, only as long as
: the proof works, however, only as long as 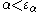 . We therefore have:
. We therefore have: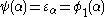 for all
for all 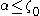 , where
, where 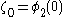 is the smallest fixed point of
is the smallest fixed point of  .
.(Here, the
 functions are the Veblen function
functions are the Veblen functionVeblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
s defined starting with
 .)
.)Now
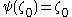 but
but 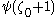 is no larger, since
is no larger, since 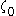 cannot be constructed using finite applications of
cannot be constructed using finite applications of 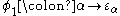 and thus never belongs to a
and thus never belongs to a 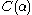 set for
set for 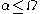 , and the function
, and the function  remains “stuck” at
remains “stuck” at 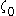 for some time:
for some time: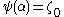 for all
for all 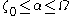 .
.First impredicative values
Again,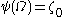 . However, when we come to computing
. However, when we come to computing  , something has changed: since
, something has changed: since 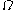 was (“artificially”) added to all the
was (“artificially”) added to all the  , we are permitted to take the value
, we are permitted to take the value 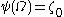 in the process. So
in the process. So 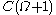 contains all ordinals which can be built from
contains all ordinals which can be built from 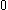 ,
, 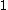 ,
,  ,
, 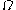 , the
, the 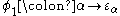 function up to
function up to 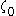 and this time also
and this time also 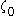 itself, using addition, multiplication and exponentiation. The smallest ordinal not in
itself, using addition, multiplication and exponentiation. The smallest ordinal not in 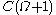 is
is  (the smallest
(the smallest  -number after
-number after 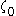 ).
).We say that the definition
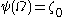 and the next values of the function
and the next values of the function 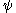 such as
such as 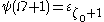 are impredicative because they use ordinals (here,
are impredicative because they use ordinals (here, 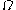 ) greater than the ones which are being defined (here,
) greater than the ones which are being defined (here, 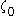 ).
). Values of 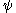 up to the Feferman-Schütte ordinal
up to the Feferman-Schütte ordinal
The fact that 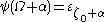 remains true for all
remains true for all 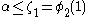 (note, in particular, that
(note, in particular, that 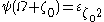 : but since now the ordinal
: but since now the ordinal 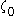 has been constructed there is nothing to prevent from going beyond this). However, at
has been constructed there is nothing to prevent from going beyond this). However, at 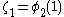 (the first fixed point of
(the first fixed point of 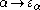 beyond
beyond 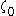 ), the construction stops again, because
), the construction stops again, because  cannot be constructed from smaller ordinals and
cannot be constructed from smaller ordinals and 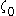 by finitely applying the
by finitely applying the  function. So we have
function. So we have 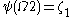 .
.The same reasoning shows that
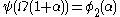 for all
for all 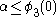 , where
, where  enumerates the fixed points of
enumerates the fixed points of 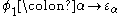 and
and 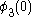 is the first fixed point of
is the first fixed point of  . We then have
. We then have 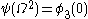 .
.Again, we can see that
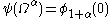 for some time: this remains true until the first fixed point
for some time: this remains true until the first fixed point 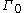 of
of 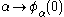 , which is the Feferman-Schütte ordinal. Thus,
, which is the Feferman-Schütte ordinal. Thus, 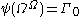 is the Feferman-Schütte ordinal.
is the Feferman-Schütte ordinal.Beyond the Feferman-Schütte ordinal
We have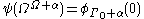 for all
for all 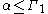 where
where 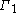 is the next fixed point of
is the next fixed point of 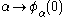 . So, if
. So, if 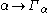 enumerates the fixed points in question. (which can also be noted
enumerates the fixed points in question. (which can also be noted 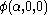 using the many-valued Veblen functions) we have
using the many-valued Veblen functions) we have 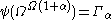 , until the first fixed point of the
, until the first fixed point of the 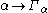 itself, which will be
itself, which will be 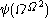 . In this manner:
. In this manner:
-
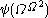 is the Ackermann ordinalAckermann ordinalIn mathematics, the Ackermann ordinal is a certain large countable ordinal, named after Wilhelm Ackermann. The term "Ackermann ordinal" is also occasionally used for the small Veblen ordinal, a somewhat larger ordinal....
is the Ackermann ordinalAckermann ordinalIn mathematics, the Ackermann ordinal is a certain large countable ordinal, named after Wilhelm Ackermann. The term "Ackermann ordinal" is also occasionally used for the small Veblen ordinal, a somewhat larger ordinal....
(the range of the notation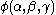 defined predicatively),
defined predicatively), -
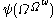 is the “small” Veblen ordinalSmall Veblen ordinalIn mathematics, the small Veblen ordinal is a certain large countable ordinal, named after Oswald Veblen. It is occasionally called the Ackermann ordinal, though the Ackermann ordinal described by is somewhat smaller than the small Veblen ordinal....
is the “small” Veblen ordinalSmall Veblen ordinalIn mathematics, the small Veblen ordinal is a certain large countable ordinal, named after Oswald Veblen. It is occasionally called the Ackermann ordinal, though the Ackermann ordinal described by is somewhat smaller than the small Veblen ordinal....
(the range of the notations predicatively using finitely many variables),
predicatively using finitely many variables), -
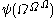 is the “large” Veblen ordinalLarge Veblen ordinalIn mathematics, the large Veblen ordinal is a certain large countable ordinal, named after Oswald Veblen.There is no standard notation for ordinals beyond the Feferman–Schütte ordinal Γ0...
is the “large” Veblen ordinalLarge Veblen ordinalIn mathematics, the large Veblen ordinal is a certain large countable ordinal, named after Oswald Veblen.There is no standard notation for ordinals beyond the Feferman–Schütte ordinal Γ0...
(the range of the notations predicatively using transfinitely-but-predicatively-many variables),
predicatively using transfinitely-but-predicatively-many variables), - the limit
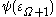 of
of 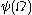 ,
, 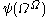 ,
, 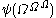 , etc., is the Bachmann-Howard ordinal: after this our function
, etc., is the Bachmann-Howard ordinal: after this our function 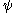 is constant, and we can go no further with the definition we have given.
is constant, and we can go no further with the definition we have given.
Ordinal notations up to the Bachmann-Howard ordinal
We now explain more systematically how the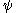 function defines notations for ordinals up to the Bachmann-Howard ordinal.
function defines notations for ordinals up to the Bachmann-Howard ordinal.A note about base representations
Recall that if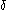 is an ordinal which is a power of
is an ordinal which is a power of 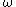 (for example
(for example 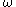 itself, or
itself, or 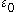 , or
, or 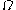 ), any ordinal
), any ordinal  can be uniquely expressed in the form
can be uniquely expressed in the form 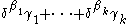 , where
, where 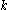 is a natural number,
is a natural number, 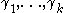 are non-zero ordinals less than
are non-zero ordinals less than 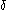 , and
, and 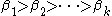 are ordinal numbers (we allow
are ordinal numbers (we allow 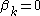 ). This “base
). This “base 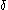 representation” is an obvious generalization of the Cantor normal form (which is the case
representation” is an obvious generalization of the Cantor normal form (which is the case 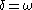 ). Of course, it may quite well be that the expression is uninteresting, i.e.,
). Of course, it may quite well be that the expression is uninteresting, i.e., 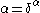 , but in any other case the
, but in any other case the 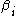 must all be less than
must all be less than  ; it may also be the case that the expression is trivial (i.e.,
; it may also be the case that the expression is trivial (i.e., 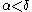 , in which case
, in which case 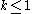 and
and 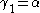 ).
).If
 is an ordinal less than
is an ordinal less than 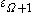 , then its base
, then its base 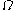 representation has coefficients
representation has coefficients 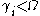 (by definition) and exponents
(by definition) and exponents  (because of the assumption
(because of the assumption 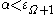 ): hence one can rewrite these exponents in base
): hence one can rewrite these exponents in base 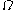 and repeat the operation until the process terminates (any decreasing sequence of ordinals is finite). We call the resulting expression the iterated base
and repeat the operation until the process terminates (any decreasing sequence of ordinals is finite). We call the resulting expression the iterated base 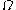 representation of
representation of  and the various coefficients involved (including as exponents) the pieces of the representation (they are all
and the various coefficients involved (including as exponents) the pieces of the representation (they are all 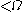 ), or, for short, the
), or, for short, the  -pieces of
-pieces of  .
. Some properties of 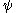
- The function
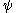 is non-decreasing and continuous (this is more or less obvious from its definition).
is non-decreasing and continuous (this is more or less obvious from its definition). - If
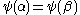 with
with  then necessarily
then necessarily 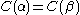 . Indeed, no ordinal
. Indeed, no ordinal 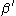 with
with  can belong to
can belong to 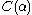 (otherwise its image by
(otherwise its image by 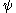 , which is
, which is 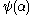 would belong to
would belong to 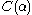 — impossible); so
— impossible); so 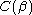 is closed by everything under which
is closed by everything under which 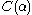 is the closure, so they are equal.
is the closure, so they are equal. - Any value
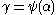 taken by
taken by  is an
is an  -number (i.e., a fixed point of
-number (i.e., a fixed point of 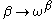 ). Indeed, if it were not, then by writing it in Cantor normal form, it could be expressed using sums, products and exponentiation from elements less than it, hence in
). Indeed, if it were not, then by writing it in Cantor normal form, it could be expressed using sums, products and exponentiation from elements less than it, hence in 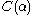 , so it would be in
, so it would be in 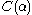 , a contradiction.
, a contradiction. - Lemma: Assume
 is an
is an  -number and
-number and  an ordinal such that
an ordinal such that 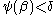 for all
for all  : then the
: then the 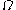 -pieces (defined above) of any element of
-pieces (defined above) of any element of 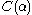 are less than
are less than 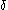 . Indeed, let
. Indeed, let 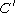 be the set of ordinals all of whose
be the set of ordinals all of whose 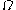 -pieces are less than
-pieces are less than 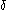 . Then
. Then 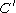 is closed under addition, multiplication and exponentiation (because
is closed under addition, multiplication and exponentiation (because  is an
is an  -number, so ordinals less than it are closed under addition, multiplication and exponentition). And
-number, so ordinals less than it are closed under addition, multiplication and exponentition). And 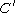 also contains every
also contains every  for
for 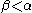 by assumption, and it contains
by assumption, and it contains 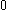 ,
,  ,
, 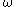 ,
, 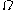 . So
. So  , which was to be shown.
, which was to be shown. - Under the hypothesis of the previous lemma,
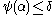 (indeed, the lemma shows that
(indeed, the lemma shows that 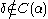 ).
). - Any
 -number less than some element in the range of
-number less than some element in the range of 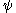 is itself in the range of
is itself in the range of 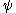 (that is,
(that is, 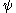 omits no
omits no  -number). Indeed: if
-number). Indeed: if 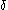 is an
is an  -number not greater than the range of
-number not greater than the range of  , let
, let  be the least upper bound of the
be the least upper bound of the 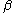 such that
such that 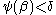 : then by the above we have
: then by the above we have  , but
, but 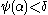 would contradict the fact that
would contradict the fact that  is the least upper bound — so
is the least upper bound — so 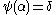 .
. - Whenever
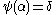 , the set
, the set 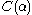 consists exactly of those ordinals
consists exactly of those ordinals 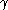 (less than
(less than 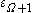 ) all of whose
) all of whose 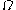 -pieces are less than
-pieces are less than 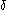 . Indeed, we know that all ordinals less than
. Indeed, we know that all ordinals less than 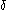 , hence all ordinals (less than
, hence all ordinals (less than 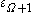 ) whose
) whose 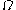 -pieces are less than
-pieces are less than 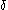 , are in
, are in 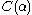 . Conversely, if we assume
. Conversely, if we assume  for all
for all 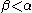 (in other words if
(in other words if  is the least possible with
is the least possible with 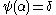 ), the lemma gives the desired property. On the other hand, if
), the lemma gives the desired property. On the other hand, if 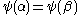 for some
for some 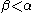 , then we have already remarked
, then we have already remarked 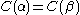 and we can replace
and we can replace  by the least possible with
by the least possible with 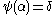 .
.
The ordinal notation
Using the facts above, we can define a (canonical) ordinal notation for every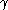 less than the Bachmann-Howard ordinal. We do this by induction on
less than the Bachmann-Howard ordinal. We do this by induction on 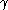 .
.If
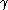 is less than
is less than 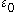 , we use the iterated Cantor normal form of
, we use the iterated Cantor normal form of 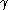 . Otherwise, there exists a largest
. Otherwise, there exists a largest  -number
-number 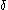 less or equal to
less or equal to  (this is because the set of
(this is because the set of  -numbers is closed): if
-numbers is closed): if  then by induction we have defined a notation for
then by induction we have defined a notation for 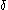 and the base
and the base 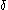 representation of
representation of 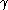 gives one for
gives one for 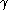 , so we are finished.
, so we are finished.It remains to deal with the case where
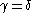 is an
is an  -number: we have argued that, in this case, we can write
-number: we have argued that, in this case, we can write 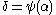 for some (possibly uncountable) ordinal
for some (possibly uncountable) ordinal 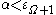 : let
: let  be the greatest possible such ordinal (which exists since
be the greatest possible such ordinal (which exists since 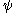 is continuous). We use the iterated base
is continuous). We use the iterated base 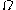 representation of
representation of  : it remains to show that every piece of this representation is less than
: it remains to show that every piece of this representation is less than 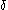 (so we have already defined a notation for it). If this is not the case then, by the properties we have shown,
(so we have already defined a notation for it). If this is not the case then, by the properties we have shown, 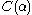 does not contain
does not contain  ; but then
; but then 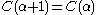 (they are closed under the same operations, since the value of
(they are closed under the same operations, since the value of 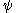 at
at  can never be taken), so
can never be taken), so 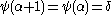 , contradicting the maximality of
, contradicting the maximality of  .
.Note: Actually, we have defined canonical notations not just for ordinals below the Bachmann-Howard ordinal but also for certain uncountable ordinals, namely those whose
 -pieces are less than the Bachmann-Howard ordinal (viz.: write them in iterated base
-pieces are less than the Bachmann-Howard ordinal (viz.: write them in iterated base  representation and use the canonical representation for every piece). This canonical notation is used for arguments of the
representation and use the canonical representation for every piece). This canonical notation is used for arguments of the 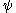 function (which may be uncountable).
function (which may be uncountable).Examples
For ordinals less than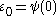 , the canonical ordinal notation defined coincides with the iterated Cantor normal form (by definition).
, the canonical ordinal notation defined coincides with the iterated Cantor normal form (by definition).For ordinals less than
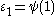 , the notation coincides with iterated base
, the notation coincides with iterated base 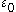 notation (the pieces being themselves written in iterated Cantor normal form): e.g.,
notation (the pieces being themselves written in iterated Cantor normal form): e.g., 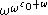 will be written
will be written  , or, more accurately,
, or, more accurately, 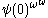 . For ordinals less than
. For ordinals less than 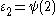 , we similarly write in iterated base
, we similarly write in iterated base 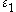 and then write the pieces in iterated base
and then write the pieces in iterated base 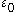 (and write the pieces of that in iterated Cantor normal form): so
(and write the pieces of that in iterated Cantor normal form): so 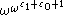 is written
is written 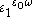 , or, more accurately,
, or, more accurately, 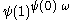 . Thus, up to
. Thus, up to  , we always use the largest possible
, we always use the largest possible  -number base which gives a non-trivial representation.
-number base which gives a non-trivial representation.Beyond this, we may need to express ordinals beyond
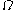 : this is always done in iterated
: this is always done in iterated 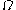 -base, and the pieces themselves need to be expressed using the largest possible
-base, and the pieces themselves need to be expressed using the largest possible  -number base which gives a non-trivial representation.
-number base which gives a non-trivial representation.Note that while
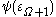 is equal to the Bachmann-Howard ordinal, this is not a “canonical notation” in the sense we have defined (canonical notations are defined only for ordinals less than the Bachmann-Howard ordinal).
is equal to the Bachmann-Howard ordinal, this is not a “canonical notation” in the sense we have defined (canonical notations are defined only for ordinals less than the Bachmann-Howard ordinal).Conditions for canonicalness
The notations thus defined have the property that whenever they nest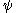 functions, the arguments of the “inner”
functions, the arguments of the “inner” 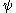 function are always less than those of the “outer” one (this is a consequence of the fact that the
function are always less than those of the “outer” one (this is a consequence of the fact that the 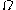 -pieces of
-pieces of  , where
, where  is the largest possible such that
is the largest possible such that 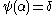 for some
for some  -number
-number 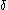 , are all less than
, are all less than 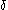 , as we have shown above). For example,
, as we have shown above). For example, 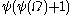 does not occur as a notation: it is a well-defined expression (and it is equal to
does not occur as a notation: it is a well-defined expression (and it is equal to  since
since 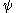 is constant between
is constant between 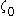 and
and  ), but it is not a notation produced by the inductive algorithm we have outlined.
), but it is not a notation produced by the inductive algorithm we have outlined.Canonicalness can be checked recursively: an expression is canonical if and only if it is either the iterated Cantor normal form of an ordinal less than
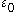 , or an iterated base
, or an iterated base 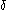 representation all of whose pieces are canonical, for some
representation all of whose pieces are canonical, for some  where
where  is itself written in iterated base
is itself written in iterated base 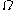 representation all of whose pieces are canonical and less than
representation all of whose pieces are canonical and less than 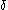 . The order is checked by lexicographic verification at all levels (keeping in mind that
. The order is checked by lexicographic verification at all levels (keeping in mind that 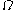 is greater than any expression obtained by
is greater than any expression obtained by 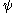 , and for canonical values the greater
, and for canonical values the greater 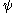 always trumps the lesser or even arbitrary sums, products and exponentials of the lesser).
always trumps the lesser or even arbitrary sums, products and exponentials of the lesser).For example,
 is a canonical notation for an ordinal which is less than the Feferman-Schütte ordinal: it can be written using the Veblen functions as
is a canonical notation for an ordinal which is less than the Feferman-Schütte ordinal: it can be written using the Veblen functions as 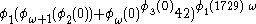 .
.Concerning the order, one might point out that
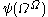 (the Feferman-Schütte ordinal) is much more than
(the Feferman-Schütte ordinal) is much more than 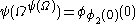 (because
(because 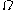 is greater than
is greater than  of anything), and
of anything), and 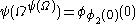 is itself much more than
is itself much more than 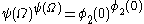 (because
(because 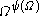 is greater than
is greater than 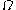 , so any sum-product-or-exponential expression involving
, so any sum-product-or-exponential expression involving 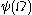 and smaller value will remain less than
and smaller value will remain less than 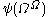 ). In fact,
). In fact,  is already less than
is already less than 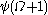 .
.Standard sequences for ordinal notations
To witness the fact that we have defined notations for ordinals below the Bachmann-Howard ordinal (which are all of countable cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
), we might define standard sequences converging to any one of them (provided it is a limit ordinal, of course). Actually we will define canonical sequences for certain uncountable ordinals, too, namely the uncountable ordinals of countable cofinality (if we are to hope to define a sequence converging to them…) which are representable (that is, all of whose
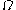 -pieces are less than the Bachmann-Howard ordinal).
-pieces are less than the Bachmann-Howard ordinal).The following rules are more or less obvious, except for the last:
- First, get rid of the (iterated) base
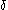 representations: to define a standard sequence converging to
representations: to define a standard sequence converging to 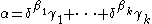 , where
, where 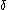 is either
is either 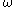 or
or  (or
(or 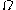 , but see below):
, but see below):
- if
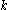 is zero then
is zero then 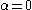 and there is nothing to be done;
and there is nothing to be done; - if
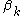 is zero and
is zero and 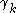 is successor, then
is successor, then  is successor and there is nothing to be done;
is successor and there is nothing to be done; - if
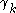 is limit, take the standard sequence converging to
is limit, take the standard sequence converging to 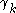 and replace
and replace 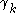 in the expression by the elements of that sequence;
in the expression by the elements of that sequence; - if
 is successor and
is successor and  is limit, rewrite the last term
is limit, rewrite the last term 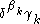 as
as 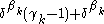 and replace the exponent
and replace the exponent 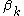 in the last term by the elements of the fundamental sequence converging to it;
in the last term by the elements of the fundamental sequence converging to it; - if
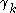 is successor and
is successor and 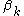 is also, rewrite the last term
is also, rewrite the last term 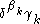 as
as 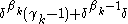 and replace the last
and replace the last 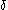 in this expression by the elements of the fundamental sequence converging to it.
in this expression by the elements of the fundamental sequence converging to it.
- if
- If
 is
is 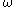 , then take the obvious
, then take the obvious 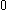 ,
, 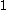 ,
, 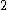 ,
,  … as the fundamental sequence for
… as the fundamental sequence for 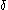 .
. - If
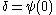 then take as fundamental sequence for
then take as fundamental sequence for 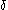 the sequence
the sequence 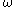 ,
, 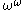 ,
, 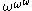 …
… - If
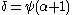 then take as fundamental sequence for
then take as fundamental sequence for 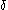 the sequence
the sequence 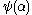 ,
, 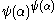 ,
, 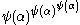 …
… - If
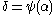 where
where  is a limit ordinal of countable cofinality, define the standard sequence for
is a limit ordinal of countable cofinality, define the standard sequence for 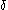 to be obtained by applying
to be obtained by applying 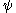 to the standard sequence for
to the standard sequence for  (recall that
(recall that 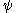 is continuous, here).
is continuous, here). - It remains to handle the case where
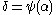 with
with  an ordinal of uncountable cofinality (e.g.,
an ordinal of uncountable cofinality (e.g.,  itself). Obviously it doesn't make sense to define a sequence converging to
itself). Obviously it doesn't make sense to define a sequence converging to  in this case; however, what we can define is a sequence converging to some
in this case; however, what we can define is a sequence converging to some 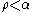 with countable cofinality and such that
with countable cofinality and such that 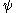 is constant between
is constant between 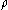 and
and  . This
. This 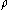 will be the first fixed point of a certain (continuous and non-decreasing) function
will be the first fixed point of a certain (continuous and non-decreasing) function 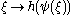 . To find it, apply the same rules (from the base
. To find it, apply the same rules (from the base 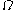 representation of
representation of  ) as to find the canonical sequence of
) as to find the canonical sequence of  , except that whenever a sequence converging to
, except that whenever a sequence converging to 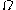 is called for (something which cannot exist), replace the
is called for (something which cannot exist), replace the 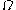 in question, in the expression of
in question, in the expression of 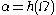 , by a
, by a 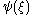 (where
(where 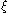 is a variable) and perform a repeated iteration (starting from
is a variable) and perform a repeated iteration (starting from 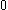 , say) of the function
, say) of the function 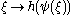 : this gives a sequence
: this gives a sequence  ,
, 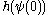 ,
, 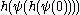 … tending to
… tending to  , and the canonical sequence for
, and the canonical sequence for 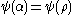 is
is 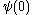 ,
,  ,
, 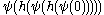 … (The examples below should make this clearer.)
… (The examples below should make this clearer.)
Here are some examples for the last (and most interesting) case:
- The canonical sequence for
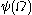 is:
is: 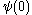 ,
, 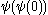 ,
, 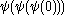 … This indeed converges to
… This indeed converges to 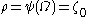 after which
after which 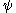 is constant until
is constant until 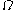 .
. - The canonical sequence for
 is:
is:  ,
, 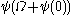 ,
, 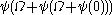 … This indeed converges to the value of
… This indeed converges to the value of  at
at 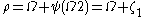 after which
after which  is constant until
is constant until 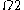 .
. - The canonical sequence for
 is:
is: 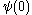 ,
, 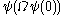 ,
,  … This converges to the value of
… This converges to the value of 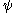 at
at 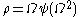 .
. - The canonical sequence for
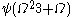 is
is  ,
, 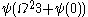 ,
, 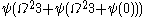 … This converges to the value of
… This converges to the value of 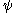 at
at 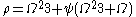 .
. - The canonical sequence for
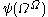 is:
is: 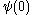 ,
, 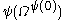 ,
,  … This converges to the value of
… This converges to the value of  at
at 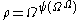 .
. - The canonical sequence for
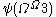 is:
is: 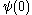 ,
, 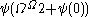 ,
, 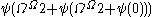 … This converges to the value of
… This converges to the value of 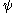 at
at  .
. - The canonical sequence for
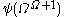 is:
is: 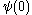 ,
, 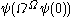 ,
, 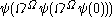 … This converges to the value of
… This converges to the value of 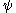 at
at 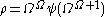 .
. - The canonical sequence for
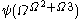 is:
is: 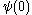 ,
, 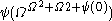 ,
, 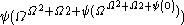 …
…
Here are some examples of the other cases:
- The canonical sequence for
 is:
is: 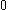 ,
, 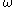 ,
, 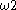 ,
, 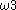 …
… - The canonical sequence for
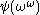 is:
is:  ,
, 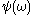 ,
,  ,
, 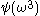 …
… - The canonical sequence for
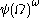 is:
is: 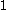 ,
, 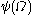 ,
, 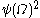 ,
, 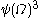 …
… - The canonical sequence for
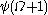 is:
is: 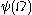 ,
, 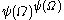 ,
,  …
… - The canonical sequence for
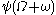 is:
is: 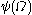 ,
, 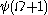 ,
,  ,
, 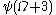 …
… - The canonical sequence for
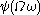 is:
is: 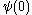 ,
,  ,
,  ,
, 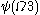 …
… - The canonical sequence for
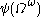 is:
is: 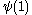 ,
,  ,
, 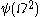 ,
, 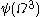 …
… - The canonical sequence for
 is:
is: 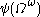 ,
, 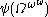 ,
, 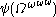 … (this is derived from the fundamental sequence for
… (this is derived from the fundamental sequence for 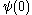 ).
). - The canonical sequence for
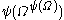 is:
is: 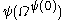 ,
, 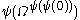 ,
, 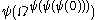 … (this is derived from the fundamental sequence for
… (this is derived from the fundamental sequence for 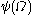 , which was given above).
, which was given above).
Even though the Bachmann-Howard ordinal
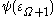 itself has no canonical notation, it is also useful to define a canonical sequence for it: this is
itself has no canonical notation, it is also useful to define a canonical sequence for it: this is 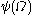 ,
, 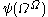 ,
, 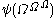 …
…A terminating process
Start with any ordinal less or equal to the Bachmann-Howard ordinal, and repeat the following process so long as it is not zero:- if the ordinal is a successor, subtract one (that is, replace it with its predecessor),
- if it is a limit, replace it by some element of the canonical sequence defined for it.
Then it is true that this process always terminates (as any decreasing sequence of ordinals is finite); however, like (but even more so than for) the hydra game
Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, made by Reuben Goodstein, which states that every Goodstein sequence eventually terminates at 0. showed that it is unprovable in Peano arithmetic...
:
- it can take a very long time to terminate,
- the proof of termination may be out of reach of certain weak systems of arithmetic.
To give some flavor of what the process feels like, here are some steps of it: starting from
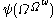 (the small Veblen ordinal), we might go down to
(the small Veblen ordinal), we might go down to 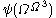 , from there down to
, from there down to 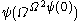 , then
, then  then
then 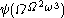 then
then 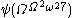 then
then 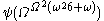 then
then  then
then 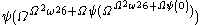 and so on. It appears as though the expressions are getting more and more complicated whereas, in fact, the ordinals always decrease.
and so on. It appears as though the expressions are getting more and more complicated whereas, in fact, the ordinals always decrease.Concerning the first statement, one could introduce, for any ordinal
 less or equal to the Bachmann-Howard ordinal
less or equal to the Bachmann-Howard ordinal 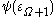 , the integer function
, the integer function 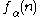 which counts the number of steps of the process before termination if one always selects the
which counts the number of steps of the process before termination if one always selects the  'th element from the canonical sequence. Then
'th element from the canonical sequence. Then 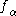 can be a very fast growing function: already
can be a very fast growing function: already 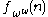 is essentially
is essentially  , the function
, the function 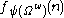 is comparable with the Ackermann function
is comparable with the Ackermann functionAckermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
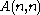 , and
, and 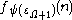 is quite unimaginable.
is quite unimaginable.Concerning the second statement, a precise version is given by ordinal analysis
Ordinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
: for example, Kripke-Platek set theory can prove that the process terminates for any given
 less than the Bachmann-Howard ordinal, but it cannot do this uniformly, i.e., it cannot prove the termination starting from the Bachmann-Howard ordinal. Some theories like Peano arithmetic are limited by much smaller ordinals (
less than the Bachmann-Howard ordinal, but it cannot do this uniformly, i.e., it cannot prove the termination starting from the Bachmann-Howard ordinal. Some theories like Peano arithmetic are limited by much smaller ordinals (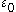 in the case of Peano arithmetic).
in the case of Peano arithmetic).Making the function less powerful
It is instructive (although not exactly useful) to make less powerful.
less powerful.If we alter the definition of
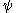 above to omit exponentiation from the repertoire from which
above to omit exponentiation from the repertoire from which 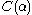 is constructed, then we get
is constructed, then we get 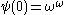 (as this is the smallest ordinal which cannot be constructed from
(as this is the smallest ordinal which cannot be constructed from  ,
,  and
and 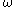 using addition and multiplication only), then
using addition and multiplication only), then 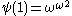 and similarly
and similarly 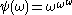 ,
,  until we come to a fixed point which is then our
until we come to a fixed point which is then our 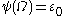 . We then have
. We then have 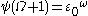 and so on until
and so on until 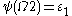 . Since multiplication of
. Since multiplication of 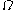 's is permitted, we can still form
's is permitted, we can still form 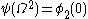 and
and 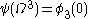 and so on, but our construction ends there as there is no way to get at or beyond
and so on, but our construction ends there as there is no way to get at or beyond 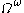 : so the range of this weakened system of notation is
: so the range of this weakened system of notation is 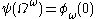 (the value of
(the value of  is the same in our weaker system as in our original system, except that now we cannot go beyond it). This does not even go as far as the Feferman-Schütte ordinal.
is the same in our weaker system as in our original system, except that now we cannot go beyond it). This does not even go as far as the Feferman-Schütte ordinal.If we alter the definition of
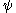 yet some more to allow only addition as a primitive for construction, we get
yet some more to allow only addition as a primitive for construction, we get 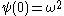 and
and 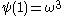 and so on until
and so on until 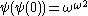 and still
and still  . This time,
. This time, 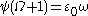 and so on until
and so on until  and similarly
and similarly  . But this time we can go no further: since we can only add
. But this time we can go no further: since we can only add 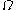 's, the range of our system is
's, the range of our system is 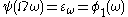 .
.In both cases, we find that the limitation on the weakened
 function comes not so much from the operations allowed on the countable ordinals as on the uncountable ordinals we allow ourselves to denote.
function comes not so much from the operations allowed on the countable ordinals as on the uncountable ordinals we allow ourselves to denote.Going beyond the Bachmann-Howard ordinal
We know that is the Bachmann-Howard ordinal. The reason why
is the Bachmann-Howard ordinal. The reason why 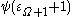 is no larger, with our definitions, is that there is no notation for
is no larger, with our definitions, is that there is no notation for 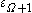 (it does not belong to
(it does not belong to 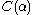 for any
for any  , it is always the least upper bound of it). One could try to add the
, it is always the least upper bound of it). One could try to add the  function (or the Veblen functions of so-many-variables) to the allowed primitives beyond addition, multiplication and exponentiation, but that does not get us very far. To create more systematic notations for countable ordinals, we need more systematic notations for uncountable ordinals: we cannot use the
function (or the Veblen functions of so-many-variables) to the allowed primitives beyond addition, multiplication and exponentiation, but that does not get us very far. To create more systematic notations for countable ordinals, we need more systematic notations for uncountable ordinals: we cannot use the 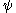 function itself because it only yields countable ordinals (e.g.,
function itself because it only yields countable ordinals (e.g., 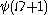 is,
is, 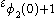 , certainly not
, certainly not  ), so the idea is to mimic its definition as follows:
), so the idea is to mimic its definition as follows:- Let
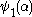 be the smallest ordinal which cannot be expressed from all countable ordinals,
be the smallest ordinal which cannot be expressed from all countable ordinals, 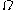 and
and  using sums, products, exponentials, and the
using sums, products, exponentials, and the 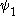 function itself (to previously constructed ordinals less than
function itself (to previously constructed ordinals less than  ).
).
Here,
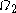 is a new ordinal guaranteed to be greater than all the ordinals which will be constructed using
is a new ordinal guaranteed to be greater than all the ordinals which will be constructed using 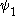 : again, letting
: again, letting 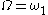 and
and  works.
works.For example,
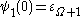 , and more generally
, and more generally 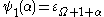 for all countable ordinals and even beyond (
for all countable ordinals and even beyond (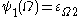 and
and 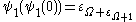 ): this holds up to the first fixed point
): this holds up to the first fixed point 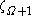 beyond
beyond  of the
of the 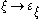 function, which is the limit of
function, which is the limit of 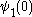 ,
, 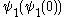 and so forth. Beyond this, we have
and so forth. Beyond this, we have 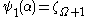 and this remains true until
and this remains true until 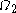 : exactly as was the case for
: exactly as was the case for 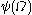 , we have
, we have 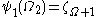 and
and 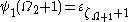 .
.The
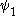 function gives us a system of notations (assuming we can somehow write down all countable ordinals!) for the uncountable ordinals below
function gives us a system of notations (assuming we can somehow write down all countable ordinals!) for the uncountable ordinals below 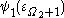 , which is the limit of
, which is the limit of 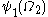 ,
, 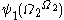 and so forth.
and so forth.Now we can reinject these notations in the original
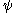 function, modified as follows:
function, modified as follows: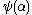 is the smallest ordinal which cannot be expressed from
is the smallest ordinal which cannot be expressed from  ,
,  ,
, 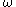 ,
,  and
and  using sums, products, exponentials, the
using sums, products, exponentials, the  function, and the
function, and the 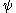 function itself (to previously constructed ordinals less than
function itself (to previously constructed ordinals less than  ).
).This modified function
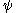 coincides with the previous one up to (and including)
coincides with the previous one up to (and including) 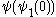 — which is the Bachmann-Howard ordinal. But now we can get beyond this, and
— which is the Bachmann-Howard ordinal. But now we can get beyond this, and 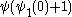 is
is 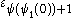 (the next
(the next  -number after the Bachmann-Howard ordinal). We have made our system doubly impredicative: to create notations for countable ordinals we use notations for certain ordinals between
-number after the Bachmann-Howard ordinal). We have made our system doubly impredicative: to create notations for countable ordinals we use notations for certain ordinals between 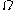 and
and 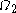 which are themselves defined using certain ordinals beyond
which are themselves defined using certain ordinals beyond 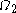 .
.A variation on this scheme, which makes little difference when using just two (or finitely many) collapsing functions, but becomes important for infinitely many of them, is to define
 is the smallest ordinal which cannot be expressed from
is the smallest ordinal which cannot be expressed from  ,
, 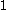 ,
, 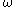 ,
,  and
and  using sums, products, exponentials, and the
using sums, products, exponentials, and the 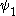 and
and 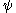 function (to previously constructed ordinals less than
function (to previously constructed ordinals less than  ).
).i.e., allow the use of
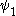 only for arguments less than
only for arguments less than  itself. With this definition, we must write
itself. With this definition, we must write  instead of
instead of  (although it is still also equal to
(although it is still also equal to 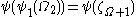 , of course, but it is now constant until
, of course, but it is now constant until 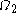 ). This change is inessential because, intuitively speaking, the
). This change is inessential because, intuitively speaking, the 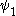 function collapses the nameable ordinals beyond
function collapses the nameable ordinals beyond 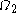 below the latter so it matters little whether
below the latter so it matters little whether 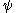 is invoked directly on the ordinals beyond
is invoked directly on the ordinals beyond 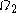 or on their image by
or on their image by 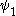 . But it makes it possible to define
. But it makes it possible to define 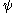 and
and 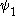 by simultaneous (rather than “downward”) induction, and this is important if we are to use infinitely many collapsing functions.
by simultaneous (rather than “downward”) induction, and this is important if we are to use infinitely many collapsing functions.Indeed, there is no reason to stop at two levels: using
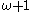 new cardinals in this way,
new cardinals in this way, 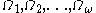 , we get a system essentially equivalent to that introduced by Buchholz, the inessential difference being that since Buchholz uses
, we get a system essentially equivalent to that introduced by Buchholz, the inessential difference being that since Buchholz uses  ordinals from the start, he does not need to allow multiplication or exponentiation; also, Buchholz does not introduce the numbers
ordinals from the start, he does not need to allow multiplication or exponentiation; also, Buchholz does not introduce the numbers 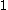 or
or 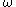 in the system as they will also be produced by the
in the system as they will also be produced by the 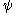 functions: this makes the entire scheme much more elegant and more concise to define, albeit more difficult to understand. This system is also sensibly equivalent to the earlier (and much more difficult to grasp) “ordinal diagrams” of Takeuti and
functions: this makes the entire scheme much more elegant and more concise to define, albeit more difficult to understand. This system is also sensibly equivalent to the earlier (and much more difficult to grasp) “ordinal diagrams” of Takeuti and 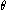 functions of Feferman: their range is the same (
functions of Feferman: their range is the same (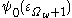 , which could be called the Takeuti-Feferman-Buchholz ordinal, and which describes the strength
, which could be called the Takeuti-Feferman-Buchholz ordinal, and which describes the strengthOrdinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
of
 -comprehension).
-comprehension).Collapsing large cardinals
As noted in the introduction, the use and definition of ordinal collapsing functions is strongly connected with the theory of ordinal analysisOrdinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
, so the collapse of this or that large cardinal must be mentioned simultaneously with the theory for which it provides a proof-theoretic analysis.
- Gerhard Jäger and Wolfram Pohlers described the collapse of an inaccessible cardinalInaccessible cardinalIn set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
to describe the ordinal-theoretic strength of Kripke-Platek set theory augmented by the recursive inaccessibility of the class of ordinals (KPi), which is also proof-theoretically equivalent to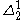 -comprehension plus bar inductionBar inductionBar induction is a reasoning principle used in intuitionistic mathematics, introduced by L.E.J. Brouwer.It is useful in giving constructive versions of classical results.It is based on an inductive argument....
-comprehension plus bar inductionBar inductionBar induction is a reasoning principle used in intuitionistic mathematics, introduced by L.E.J. Brouwer.It is useful in giving constructive versions of classical results.It is based on an inductive argument....
. Roughly speaking, this collapse can be obtained by adding the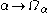 function itself to the list of constructions to which the
function itself to the list of constructions to which the 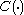 collapsing system applies.
collapsing system applies. - Michael Rathjen then described the collapse of a Mahlo cardinalMahlo cardinalIn mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
to describe the ordinal-theoretic strength of Kripke-Platek set theory augmented by the recursive mahloness of the class of ordinals (KPM). - The same author later described the collapse of a weakly compact cardinalWeakly compact cardinalIn mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
to describe the ordinal-theoretic strength of Kripke-Platek set theory augmented by certain reflection principleReflection principleIn set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...
s (concentrating on the case of -reflection). Very roughly speaking, this proceeds by introducing the first cardinal
-reflection). Very roughly speaking, this proceeds by introducing the first cardinal 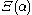 which is
which is  -hyper-Mahlo and adding the
-hyper-Mahlo and adding the 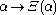 function itself to the collapsing system.
function itself to the collapsing system. - Even more recently, the same author has begun the investigation of the collapse of yet larger cardinals, with the ultimate goal of achieving an ordinal analysis of
 -comprehension (which is proof-theoretically equivalent to the augmentation of Kripke-Platek by
-comprehension (which is proof-theoretically equivalent to the augmentation of Kripke-Platek by  -separation).
-separation).

