
Small Veblen ordinal
Encyclopedia
In mathematics, the small Veblen ordinal is a certain large countable ordinal
, named after Oswald Veblen
. It is occasionally called the Ackermann ordinal, though the Ackermann ordinal
described by is somewhat smaller than the small Veblen ordinal.
Unfortunately there is no standard notation for ordinals beyond the Feferman–Schütte ordinal
Γ0. Most systems of notation use symbols such as ψ(α), θ(α), ψα(β), some of which are modifications of the Veblen function
s to produce countable ordinals even for uncountable arguments, and some of which are "collapsing functions".
The small Veblen ordinal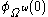 or
or 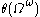 or
or 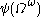 is the limit of ordinals that can be described using a version of Veblen function
is the limit of ordinals that can be described using a version of Veblen function
s with finitely many arguments. It is the ordinal that measures the strength of Kruskal's theorem. It is also the ordinal type of a certain ordering of rooted trees .
Large countable ordinal
In the mathematical discipline of set theory, there are many ways of describing specific countable ordinals. The smallest ones can be usefully and non-circularly expressed in terms of their Cantor normal forms. Beyond that, many ordinals of relevance to proof theory still have computable ordinal...
, named after Oswald Veblen
Oswald Veblen
Oswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...
. It is occasionally called the Ackermann ordinal, though the Ackermann ordinal
Ackermann ordinal
In mathematics, the Ackermann ordinal is a certain large countable ordinal, named after Wilhelm Ackermann. The term "Ackermann ordinal" is also occasionally used for the small Veblen ordinal, a somewhat larger ordinal....
described by is somewhat smaller than the small Veblen ordinal.
Unfortunately there is no standard notation for ordinals beyond the Feferman–Schütte ordinal
Feferman–Schütte ordinal
In mathematics, the Feferman–Schütte ordinal Γ0 is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as arithmetical transfinite recursion.It is named after Solomon Feferman and Kurt Schütte....
Γ0. Most systems of notation use symbols such as ψ(α), θ(α), ψα(β), some of which are modifications of the Veblen function
Veblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
s to produce countable ordinals even for uncountable arguments, and some of which are "collapsing functions".
The small Veblen ordinal
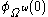 or
or 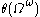 or
or 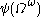 is the limit of ordinals that can be described using a version of Veblen function
is the limit of ordinals that can be described using a version of Veblen functionVeblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
s with finitely many arguments. It is the ordinal that measures the strength of Kruskal's theorem. It is also the ordinal type of a certain ordering of rooted trees .

