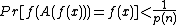One-way function
Encyclopedia
In computer science
, a one-way function is a function
that is easy to compute on every input, but hard to invert given the image
of a random input. Here "easy" and "hard" are to be understood in the sense of computational complexity theory
, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient of a function for it to be called one-way (see Theoretical Definition, below).
The existence of such one-way functions is still an open conjecture. In fact, their existence would prove that the complexity classes P and NP are not equal, thus resolving the foremost unsolved question of theoretical computer science. Existence of a proof that P and NP are not equal would not directly imply the existence of one-way functions.
In applied contexts, the terms "easy" and "hard" are usually interpreted relative to some specific computing entity; typically "cheap enough for the legitimate users" and "prohibitively expensive for any malicious agent
s". One-way functions, in this sense, are fundamental tools for cryptography
, personal identification, authentication
, and other data security
applications. While the existence of such functions too is an open conjecture, there are several candidates that have withstood decades of intense scrutiny. Some of them are essential ingredients of most telecommunication
s, e-commerce, and e-banking
systems around the world.
for every positive polynomial p(n) and sufficiently large n, assuming that x is chosen from the uniform distribution
on {0, 1}n and the randomness of A. In this definition, it is crucial that A may run in time polynomial in |x|.
Note that, by this definition, the function must be "hard to invert" in the average-case, rather than worst-case
sense; while in most of complexity theory (e.g., NP-hard
ness) the term "hard" is meant in the worst-case.
Note also that just making a function "lossy" (not one-to-one) does not make it a one-way function. In this context, inverting a function means identifying some preimage element of a given value, which does not require the existence of an inverse function
. For example, f(x) = x2 is not invertible (for example f(2) = f(-2) = 4) but is also not one-way, since given any value, you can compute one of its preimage elements in polynomial time by taking its square root.
A one-way permutation is a one-way function that is also a permutation—that is, a one-way function that is both injective
and surjective. One-way permutations are an important cryptographic primitive
, and it is not known that their existence is implied by the existence of one-way functions.
A collision-free hash function f is a one-way function that is also collision-resistant; that is, no randomized polynomial time algorithm can find a collision—distinct values x, y such that f(x) = f(y)—with non-negligible probability.
The existence of a one-way function implies the existence of many other useful concepts, including:
these functions are indeed one-way; but extensive research has so far failed to produce an efficient inverting algorithm for any of them.
time where n is the total length (number of digits) of the inputs. Inverting this function requires finding the factors
of a given integer N. The best factoring algorithms known for this problem run in time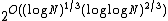
, which is only pseudo-polynomial
in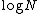
, the number of bits needed to represent N.
This function can be generalized by allowing p and q to range over a suitable set of semiprimes. Note that f is not one-way for arbitrary p,q>1, since the product will have 2 as a factor with probability 3/4.
) The Rabin cryptosystem
is based on the assumption that this Rabin function is one-way.
modulo p; namely, given a prime p and an integer y between 0 and p−1, find x such that 2x = y. As of 2009, there is no published algorithm for this problem that runs in polynomial time. The ElGamal encryption
scheme is based on this function.
s that are fast to compute like SHA 256. Some of the simpler versions have fallen to sophisticated analysis, but the strongest versions continue to offer fast, practical solutions for one-way computation. Most of the theoretical support for the functions are more techniques for thwarting some of the previously successful attacks.
s, the subset sum problem (Naccache-Stern knapsack cryptosystem
), or other problems.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a one-way function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is easy to compute on every input, but hard to invert given the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a random input. Here "easy" and "hard" are to be understood in the sense of computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, specifically the theory of polynomial time problems. Not being one-to-one is not considered sufficient of a function for it to be called one-way (see Theoretical Definition, below).
The existence of such one-way functions is still an open conjecture. In fact, their existence would prove that the complexity classes P and NP are not equal, thus resolving the foremost unsolved question of theoretical computer science. Existence of a proof that P and NP are not equal would not directly imply the existence of one-way functions.
In applied contexts, the terms "easy" and "hard" are usually interpreted relative to some specific computing entity; typically "cheap enough for the legitimate users" and "prohibitively expensive for any malicious agent
Black hat
A black hat is the villain or bad guy, especially in a western movie in which such a character would stereotypically wear a black hat in contrast to the hero's white hat, especially in black and white movies....
s". One-way functions, in this sense, are fundamental tools for cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, personal identification, authentication
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
, and other data security
Data security
Data security is the means of ensuring that data is kept safe from corruption and that access to it is suitably controlled. Thus data security helps to ensure privacy. It also helps in protecting personal data. Data security is part of the larger practice of Information security.- Disk Encryption...
applications. While the existence of such functions too is an open conjecture, there are several candidates that have withstood decades of intense scrutiny. Some of them are essential ingredients of most telecommunication
Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
s, e-commerce, and e-banking
Online banking
Online banking allows customers to conduct financial transactions on a secure website operated by their retail or virtual bank, credit union or building society.-Features:...
systems around the world.
Theoretical definition
A function f: {0, 1}* → {0, 1}* is one-way if f can be computed by a polynomial time algorithm, but for every randomized polynomial time algorithm A,
for every positive polynomial p(n) and sufficiently large n, assuming that x is chosen from the uniform distribution
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
on {0, 1}n and the randomness of A. In this definition, it is crucial that A may run in time polynomial in |x|.
Note that, by this definition, the function must be "hard to invert" in the average-case, rather than worst-case
Best, worst and average case
In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
sense; while in most of complexity theory (e.g., NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
ness) the term "hard" is meant in the worst-case.
Note also that just making a function "lossy" (not one-to-one) does not make it a one-way function. In this context, inverting a function means identifying some preimage element of a given value, which does not require the existence of an inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
. For example, f(x) = x2 is not invertible (for example f(2) = f(-2) = 4) but is also not one-way, since given any value, you can compute one of its preimage elements in polynomial time by taking its square root.
Related concepts
A trapdoor one-way function or trapdoor permutation is a special kind of one-way function. Such a function is hard to invert unless some secret information, called the trapdoor, is known.A one-way permutation is a one-way function that is also a permutation—that is, a one-way function that is both injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and surjective. One-way permutations are an important cryptographic primitive
Cryptographic primitive
Cryptographic primitives are well-established, low-level cryptographic algorithms that are frequently used to build computer security systems. These routines include, but are not limited to, one-way hash functions and encryption functions.- Rationale :...
, and it is not known that their existence is implied by the existence of one-way functions.
A collision-free hash function f is a one-way function that is also collision-resistant; that is, no randomized polynomial time algorithm can find a collision—distinct values x, y such that f(x) = f(y)—with non-negligible probability.
Theoretical implications of one-way functions
If f is a one-way function, then the inversion of f would be a problem whose output is hard to compute (by definition) but easy to check (just by computing f on it). Thus, the existence of a one-way function implies that P≠NP. However, it is not known whether P≠NP implies the existence of one-way functions.The existence of a one-way function implies the existence of many other useful concepts, including:
- Pseudorandom generatorPseudorandom generatorIn theoretical computer science, a pseudorandom generator is a deterministic procedure that produces a pseudorandom distribution from a short uniform input, known as a random seed.-Definition:...
s - Pseudorandom functionPseudorandom functionIn cryptography, a pseudorandom function family, abbreviated PRF, is a collection of efficiently-computable functions which emulate a random oracle in the following way: no efficient algorithm can distinguish between a function chosen randomly from the PRF family and a random oracle...
families - Bit commitment schemesCommitment schemeIn cryptography, a commitment scheme allows one to commit to a value while keeping it hidden, with the ability to reveal the committed value later. Commitments are used to bind a party to a value so that they cannot adapt to other messages in order to gain some kind of inappropriate advantage...
- Private-key encryption schemes secure against adaptive chosen-ciphertext attackAdaptive chosen-ciphertext attackAn adaptive chosen-ciphertext attack is an interactive form of chosen-ciphertext attack in which an attacker sends a number of ciphertexts to be decrypted, then uses the results of these decryptions to select subsequent ciphertexts...
- Message authentication codeMessage authentication codeIn cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...
s - Digital signature schemes (secure against adaptive chosen-message attack)
Candidates for one-way functions
Following are several candidates for one-way functions (as of April 2009). Clearly, it is not known whetherthese functions are indeed one-way; but extensive research has so far failed to produce an efficient inverting algorithm for any of them.
Multiplication and factoring
The function f takes as inputs two prime numbers p and q in binary notation and returns their product. This function can be computed in O(n2)Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
time where n is the total length (number of digits) of the inputs. Inverting this function requires finding the factors
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
of a given integer N. The best factoring algorithms known for this problem run in time
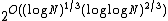, which is only pseudo-polynomialPseudo-polynomial time
In computational complexity theory, a numeric algorithm runs in pseudo-polynomial time if its running time is polynomial in the numeric value of the input ....
in
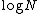, the number of bits needed to represent N.This function can be generalized by allowing p and q to range over a suitable set of semiprimes. Note that f is not one-way for arbitrary p,q>1, since the product will have 2 as a factor with probability 3/4.
Modular squaring and square roots
The function f takes two positive integers x and N, where N is the product of two primes p and q, and outputs the remainder of x2 divided by N. Inverting this function requires computing square roots modulo N; that is, given y and N, find some x such that x2 mod N = y. It can be shown that the latter problem is computationally equivalent to factoring N (in the sense of polynomial-time reductionPolynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
) The Rabin cryptosystem
Rabin cryptosystem
The Rabin cryptosystem is an asymmetric cryptographic technique, whose security, like that of RSA, is related to the difficulty of factorization. However the Rabin cryptosystem has the advantage that the problem on which it relies has been proved to be as hard as integer factorization, which is...
is based on the assumption that this Rabin function is one-way.
Discrete exponential and logarithm
The function f takes a prime number p and an integer x between 0 and p−1; and returns the remainder of 2x divided by p. This discrete exponential function can be easily computed in time O(n3) where n is the number of bits in p. Inverting this function requires computing the discrete logarithmDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
modulo p; namely, given a prime p and an integer y between 0 and p−1, find x such that 2x = y. As of 2009, there is no published algorithm for this problem that runs in polynomial time. The ElGamal encryption
ElGamal encryption
In cryptography, the ElGamal encryption system is an asymmetric key encryption algorithm for public-key cryptography which is based on the Diffie–Hellman key exchange. It was described by Taher Elgamal in 1984. ElGamal encryption is used in the free GNU Privacy Guard software, recent versions of...
scheme is based on this function.
Cryptographically secure hash functions
There are a number of cryptographic hash functionCryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
s that are fast to compute like SHA 256. Some of the simpler versions have fallen to sophisticated analysis, but the strongest versions continue to offer fast, practical solutions for one-way computation. Most of the theoretical support for the functions are more techniques for thwarting some of the previously successful attacks.
Other candidates
Other candidates for one-way functions have been based on the hardness of the decoding of random linear codeLinear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
s, the subset sum problem (Naccache-Stern knapsack cryptosystem
Naccache-Stern knapsack cryptosystem
Note: this is not to be confused with the Naccache–Stern cryptosystem based on the higher residuosity problem.The Naccache–Stern Knapsack Cryptosystem is an atypical public-key cryptosystem developed by David Naccache and Jacques Stern in 1997. This cryptosystem is deterministic, and hence is not...
), or other problems.
Universal one-way function
There is an explicit function which has been demonstrated to be one-way if and only if one-way functions exist. Since this function was the first combinatorial complete one-way function to be demonstrated, it is known as the "universal one-way function". The problem of determining the existence of one-way functions is thus reduced to the problem of proving that this specific function is one-way.Further reading
- Jonathan Katz and Yehuda Lindell (2007). Introduction to Modern Cryptography. CRC Press. ISBN 1-584-88551-3. Section 10.6.3: One-way functions, pp. 374–376. Section 12.1: One-way functions, pp. 279–298.