ElGamal encryption
Encyclopedia
In cryptography
, the ElGamal encryption system is an asymmetric key encryption algorithm for public-key cryptography
which is based on the Diffie–Hellman key exchange. It was described by Taher Elgamal
in 1984. ElGamal encryption is used in the free GNU Privacy Guard
software, recent versions of PGP
, and other cryptosystem
s. The Digital Signature Algorithm
is a variant of the ElGamal signature scheme
, which should not be confused with ElGamal encryption.
ElGamal encryption can be defined over any cyclic group
. Its security depends upon the difficulty of a certain problem in 
related to computing discrete logarithm
s (see below).
to Alice under her public key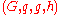 
,
The steps above can be computed ahead of time.
with her private key 
,
The decryption algorithm produces the intended message, since
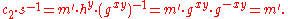
The ElGamal cryptosystem is usually used in a hybrid cryptosystem
. I.e., the message itself is encrypted using a symmetric cryptosystem and ElGamal is then used
to encrypt the key used for the symmetric cryptosystem. This allows encryption of messages that are longer than the size of the group
.
as well as any padding scheme used on the messages.
If the computational Diffie–Hellman assumption holds in the underlying cyclic group
, then the encryption function is one-way
.
If the decisional Diffie–Hellman assumption (DDH) holds in
, then
ElGamal achieves semantic security
. Semantic security is not implied by the computational Diffie–Hellman assumption alone. See decisional Diffie–Hellman assumption for a discussion of groups where the assumption is believed to hold.
ElGamal encryption is unconditionally malleable
, and therefore is not secure under chosen ciphertext attack. For example, given an encryption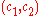
of some (possibly unknown) message 
, one can easily construct a valid encryption 
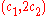of the message 
.
To achieve chosen-ciphertext security, the scheme must be further modified, or an appropriate padding scheme must be used. Depending on the modification, the DDH assumption may or may not be necessary.
Other schemes related to ElGamal which achieve security against chosen ciphertext attacks have also been proposed.
The Cramer–Shoup cryptosystem is secure under chosen ciphertext attack assuming DDH holds for
. Its proof does not use the random oracle model. Another proposed scheme is DHAES, whose proof requires an assumption that is weaker than the DDH assumption.
, meaning that a single plaintext
can be encrypted to many possible ciphertexts, with the consequence that a general ElGamal encryption produces a 2:1 expansion in size from plaintext to ciphertext.
Encryption under ElGamal requires two exponentiation
s; however, these exponentiations are independent of the message and can be computed ahead of time if need be. Decryption only requires one exponentiation:
can be avoided by using an alternative method for decryption.
To decrypt a ciphertext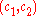
with Alice's private key 
,
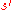is the inverse of 
. This is a consequence of Lagrange's theorem
, because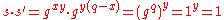
.
The decryption algorithm produces the intended message, since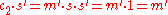
.
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, the ElGamal encryption system is an asymmetric key encryption algorithm for public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
which is based on the Diffie–Hellman key exchange. It was described by Taher Elgamal
Taher Elgamal
Dr. Taher Elgamal is an Egyptian cryptographer. Elgamal is sometimes written as El Gamal or ElGamal, but Elgamal is now preferred...
in 1984. ElGamal encryption is used in the free GNU Privacy Guard
GNU Privacy Guard
GNU Privacy Guard is a GPL Licensed alternative to the PGP suite of cryptographic software. GnuPG is compliant with RFC 4880, which is the current IETF standards track specification of OpenPGP...
software, recent versions of PGP
Pretty Good Privacy
Pretty Good Privacy is a data encryption and decryption computer program that provides cryptographic privacy and authentication for data communication. PGP is often used for signing, encrypting and decrypting texts, E-mails, files, directories and whole disk partitions to increase the security...
, and other cryptosystem
Cryptosystem
There are two different meanings of the word cryptosystem. One is used by the cryptographic community, while the other is the meaning understood by the public.- General meaning :...
s. The Digital Signature Algorithm
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
is a variant of the ElGamal signature scheme
ElGamal signature scheme
The ElGamal signature scheme is a digital signature scheme which is based on the difficulty of computing discrete logarithms. It was described by Taher ElGamal in 1984....
, which should not be confused with ElGamal encryption.
ElGamal encryption can be defined over any cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. Its security depends upon the difficulty of a certain problem in related to computing discrete logarithmDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s (see below).
The algorithm
ElGamal encryption consists of three components: the key generator, the encryption algorithm, and the decryption algorithm.Key generation
The key generator works as follows:- Alice generates an efficient description of a multiplicative cyclic group
of order 
with generatorGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
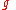. See below for a discussion on the required properties of this group. - Alice chooses a random
from 
. - Alice computes
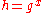. - Alice publishes
, along with the description of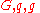 
, as her public key. Alice retains 
as her private key which must be kept secret.
Encryption
The encryption algorithm works as follows: to encrypt a message to Alice under her public key 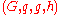,- Bob chooses a random
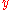from 
, then calculates 
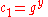. - Bob calculates the shared secret
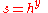. Since a new 
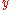is generated for every message, 
is also called an ephemeral keyEphemeral keyA cryptographic key is called ephemeral if it is generated for each execution of a key establishment process. In some cases ephemeral keys are used more than once, within a single session where the sender generates only one ephemeral key pair per message and the private key is combined separately...
.
The steps above can be computed ahead of time.
- Bob converts his secret message
into an element 
of 
. - Bob calculates
. - Bob sends the ciphertext
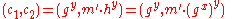to Alice.
Decryption
The decryption algorithm works as follows: to decrypt a ciphertext with her private key ,
- Alice calculates the shared secret
- and then computes
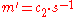which she then converts back into the plaintext message 
.
The decryption algorithm produces the intended message, since
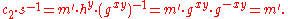
The ElGamal cryptosystem is usually used in a hybrid cryptosystem
Hybrid cryptosystem
In cryptography, public-key cryptosystems are convenient in that they do not require the sender and receiver to share a common secret in order to communicate securely . However, they often rely on complicated mathematical computations and are thus generally much more inefficient than comparable...
. I.e., the message itself is encrypted using a symmetric cryptosystem and ElGamal is then used
to encrypt the key used for the symmetric cryptosystem. This allows encryption of messages that are longer than the size of the group
.Security
The security of the ElGamal scheme depends on the properties of the underlying group as well as any padding scheme used on the messages.If the computational Diffie–Hellman assumption holds in the underlying cyclic group
, then the encryption function is one-wayOne-way function
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems...
.
If the decisional Diffie–Hellman assumption (DDH) holds in
, thenElGamal achieves semantic security
Semantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
. Semantic security is not implied by the computational Diffie–Hellman assumption alone. See decisional Diffie–Hellman assumption for a discussion of groups where the assumption is believed to hold.
ElGamal encryption is unconditionally malleable
Malleability (cryptography)
Malleability is a property of some cryptographic algorithms. An encryption algorithm is malleable if it is possible for an adversary to transform a ciphertext into another ciphertext which decrypts to a related plaintext...
, and therefore is not secure under chosen ciphertext attack. For example, given an encryption
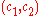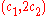of some (possibly unknown) message , one can easily construct a valid encryption of the message .To achieve chosen-ciphertext security, the scheme must be further modified, or an appropriate padding scheme must be used. Depending on the modification, the DDH assumption may or may not be necessary.
Other schemes related to ElGamal which achieve security against chosen ciphertext attacks have also been proposed.
The Cramer–Shoup cryptosystem is secure under chosen ciphertext attack assuming DDH holds for
. Its proof does not use the random oracle model. Another proposed scheme is DHAES, whose proof requires an assumption that is weaker than the DDH assumption.Efficiency
ElGamal encryption is probabilisticProbabilistic encryption
Probabilistic encryption is the use of randomness in an encryption algorithm, so that when encrypting the same message several times it will, in general, yield different ciphertexts...
, meaning that a single plaintext
Plaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
can be encrypted to many possible ciphertexts, with the consequence that a general ElGamal encryption produces a 2:1 expansion in size from plaintext to ciphertext.
Encryption under ElGamal requires two exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
s; however, these exponentiations are independent of the message and can be computed ahead of time if need be. Decryption only requires one exponentiation:
Decryption
The division by can be avoided by using an alternative method for decryption.To decrypt a ciphertext
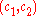with Alice's private key ,
- Alice calculates
.
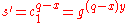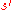is the inverse of . This is a consequence of Lagrange's theoremLagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, because
.
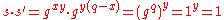- Alice then computes
, which she then converts back into the plaintext message 
.
The decryption algorithm produces the intended message, since
.
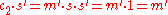