Nuclear magnetic resonance in porous media
Encyclopedia
Nuclear magnetic resonance (NMR) in porous media covers the application of using NMR
as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity
and pore size distribution, the permeability, the water saturation, the wettability, etc. An example of this is the development of the NMR well logging device for measuring nuclear magnetic properties of fluids in underground porous sediments.
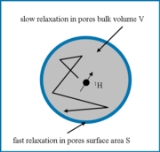
in a porous media may be divided into two regions; surface
area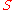 and bulk volume
and bulk volume  (Figure 1).
(Figure 1).
 The surface area is a thin layer with thickness
The surface area is a thin layer with thickness  of a few molecules close to the pore wall surface. The bulk volume is the remaining part of the pore volume and usually dominates the overall pore volume
of a few molecules close to the pore wall surface. The bulk volume is the remaining part of the pore volume and usually dominates the overall pore volume
. With respect to NMR excitations of nuclear states for hydrogen
-containing molecules in these regions, different relaxation times for the induced excited energy states are expected. The relaxation time is significantly shorter for a molecule in the surface area, compared to a molecule in the bulk volume. This is an effect of paramagnetic centres in the pore wall surface that causes the relaxation time to be faster.
The inverse of the relaxation time , is expressed by contributions from the bulk volume
, is expressed by contributions from the bulk volume  , the surface area
, the surface area 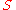 and the self-diffusion
and the self-diffusion
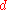 :
: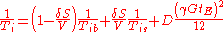 with
with 
where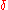 is the thickness of the surface area,
is the thickness of the surface area, 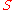 is the surface area,
is the surface area,  is the pore volume,
is the pore volume,  is the relaxation time in the bulk volume,
is the relaxation time in the bulk volume,  is the relaxation time for the surface,
is the relaxation time for the surface, 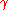 is the gyromagnetic ratio,
is the gyromagnetic ratio,  is the magnetic field
is the magnetic field
gradient (assumed to be constant), is the time between echoes and
is the time between echoes and  is the self-diffusion
is the self-diffusion
coefficient of the fluid. The surface relaxation can be assumed as uniform or non-uniform.
The NMR signal intensity in the distribution plot reflected by the measured amplitude of the NMR signal is proportional to the total amount of hydrogen nuclei, while the relaxation time depends on the interaction between the nuclear spins and the surroundings. In a characteristic pore containing e.g. water, the bulk water exhibits a single exponential decay. The water close to the pore wall surface exhibits faster
distribution plot reflected by the measured amplitude of the NMR signal is proportional to the total amount of hydrogen nuclei, while the relaxation time depends on the interaction between the nuclear spins and the surroundings. In a characteristic pore containing e.g. water, the bulk water exhibits a single exponential decay. The water close to the pore wall surface exhibits faster 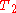 relaxation time for this characteristic pore size
relaxation time for this characteristic pore size
measured relaxation spectra with surface-to-volume ratios of pores, and the latter is used to estimate permeability. The common approach is based on the model proposed by Brownstein and Tarr. They have shown that, in the fast diffusion limit, given by the expression: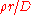
where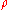 is the surface relaxivity of pore wall material,
is the surface relaxivity of pore wall material,  is the radius of the spherical pore and
is the radius of the spherical pore and  is the bulk diffusivity. The connection between NMR relaxation measurements and petrophysical
is the bulk diffusivity. The connection between NMR relaxation measurements and petrophysical
parameters such as permeability stems from the strong effect that the rock
surface has on promoting magnetic relaxation. For a single pore, the magnetic decay as a function of time is described by a single exponential: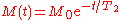
where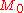 is the initial magnetization
is the initial magnetization
and the transverse relaxation time is given by:
is given by: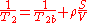
 is the surface-to-volume ratio of the pore,
is the surface-to-volume ratio of the pore, 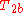 is bulk relaxation time of the fluid that fills the pore space, and
is bulk relaxation time of the fluid that fills the pore space, and 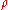 is the surface relaxation strength. For small pores or large
is the surface relaxation strength. For small pores or large  , the bulk relaxation time is small and the equation can be approximated by:
, the bulk relaxation time is small and the equation can be approximated by: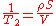
Real rocks contain an assembly of interconnected pores of different sizes. The pores are connected through small and narrow pore throats (i.e. links) that restrict interpore diffusion
. If interpore diffusion is negligible, each pore can be considered to be distinct and the magnetization within individual pores decays independently of the magnetization in neighbouring pores. The decay can thus be described as:
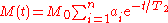
where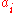 is the volume fraction of pores of size
is the volume fraction of pores of size 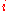 that decays with relaxation time
that decays with relaxation time 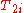 . The multi-exponential representation corresponds to a division of the pore space into
. The multi-exponential representation corresponds to a division of the pore space into  main groups based on
main groups based on  (surface-to-volume ratio) values. Due to the pore size variations, a non-linear optimization algorithm with multi-exponential terms is used to fit experimental data. Usually, a weighted geometric mean
(surface-to-volume ratio) values. Due to the pore size variations, a non-linear optimization algorithm with multi-exponential terms is used to fit experimental data. Usually, a weighted geometric mean
,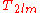 , of the relaxation times is used for permeability correlations:
, of the relaxation times is used for permeability correlations:

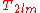 is thus related to an average
is thus related to an average  or pore size. Commonly used NMR permeability correlations as proposed by Dunn et al. are of the form:
or pore size. Commonly used NMR permeability correlations as proposed by Dunn et al. are of the form:

where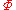 is the porosity
is the porosity
of the rock. The exponents and
and  are usually taken as four and two, respectively. Correlations of this form can be rationalized from the Kozeny–Carman equation:
are usually taken as four and two, respectively. Correlations of this form can be rationalized from the Kozeny–Carman equation:

by assuming that the tortuosity
 is proportional to
is proportional to 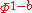 . However, it is well known that tortuosity is not only a function of porosity. It also depends on the formation factor
. However, it is well known that tortuosity is not only a function of porosity. It also depends on the formation factor 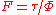 . The formation factor can be obtained from resistivity logs and is usually readily available. This has given rise to permeability correlations of the form:
. The formation factor can be obtained from resistivity logs and is usually readily available. This has given rise to permeability correlations of the form:
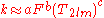
Standard values for the exponents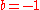 and
and  , respectively. Intuitively, correlations of this form are a better model since it incorporates tortuosity information through
, respectively. Intuitively, correlations of this form are a better model since it incorporates tortuosity information through  .
.
The value of the surface relaxation strength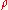 affects strongly the NMR signal decay rate and hence the estimated permeability. Surface relaxivity data are difficult to measure, and most NMR permeability correlations assume a constant
affects strongly the NMR signal decay rate and hence the estimated permeability. Surface relaxivity data are difficult to measure, and most NMR permeability correlations assume a constant  . However, for heterogeneous reservoir rocks with different mineralogy
. However, for heterogeneous reservoir rocks with different mineralogy
,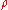 is certainly not constant and surface relaxivity has been reported to increase with higher fractions of microporosity. If surface relaxivity data are available it can be included in the NMR permeability correlation as
is certainly not constant and surface relaxivity has been reported to increase with higher fractions of microporosity. If surface relaxivity data are available it can be included in the NMR permeability correlation as

For fully brine
saturated porous media, three different mechanisms contribute to the relaxation: bulk fluid relaxation, surface relaxation, and relaxation due to gradients in the magnetic field. In the absence of magnetic field gradients, the equations describing the relaxation are:

 on S
on S
with the initial condition
 and
and 
where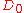 is the self-diffusion coefficient. The governing diffusion equation can be solved by a 3D random walk algorithm
is the self-diffusion coefficient. The governing diffusion equation can be solved by a 3D random walk algorithm
. Initially, the walkers are launched at random positions in the pore space. At each time step,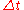 , they advance from their current position,
, they advance from their current position, 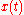 , to a new position,
, to a new position,  , by taking steps of fixed length
, by taking steps of fixed length  in a randomly chosen direction. The time step is given by:
in a randomly chosen direction. The time step is given by:
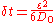
The new position is given by

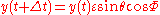
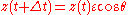
The angles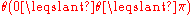 and
and  represent the randomly selected direction for each random walker in spherical coordinates. It can be noted that
represent the randomly selected direction for each random walker in spherical coordinates. It can be noted that 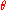 must be distributed uniformly
must be distributed uniformly
in the range (0, ). If a walker encounters a pore-solid interface, it is killed with a finite probability
). If a walker encounters a pore-solid interface, it is killed with a finite probability 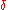 . The killing probability
. The killing probability 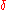 is related to the surface relaxation strength by:
is related to the surface relaxation strength by:

If the walker survives, it simply bounces off the interface and its position does not change. At each time step, the fraction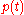 of the initial walkers that are still alive is recorded. Since the walkers move with equal probability in all directions, the above algorithm is valid as long as there is no magnetic gradient in the system.
of the initial walkers that are still alive is recorded. Since the walkers move with equal probability in all directions, the above algorithm is valid as long as there is no magnetic gradient in the system.
When protons are diffusing, the sequence of spin echo amplitudes is affected by inhomogeneities in the permanent magnetic field. This results in an additional decay of the spin echo amplitudes that depends on the echo spacing . In the simple case of a uniform spatial gradient
. In the simple case of a uniform spatial gradient  , the additional decay can be expressed as a multiplicative factor:
, the additional decay can be expressed as a multiplicative factor:
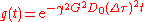
where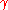 is the ratio of the Larmor frequency
is the ratio of the Larmor frequency
to the magnetic field intensity. The total magnetization amplitude as a function of time is then given as:

conditions in a porous media containing two or more immiscible fluid phases determine the microscopic fluid distribution in the pore network. Nuclear magnetic resonance measurements are sensitive to wettability because of the strong effect that the solid surface has on promoting magnetic relaxation of the saturating fluid. The idea of using NMR as a tool to measure wettability was presented by Brown and Fatt in 1956. The magnitude of this effect depends upon the wettability characteristics of the solid with respect to the liquid in contact with the surface. Their theory is based on the hypothesis that molecular movements are slower in the bulk liquid than at the solid-liquid interface. In this solid-liquid interface the diffusion coefficient is reduced, which correspond to a zone of higher viscosity. In this higher viscosity zone, the magnetically aligned protons can more easily transfer their energy to their surroundings. The magnitude of this effect depends upon the wettability characteristics of the solid with respect to the liquid in contact with the surface.
: small crystals of a liquid in the pores melt at a lower temperature than the bulk liquid : The melting point depression is inversely proportional to the pore size. The technique is closely related to that of the use of gas adsorption to measure pore sizes (Kelvin equation
). Both techniques are particular cases of the Gibbs Equations (Josiah Willard Gibbs
): the Kelvin Equation is the constant temperature case, and the Gibbs-Thomson Equation is the constant pressure case.
To make a Cryoporometry measurement, a liquid is imbibed into the porous sample, the sample cooled until all the liquid is frozen, and then warmed slowly while measuring the quantity of the liquid that has melted. Thus it is similar to DSC thermoporosimetry, but has higher resolution, as the signal detection does not rely on transient heat flows, and the measurement can be made arbitrarily slowly. It is suitable for measuring pore diameters in the range 2 nm–2 μm.
Nuclear Magnetic Resonance
(NMR) may be used as a convenient method of measuring the quantity of liquid that has melted, as a function of temperature, making use of the fact that the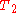 relaxation time in a frozen material is usually much shorter than that in a mobile liquid. The technique was developed at the University of Kent in the UK.
relaxation time in a frozen material is usually much shorter than that in a mobile liquid. The technique was developed at the University of Kent in the UK.
It is also possible to adapt the basic NMRC experiment to provide structural resolution in spatially-dependent pore size distributions, or to provide behavioural information about the confined liquid.
NMR
NMR may refer to:Applications of Nuclear Magnetic Resonance:* Nuclear magnetic resonance* NMR spectroscopy* Solid-state nuclear magnetic resonance* Protein nuclear magnetic resonance spectroscopy* Proton NMR* Carbon-13 NMR...
as a tool to study the structure of porous media and various processes occurring in them. This technique allows the determination of characteristics such as the porosity
Porosity
Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%...
and pore size distribution, the permeability, the water saturation, the wettability, etc. An example of this is the development of the NMR well logging device for measuring nuclear magnetic properties of fluids in underground porous sediments.
Theory of relaxation time distribution in porous media
Microscopically the volume of a single porePorosity
Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%...
in a porous media may be divided into two regions; surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
area
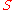 and bulk volume
and bulk volume  (Figure 1).
(Figure 1).
 of a few molecules close to the pore wall surface. The bulk volume is the remaining part of the pore volume and usually dominates the overall pore volume
of a few molecules close to the pore wall surface. The bulk volume is the remaining part of the pore volume and usually dominates the overall pore volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
. With respect to NMR excitations of nuclear states for hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
-containing molecules in these regions, different relaxation times for the induced excited energy states are expected. The relaxation time is significantly shorter for a molecule in the surface area, compared to a molecule in the bulk volume. This is an effect of paramagnetic centres in the pore wall surface that causes the relaxation time to be faster.
The inverse of the relaxation time
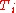 , is expressed by contributions from the bulk volume
, is expressed by contributions from the bulk volume  , the surface area
, the surface area 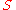 and the self-diffusion
and the self-diffusionSelf-diffusion
According to IUPAC definition, self-diffusion coefficient is the diffusion coefficient D_i^* of species i when the chemical potential gradient equals zero. It is linked to the diffusion coefficient D_i by the equation:...
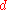 :
: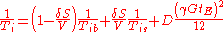 with
with 
where
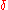 is the thickness of the surface area,
is the thickness of the surface area, 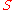 is the surface area,
is the surface area,  is the pore volume,
is the pore volume,  is the relaxation time in the bulk volume,
is the relaxation time in the bulk volume,  is the relaxation time for the surface,
is the relaxation time for the surface, 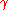 is the gyromagnetic ratio,
is the gyromagnetic ratio,  is the magnetic field
is the magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
gradient (assumed to be constant),
 is the time between echoes and
is the time between echoes and  is the self-diffusion
is the self-diffusionSelf-diffusion
According to IUPAC definition, self-diffusion coefficient is the diffusion coefficient D_i^* of species i when the chemical potential gradient equals zero. It is linked to the diffusion coefficient D_i by the equation:...
coefficient of the fluid. The surface relaxation can be assumed as uniform or non-uniform.
The NMR signal intensity in the
 distribution plot reflected by the measured amplitude of the NMR signal is proportional to the total amount of hydrogen nuclei, while the relaxation time depends on the interaction between the nuclear spins and the surroundings. In a characteristic pore containing e.g. water, the bulk water exhibits a single exponential decay. The water close to the pore wall surface exhibits faster
distribution plot reflected by the measured amplitude of the NMR signal is proportional to the total amount of hydrogen nuclei, while the relaxation time depends on the interaction between the nuclear spins and the surroundings. In a characteristic pore containing e.g. water, the bulk water exhibits a single exponential decay. The water close to the pore wall surface exhibits faster 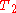 relaxation time for this characteristic pore size
relaxation time for this characteristic pore sizeNMR permeability correlations
NMR techniques are typically used to predict permeability for fluid typing and to obtain formation porosity, which is independent of mineralogy. The former application uses a surface-relaxation mechanism to relatemeasured relaxation spectra with surface-to-volume ratios of pores, and the latter is used to estimate permeability. The common approach is based on the model proposed by Brownstein and Tarr. They have shown that, in the fast diffusion limit, given by the expression:
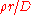
where
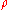 is the surface relaxivity of pore wall material,
is the surface relaxivity of pore wall material,  is the radius of the spherical pore and
is the radius of the spherical pore and  is the bulk diffusivity. The connection between NMR relaxation measurements and petrophysical
is the bulk diffusivity. The connection between NMR relaxation measurements and petrophysicalPetrophysics
Petrophysics is the study of the physical and chemical properties that describe the occurrence and behavior of rocks, soils and fluids . Petrophysics mainly studies reservoirs of resources, including ore deposits and oil or natural gas reservoirs...
parameters such as permeability stems from the strong effect that the rock
Rock (geology)
In geology, rock or stone is a naturally occurring solid aggregate of minerals and/or mineraloids.The Earth's outer solid layer, the lithosphere, is made of rock. In general rocks are of three types, namely, igneous, sedimentary, and metamorphic...
surface has on promoting magnetic relaxation. For a single pore, the magnetic decay as a function of time is described by a single exponential:
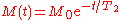
where
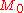 is the initial magnetization
is the initial magnetizationMagnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
and the transverse relaxation time
 is given by:
is given by: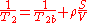
 is the surface-to-volume ratio of the pore,
is the surface-to-volume ratio of the pore, 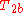 is bulk relaxation time of the fluid that fills the pore space, and
is bulk relaxation time of the fluid that fills the pore space, and 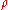 is the surface relaxation strength. For small pores or large
is the surface relaxation strength. For small pores or large  , the bulk relaxation time is small and the equation can be approximated by:
, the bulk relaxation time is small and the equation can be approximated by: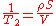
Real rocks contain an assembly of interconnected pores of different sizes. The pores are connected through small and narrow pore throats (i.e. links) that restrict interpore diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
. If interpore diffusion is negligible, each pore can be considered to be distinct and the magnetization within individual pores decays independently of the magnetization in neighbouring pores. The decay can thus be described as:
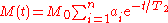
where
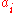 is the volume fraction of pores of size
is the volume fraction of pores of size 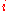 that decays with relaxation time
that decays with relaxation time 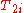 . The multi-exponential representation corresponds to a division of the pore space into
. The multi-exponential representation corresponds to a division of the pore space into  main groups based on
main groups based on  (surface-to-volume ratio) values. Due to the pore size variations, a non-linear optimization algorithm with multi-exponential terms is used to fit experimental data. Usually, a weighted geometric mean
(surface-to-volume ratio) values. Due to the pore size variations, a non-linear optimization algorithm with multi-exponential terms is used to fit experimental data. Usually, a weighted geometric meanGeometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
,
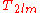 , of the relaxation times is used for permeability correlations:
, of the relaxation times is used for permeability correlations:
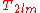 is thus related to an average
is thus related to an average  or pore size. Commonly used NMR permeability correlations as proposed by Dunn et al. are of the form:
or pore size. Commonly used NMR permeability correlations as proposed by Dunn et al. are of the form:
where
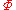 is the porosity
is the porosityPorosity
Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%...
of the rock. The exponents
 and
and  are usually taken as four and two, respectively. Correlations of this form can be rationalized from the Kozeny–Carman equation:
are usually taken as four and two, respectively. Correlations of this form can be rationalized from the Kozeny–Carman equation:
by assuming that the tortuosity
Tortuosity
Tortuosity is a property of curve being tortuous . There have been several attempts to quantify this property. Tortuosity is commonly used to describe diffusion in porous media...
 is proportional to
is proportional to 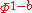 . However, it is well known that tortuosity is not only a function of porosity. It also depends on the formation factor
. However, it is well known that tortuosity is not only a function of porosity. It also depends on the formation factor 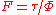 . The formation factor can be obtained from resistivity logs and is usually readily available. This has given rise to permeability correlations of the form:
. The formation factor can be obtained from resistivity logs and is usually readily available. This has given rise to permeability correlations of the form: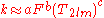
Standard values for the exponents
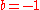 and
and  , respectively. Intuitively, correlations of this form are a better model since it incorporates tortuosity information through
, respectively. Intuitively, correlations of this form are a better model since it incorporates tortuosity information through  .
.The value of the surface relaxation strength
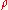 affects strongly the NMR signal decay rate and hence the estimated permeability. Surface relaxivity data are difficult to measure, and most NMR permeability correlations assume a constant
affects strongly the NMR signal decay rate and hence the estimated permeability. Surface relaxivity data are difficult to measure, and most NMR permeability correlations assume a constant  . However, for heterogeneous reservoir rocks with different mineralogy
. However, for heterogeneous reservoir rocks with different mineralogyMineralogy
Mineralogy is the study of chemistry, crystal structure, and physical properties of minerals. Specific studies within mineralogy include the processes of mineral origin and formation, classification of minerals, their geographical distribution, as well as their utilization.-History:Early writing...
,
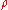 is certainly not constant and surface relaxivity has been reported to increase with higher fractions of microporosity. If surface relaxivity data are available it can be included in the NMR permeability correlation as
is certainly not constant and surface relaxivity has been reported to increase with higher fractions of microporosity. If surface relaxivity data are available it can be included in the NMR permeability correlation as
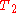 relaxation
relaxation
For fully brineBrine
Brine is water, saturated or nearly saturated with salt .Brine is used to preserve vegetables, fruit, fish, and meat, in a process known as brining . Brine is also commonly used to age Halloumi and Feta cheeses, or for pickling foodstuffs, as a means of preserving them...
saturated porous media, three different mechanisms contribute to the relaxation: bulk fluid relaxation, surface relaxation, and relaxation due to gradients in the magnetic field. In the absence of magnetic field gradients, the equations describing the relaxation are:

 on S
on Swith the initial condition
 and
and 
where
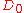 is the self-diffusion coefficient. The governing diffusion equation can be solved by a 3D random walk algorithm
is the self-diffusion coefficient. The governing diffusion equation can be solved by a 3D random walk algorithmRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
. Initially, the walkers are launched at random positions in the pore space. At each time step,
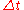 , they advance from their current position,
, they advance from their current position, 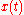 , to a new position,
, to a new position,  , by taking steps of fixed length
, by taking steps of fixed length  in a randomly chosen direction. The time step is given by:
in a randomly chosen direction. The time step is given by: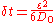
The new position is given by

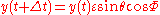
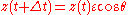
The angles
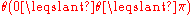 and
and  represent the randomly selected direction for each random walker in spherical coordinates. It can be noted that
represent the randomly selected direction for each random walker in spherical coordinates. It can be noted that 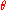 must be distributed uniformly
must be distributed uniformlyUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
in the range (0,
 ). If a walker encounters a pore-solid interface, it is killed with a finite probability
). If a walker encounters a pore-solid interface, it is killed with a finite probability 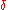 . The killing probability
. The killing probability 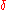 is related to the surface relaxation strength by:
is related to the surface relaxation strength by:
If the walker survives, it simply bounces off the interface and its position does not change. At each time step, the fraction
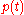 of the initial walkers that are still alive is recorded. Since the walkers move with equal probability in all directions, the above algorithm is valid as long as there is no magnetic gradient in the system.
of the initial walkers that are still alive is recorded. Since the walkers move with equal probability in all directions, the above algorithm is valid as long as there is no magnetic gradient in the system.When protons are diffusing, the sequence of spin echo amplitudes is affected by inhomogeneities in the permanent magnetic field. This results in an additional decay of the spin echo amplitudes that depends on the echo spacing
 . In the simple case of a uniform spatial gradient
. In the simple case of a uniform spatial gradient  , the additional decay can be expressed as a multiplicative factor:
, the additional decay can be expressed as a multiplicative factor: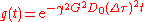
where
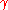 is the ratio of the Larmor frequency
is the ratio of the Larmor frequencyLarmor precession
In physics, Larmor precession is the precession of the magnetic moments of electrons, atomic nuclei, and atoms about an external magnetic field...
to the magnetic field intensity. The total magnetization amplitude as a function of time is then given as:

NMR as a tool to measure wettability
The wettabilityWetting
Wetting is the ability of a liquid to maintain contact with a solid surface, resulting from intermolecular interactions when the two are brought together. The degree of wetting is determined by a force balance between adhesive and cohesive forces.Wetting is important in the bonding or adherence of...
conditions in a porous media containing two or more immiscible fluid phases determine the microscopic fluid distribution in the pore network. Nuclear magnetic resonance measurements are sensitive to wettability because of the strong effect that the solid surface has on promoting magnetic relaxation of the saturating fluid. The idea of using NMR as a tool to measure wettability was presented by Brown and Fatt in 1956. The magnitude of this effect depends upon the wettability characteristics of the solid with respect to the liquid in contact with the surface. Their theory is based on the hypothesis that molecular movements are slower in the bulk liquid than at the solid-liquid interface. In this solid-liquid interface the diffusion coefficient is reduced, which correspond to a zone of higher viscosity. In this higher viscosity zone, the magnetically aligned protons can more easily transfer their energy to their surroundings. The magnitude of this effect depends upon the wettability characteristics of the solid with respect to the liquid in contact with the surface.
NMR Cryoporometry for measuring pore size distributions
NMR Cryoporometry (NMRC) is a recent technique for measuring total porosity and pore size distributions. It makes use of the Gibbs-Thomson effectGibbs-Thomson effect
The Gibbs–Thomson effect relates surface curvature to vapor pressure and chemical potential and is a consequence of surface tension. It is named after Josiah Willard Gibbs and William Thomson, 1st Baron Kelvin. It leads to the fact that small liquid droplets The Gibbs–Thomson effect (also called...
: small crystals of a liquid in the pores melt at a lower temperature than the bulk liquid : The melting point depression is inversely proportional to the pore size. The technique is closely related to that of the use of gas adsorption to measure pore sizes (Kelvin equation
Kelvin equation
The Kelvin equation describes the change in vapour pressure due to a curved liquid/vapor interface with radius r . The Kelvin equation is used for determination of pore size distribution of a porous medium using adsorption porosimetry...
). Both techniques are particular cases of the Gibbs Equations (Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
): the Kelvin Equation is the constant temperature case, and the Gibbs-Thomson Equation is the constant pressure case.
To make a Cryoporometry measurement, a liquid is imbibed into the porous sample, the sample cooled until all the liquid is frozen, and then warmed slowly while measuring the quantity of the liquid that has melted. Thus it is similar to DSC thermoporosimetry, but has higher resolution, as the signal detection does not rely on transient heat flows, and the measurement can be made arbitrarily slowly. It is suitable for measuring pore diameters in the range 2 nm–2 μm.
Nuclear Magnetic Resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
(NMR) may be used as a convenient method of measuring the quantity of liquid that has melted, as a function of temperature, making use of the fact that the
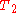 relaxation time in a frozen material is usually much shorter than that in a mobile liquid. The technique was developed at the University of Kent in the UK.
relaxation time in a frozen material is usually much shorter than that in a mobile liquid. The technique was developed at the University of Kent in the UK.It is also possible to adapt the basic NMRC experiment to provide structural resolution in spatially-dependent pore size distributions, or to provide behavioural information about the confined liquid.

