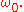Nonlinear resonance
Encyclopedia
In physics
, nonlinear resonance is the occurrence of resonance
in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes
– depends on the amplitude
of the oscillation
s, while for linear system
s this is independent of amplitude.
coincides with the eigen-frequency of the system or not (linear and nonlinear resonance correspondingly). The frequency condition of nonlinear resonance reads

with possibly different being eigen-frequencies of the linear part of some nonlinear partial differential equation
being eigen-frequencies of the linear part of some nonlinear partial differential equation
. Here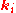 is a vector
is a vector
with the integer subscripts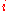 being indexes into Fourier harmonics – or eigenmodes – see Fourier series
being indexes into Fourier harmonics – or eigenmodes – see Fourier series
. Accordingly, the frequency resonance condition is equivalent to a Diophantine equation
with many unknowns. The problem of finding their solutions is equivalent to the Hilbert's tenth problem
that is proven to be algorithmically unsolvable.
Main notions and results of the theory of nonlinear resonances are:
Nonlinear effects
may significantly modify the shape of the resonance
curves of harmonic oscillator
s.
First of all, the resonance frequency is shifted from its "natural" value
is shifted from its "natural" value 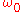 according to the formula
according to the formula

where is the oscillation amplitude and
is the oscillation amplitude and  is a constant defined by the anharmonic coefficients.
is a constant defined by the anharmonic coefficients.
Second, the shape of the resonance curve is distorted (foldover effect). When the amplitude of the (sinusoidal) external force reaches a critical value
reaches a critical value 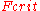 instabilities appear. The critical value is given by the formula
instabilities appear. The critical value is given by the formula
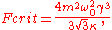
where is the oscillator mass and
is the oscillator mass and 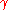 is the damping coefficient.
is the damping coefficient.
Furthermore, new resonances appear in which oscillations of frequency close to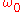 are excited by an external force with frequency quite different from
are excited by an external force with frequency quite different from 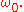
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, nonlinear resonance is the occurrence of resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequencies and modes
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
– depends on the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s, while for linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s this is independent of amplitude.
Description
Generically two types of resonances have to be distinguished – linear and nonlinear. From the physical point of view, they are defined by the fact whether or not external forceForce
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
coincides with the eigen-frequency of the system or not (linear and nonlinear resonance correspondingly). The frequency condition of nonlinear resonance reads

with possibly different
 being eigen-frequencies of the linear part of some nonlinear partial differential equation
being eigen-frequencies of the linear part of some nonlinear partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. Here
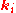 is a vector
is a vectorVector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
with the integer subscripts
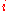 being indexes into Fourier harmonics – or eigenmodes – see Fourier series
being indexes into Fourier harmonics – or eigenmodes – see Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. Accordingly, the frequency resonance condition is equivalent to a Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
with many unknowns. The problem of finding their solutions is equivalent to the Hilbert's tenth problem
Hilbert's tenth problem
Hilbert's tenth problem is the tenth on the list of Hilbert's problems of 1900. Its statement is as follows:Given a Diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined in a finite...
that is proven to be algorithmically unsolvable.
Main notions and results of the theory of nonlinear resonances are:
- The use of the special form of dispersion functionsDispersion relationIn physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
 appearing in various physical applications allows to find the solutions of frequency resonance condition.
appearing in various physical applications allows to find the solutions of frequency resonance condition. - The set of resonances for given dispersion function and the form of resonance conditions is partitioned into non-intersecting resonance clusters; dynamics of each cluster can be studied independently (at the appropriate time-scale).
- Each resonance cluster can be represented by its NR-diagram which is a plane graph of the special structure. This representation allows to reconstruct uniquely 3a) dynamical system describing time-dependent behavior of the cluster, and 3b) the set of its polynomial conservation laws which are generalization of Manley–Rowe constants of motion for the simplest clusters (triads and quartets)
- Dynamical systems describing some types of the clusters can be solved analytically.
- These theoretical results can be used directly for describing real-life physical phenomena (e.g. intraseasonal oscillations in the Earth's atmosphere) or various wave turbulent regimes in the theory of wave turbulenceWave turbulenceWave turbulence is a set of waves deviated far from thermal equilibrium. Such state is accompanied by dissipation. It is either decaying turbulence or requires external source of energy to sustain it...
.
Nonlinear resonance shift
Nonlinear effects
Anharmonicity
In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in simple harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be...
may significantly modify the shape of the resonance
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
curves of harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s.
First of all, the resonance frequency
 is shifted from its "natural" value
is shifted from its "natural" value 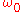 according to the formula
according to the formula
where
 is the oscillation amplitude and
is the oscillation amplitude and  is a constant defined by the anharmonic coefficients.
is a constant defined by the anharmonic coefficients.Second, the shape of the resonance curve is distorted (foldover effect). When the amplitude of the (sinusoidal) external force
 reaches a critical value
reaches a critical value 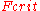 instabilities appear. The critical value is given by the formula
instabilities appear. The critical value is given by the formula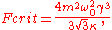
where
 is the oscillator mass and
is the oscillator mass and 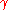 is the damping coefficient.
is the damping coefficient.Furthermore, new resonances appear in which oscillations of frequency close to
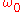 are excited by an external force with frequency quite different from
are excited by an external force with frequency quite different from