Nilmanifold
Encyclopedia
In mathematics
, a nilmanifold is a differentiable manifold
which has a transitive nilpotent
group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space
and is diffeomorphic to the quotient space
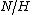, the quotient of a nilpotent Lie group
N modulo a closed subgroup
H. This notion was introduced by A. Mal'cev
in 1951.
In the Riemannian category, there is also a good notion of a nilmanifold. A Riemannian manifold
is called a homogeneous nilmanifold if there exist a nilpotent group of isometries acting transitively on it. The requirement that the transitive nilpotent group acts by isometries leads to the following rigid characterization: every homogeneous nilmanifold is isometric to a nilpotent Lie group with left-invariant metric (see Wilson ).
Nilmanifolds are important geometric objects and often arise as concrete examples with interesting properties; in Riemannian geometry these spaces always have mixed curvature, almost flat spaces arise as quotients of nilmanifolds, and compact nilmanifolds have been used to construct elementary examples of collapse of Riemannian metrics under the Ricci flow.
In addition to their role in geometry, nilmanifolds are increasingly being seen as having a role in arithmetic combinatorics
(see Green-Tao ) and ergodic theory
(see, e.g., Host-Kra ).
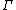. If the subgroup 
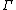acts cocompactly (via right multiplication) on N, then the quotient manifold 
will be a compact nilmanifold. As Mal'cev has shown, every compact
nilmanifold is obtained this way.
Such a subgroup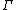
as above is called a lattice in N. It is well known that a nilpotent Lie group admits a lattice if and only if its Lie algebra admits a basis with rational structure constants: this is Malcev's criterion. Not all nilpotent Lie group admit lattices; for more details, see also Raghunathan.
A compact Riemannian nilmanifold is a compact Riemannian manifold which is locally isometric to a nilpotent Lie group with left-invariant metric. These spaces are constructed as follows. Let
be a lattice in a simply connected nilpotent Lie group N, as above. Endow N with a left-invariant (Riemannian) metric. Then the subgroup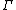 
acts by isometries on N via left-multiplication. Thus the quotient 
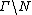is a compact space locally isometric to N. Note: this space is naturally diffeomorphic to 
.
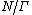Compact nilmanifolds also arise as principal bundles. For example, consider a 2-step nilpotent Lie group N which admits a lattice (see above). Let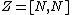
be the commutator subgroup of N. Denote by p the dimension of Z and by q the codimension of Z; i.e. the dimension of N is p+q. It is known (see Raghunathan) that 
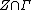is a lattice in Z. Hence, 
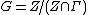is a p-dimensional compact torus. Since Z is central in N, the group G acts on the compact nilmanifold 
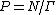with quotient space 
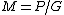. This base manifold M is a q-dimensional compact torus. It has been shown that ever principal torus bundle over a torus is of this form, see . More generally, a compact nilmanifold is torus bundle, over a torus bundle, over...over a torus.
As mentioned above, almost flat manifolds are intimately compact nilmanifolds. See that article for more information.
a cocompact lattice. An example of such a nilmanifold is an Iwasawa manifold
. From the 1980s, another (more general) notion of a complex nilmanifold gradually replaced this one.
An almost complex structure on a real Lie algebra g is an endomorphism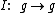
which squares to
-Idg. This operator is called a complex structure if its eigenspaces, corresponding to eigenvalues
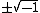, are subalgebras in 
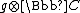. In this case, I defines a left-invariant complex structure on the corresponding Lie group. Such a manifold (G,I) is called a complex group manifold.
It is easy to see that every connected complex homogeneous manifold
equipped with a free, transitive, holomorphic action by a real Lie group is obtained this way.
Let G be a real, nilpotent Lie group. A complex nilmanifold is a quotient of a complex group manifold (G,I),
equipped with a left-invariant complex structure, by a discrete, cocompact lattice, acting from the right.
Complex nilmanifolds are usually not homogeneous, as complex varieties.
In complex dimension 2, the only complex nilmanifolds are a complex torus and a Kodaira surface
.
admit a Kähler structure (see also ).
Topologically, all nilmanifolds can be obtained
as iterated torus bundles over a torus. This is easily seen from a filtration by ascending central series.
For example, the Heisenberg group is a 2-step nilpotent Lie group. This nilpotent Lie group is also special in that it admits a compact quotient. The group
would be the upper triangular matrices with integral coefficients. The resulting nilmanifold is 3-dimensional. One possible fundamental domain
is (isomorphic to) [0,1]3 with the faces identified in a suitable way. This is because an element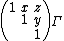
of the nilmanifold can be represented by the element 
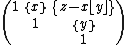in the fundamental domain. Here 
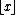denotes the floor function
of x, and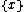
the fractional part. The appearance of the floor function here is a clue to the relevance of nilmanifolds to additive combinatorics: the so-called bracket polynomials, or generalised polynomials, seem to be important in the development of higher-order Fourier analysis.
. Another familiar example might be the compact 2-torus or Euclidean space under addition.
Lie groups produces a class of spaces called solvmanifolds. An important example of a solvmanifolds are Inoue surface
s, known in complex geometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a nilmanifold is a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
which has a transitive nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
and is diffeomorphic to the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
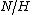, the quotient of a nilpotent Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
N modulo a closed subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H. This notion was introduced by A. Mal'cev
Anatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
in 1951.
In the Riemannian category, there is also a good notion of a nilmanifold. A Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
is called a homogeneous nilmanifold if there exist a nilpotent group of isometries acting transitively on it. The requirement that the transitive nilpotent group acts by isometries leads to the following rigid characterization: every homogeneous nilmanifold is isometric to a nilpotent Lie group with left-invariant metric (see Wilson ).
Nilmanifolds are important geometric objects and often arise as concrete examples with interesting properties; in Riemannian geometry these spaces always have mixed curvature, almost flat spaces arise as quotients of nilmanifolds, and compact nilmanifolds have been used to construct elementary examples of collapse of Riemannian metrics under the Ricci flow.
In addition to their role in geometry, nilmanifolds are increasingly being seen as having a role in arithmetic combinatorics
Arithmetic combinatorics
Arithmetic combinatorics arose out of the interplay between number theory, combinatorics, ergodic theory and harmonic analysis. It is about combinatorial estimates associated with arithmetic operations...
(see Green-Tao ) and ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
(see, e.g., Host-Kra ).
Compact nilmanifolds
A compact nilmanifold is a nilmanifold which is compact. One way to construct such spaces is to start with a simply connected nilpotent Lie group N and a discrete subgroup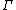. If the subgroup 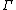acts cocompactly (via right multiplication) on N, then the quotient manifold will be a compact nilmanifold. As Mal'cev has shown, every compactnilmanifold is obtained this way.
Such a subgroup
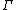as above is called a lattice in N. It is well known that a nilpotent Lie group admits a lattice if and only if its Lie algebra admits a basis with rational structure constants: this is Malcev's criterion. Not all nilpotent Lie group admit lattices; for more details, see also Raghunathan.A compact Riemannian nilmanifold is a compact Riemannian manifold which is locally isometric to a nilpotent Lie group with left-invariant metric. These spaces are constructed as follows. Let
be a lattice in a simply connected nilpotent Lie group N, as above. Endow N with a left-invariant (Riemannian) metric. Then the subgroup 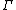acts by isometries on N via left-multiplication. Thus the quotient 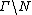is a compact space locally isometric to N. Note: this space is naturally diffeomorphic to 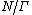.Compact nilmanifolds also arise as principal bundles. For example, consider a 2-step nilpotent Lie group N which admits a lattice (see above). Let
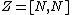be the commutator subgroup of N. Denote by p the dimension of Z and by q the codimension of Z; i.e. the dimension of N is p+q. It is known (see Raghunathan) that 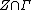is a lattice in Z. Hence, 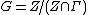is a p-dimensional compact torus. Since Z is central in N, the group G acts on the compact nilmanifold 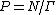with quotient space 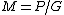. This base manifold M is a q-dimensional compact torus. It has been shown that ever principal torus bundle over a torus is of this form, see . More generally, a compact nilmanifold is torus bundle, over a torus bundle, over...over a torus.As mentioned above, almost flat manifolds are intimately compact nilmanifolds. See that article for more information.
Complex nilmanifolds
Historically, a complex nilmanifold meant a quotient of a complex nilpotent Lie group overa cocompact lattice. An example of such a nilmanifold is an Iwasawa manifold
Iwasawa manifold
In mathematics, in the field of differential geometry, an Iwasawa manifold is a compact quotient of a 3-dimensional complex Heisenberg group by a cocompact, discrete subgroup. AnIwasawa manifold is a nilmanifold, of real dimension 6....
. From the 1980s, another (more general) notion of a complex nilmanifold gradually replaced this one.
An almost complex structure on a real Lie algebra g is an endomorphism
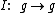which squares to-Idg. This operator is called a complex structure if its eigenspaces, corresponding to eigenvalues
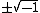, are subalgebras in 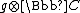. In this case, I defines a left-invariant complex structure on the corresponding Lie group. Such a manifold (G,I) is called a complex group manifold.It is easy to see that every connected complex homogeneous manifold
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
equipped with a free, transitive, holomorphic action by a real Lie group is obtained this way.
Let G be a real, nilpotent Lie group. A complex nilmanifold is a quotient of a complex group manifold (G,I),
equipped with a left-invariant complex structure, by a discrete, cocompact lattice, acting from the right.
Complex nilmanifolds are usually not homogeneous, as complex varieties.
In complex dimension 2, the only complex nilmanifolds are a complex torus and a Kodaira surface
Kodaira surface
In mathematics, a Kodaira surface is a compact complex surface of Kodaira dimension 0 and odd first Betti number.These are never algebraic, though they have non-constant meromorphic functions...
.
Properties
Compact nilmanifolds (except a torus) are never homotopy formal. This implies immediately that compact nilmanifolds (except a torus) cannotadmit a Kähler structure (see also ).
Topologically, all nilmanifolds can be obtained
as iterated torus bundles over a torus. This is easily seen from a filtration by ascending central series.
Nilpotent Lie groups
From the above definition of homogeneous nilmanifolds, it is clear that any nilpotent Lie group with left-invariant metric is a homogeneous nilmanifold. The most familiar nilpotent Lie groups are matrix groups whose diagonal entries are 1 and whose lower diagonal entries are all zeros.For example, the Heisenberg group is a 2-step nilpotent Lie group. This nilpotent Lie group is also special in that it admits a compact quotient. The group
would be the upper triangular matrices with integral coefficients. The resulting nilmanifold is 3-dimensional. One possible fundamental domainFundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
is (isomorphic to) [0,1]3 with the faces identified in a suitable way. This is because an element
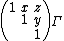of the nilmanifold can be represented by the element 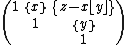in the fundamental domain. Here 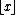denotes the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
of x, and
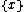the fractional part. The appearance of the floor function here is a clue to the relevance of nilmanifolds to additive combinatorics: the so-called bracket polynomials, or generalised polynomials, seem to be important in the development of higher-order Fourier analysis.Abelian Lie groups
A simpler example would be any abelian Lie group. This is because any such group is a nilpotent Lie group. For example, one can take the group of real numbers under addition, and the discrete, cocompact subgroup consisting of the integers. The resulting 1-step nilmanifold is the familiar circle. Another familiar example might be the compact 2-torus or Euclidean space under addition.Generalizations
A parallel construction based on solvableSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
Lie groups produces a class of spaces called solvmanifolds. An important example of a solvmanifolds are Inoue surface
Inoue surface
In complex geometry, a part of mathematics, the termInoue surface denotes several complex surfacesof Kodaira class VII. They arenamed after Masahisa Inoue, who gave the first non-trivialexamples of Kodaira class VII surfaces in 1974....
s, known in complex geometry
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
.