
Arithmetic combinatorics
Encyclopedia
Arithmetic combinatorics arose out of the interplay between number theory
, combinatorics
, ergodic theory
and harmonic analysis
. It is about combinatorial estimates associated with arithmetic operations (addition, subtraction, multiplication, and division). Additive combinatorics refers to the special case when only the operations of addition and subtraction are involved.
For example: if A is a set of N integers, how large or small can the sumset
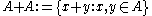 ,
,
the difference set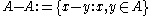 ,
,
and the product set
be, and how are the sizes of these sets related? (Not to be confused: the terms difference set and product set can have other meanings.)
The sets being studied may also belong to other spaces than the integers. e.g. groups
, rings
and fields
.
Arithmetic combinatorics is explained in Green's review of "Additive Combinatorics" by Tao
and Vu
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
. It is about combinatorial estimates associated with arithmetic operations (addition, subtraction, multiplication, and division). Additive combinatorics refers to the special case when only the operations of addition and subtraction are involved.
For example: if A is a set of N integers, how large or small can the sumset
Sumset
In additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
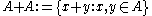 ,
,the difference set
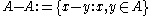 ,
,and the product set

be, and how are the sizes of these sets related? (Not to be confused: the terms difference set and product set can have other meanings.)
The sets being studied may also belong to other spaces than the integers. e.g. groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Arithmetic combinatorics is explained in Green's review of "Additive Combinatorics" by Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
and Vu
Van H. Vu
Van H. Vu is a Vietnamese mathematician, a professor of mathematics at Yale University and the 2008 winner of the Pólya Prize of the Society for Industrial and Applied Mathematics for his work on concentration of measure. He is a collaborator of Terence Tao....
.
See also
- Additive number theoryAdditive number theoryIn number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
- Corners theoremCorners theoremIn mathematics, the corners theorem is an important result, proved by Miklós Ajtai and Endre Szemerédi, of a statement in arithmetic combinatorics...
- Ergodic Ramsey theoryErgodic Ramsey theoryErgodic Ramsey theory is a branch of mathematics where problems motivated by additive combinatorics are proven using ergodic theory.Ergodic Ramsey theory arose shortly after Endre Szemerédi's proof that a set of positive upper density contains arbitrarily long arithmetic progressions, when Hillel...
- Green–Tao theorem
- Problems involving arithmetic progressionsProblems involving arithmetic progressionsProblems involving arithmetic progressions are of interest in number theory, combinatorics, and computer science, both from theoretical and applied points of view.-Largest progression-free subsets:...
- Schnirelmann densitySchnirelmann densityIn additive number theory, the Schnirelmann density of a sequence of numbers is a way to measure how "dense" the sequence is. It is named after Russian mathematician L.G...
- Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
- Sidon set
- Sum-free setSum-free setIn additive combinatorics and number theory, a subset A of an abelian group G is said to be sum-free if the sumset A⊕A is disjoint from A...
- Szemerédi's theoremSzemerédi's theoremIn number theory, Szemerédi's theorem is a result that was formerly the Erdős–Turán conjecture...
Further reading
- Some Highlights of Arithmetic Combinatorics, resources by Terence TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
- Additive Combinatorics: Winter 2007, K Soundararajan
- Earliest Connections of Additive Combinatorics and Computer Science, Luca Trevisan

