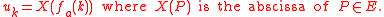Naor-Reingold Pseudorandom Function
Encyclopedia
In 1997, Moni Naor
and Omer Reingold
described efficient constructions for various cryptographic primitive
s in private key as well as public-key cryptography
. Their result is the construction of an efficient pseudorandom function. Let p and l be prime number
s with l |p-1. Select an element g ∈
of multiplicative order
l. Then for each n-dimensional vector
a = (a1, ..., an)∈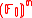
they define the function
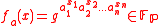
where x = x1 ... xn is the bit representation of integer x, 0 ≤ x ≤ 2n-1, with some extra leading zeros if necessary.
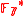of multiplicative order 3 (since 43 = 64 ≡ 1 mod 7). For n = 3, a = (1, 2, 1) and x = 5 (the bit representation of 5 is 101) , we can compute 
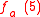as follows:
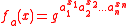
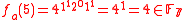
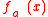in the Naor-Reingold construction can be done very efficiently. Computing the value of the function 
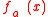at any given point is comparable with one modular exponentiation
and n-modular multiplications. This function can be computed in parallel by threshold circuits of bounded depth and polynomial size.
The Naor-Reingold function can be used as the basis of many cryptographic
schemes including symmetric encryption
, authentication
and digital signatures.
, ... 
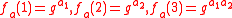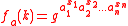and wants to compute 
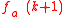. Assume for simplicity that x1 = 0, then the attacker needs to solve the Computational Diffie-Hellman (CDH) between 
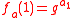and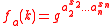 
to get 
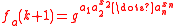. In general, moving from k to k +1 changes the bit pattern and unless k + 1 is a power of 2 one can split the exponent in 
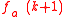so that the computation corresponds to computing the Diffie-Hellman
key between two of the earlier results. This attacker wants to predict the next sequence
element. Such an attack would be very bad—but it's also possible to fight it off by working in groups
with a hard Diffie-Hellman problem
(DHP).
Example:
An attacker sees several outputs of the function e.g.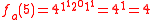
, as in the previous example, and 
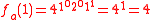. Then, the attacker wants to predict the next sequence element of this function, 
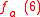. However, the attacker cannot predict the outcome of 
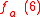from knowing 
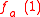and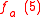 
.
There are other attacks that would be very bad for a Pseudorandom Number Generator
: the user expects to get random numbers from the output, so of course the stream should not be predictable, but even more, it should be indistinguishable from a random string. Let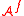
denote the algorithm 
with access to an oracle for evaluating the function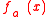 
. Suppose the Decisional Diffie-Hellman assumption
holds for
, Naor and Reingold show that for every probabilistic polynomial time
algorithm
and sufficiently large n
The first probability is taken over the choice of the seed s = (p, g, a) and the second probability is taken over the random distribution induced on p, g by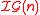
, instance generator, and the random choice of the function 
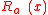among the set of all 
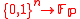functions.
purposes is the size of its linear complexity. The linear complexity of an n-element sequence W(x), x = 0,1,2,…,n – 1, over a ring
is the length l of the shortest linear recurrence relation
W (x + l) = Al-1 W (x +l-1) + … + A0 W(x), x = 0,1,2,…, n – l –1 with A0, …, Al-1 ∈
, which is satisfied by this sequence.
For some
> 0,n ≥ (1+ 
) 
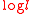, for any 
, sufficiently large l, the linear complexity of the sequence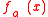 
,0 ≤ x ≤ 2n-1, denoted by 
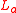satisfies
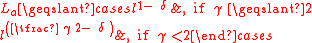
for all except possibly at most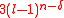
vectors a ∈ 
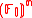. The bound of this work has disadvantages, namely it does not apply to the very interesting case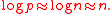 
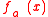is exponentially close to uniform distribution for almost all vectors a ∈ 
.
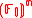Let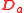
be the discrepancy
of the set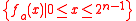
. Thus, if 
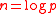is the bit length of p then for all vectors a ∈ 
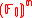the bound 
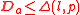holds, where
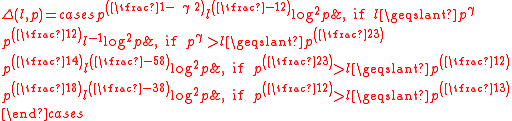
and
= 2.5 -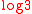 
= 0.9150....
Although this property does not seem to have any immediate cryptographic implications, the inverse fact, namely non uniform distribution, if true would have disastrous consequences for applications of this function.
version of this function is of interest as well. In particular, it may help to improve the cryptographic security of the corresponding system. Let p > 3 be prime and let E be an elliptic curve over
, then each vector a defines a finite sequence in the subgroup
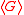as: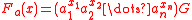
where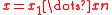
is the bit representation of integer 
.
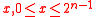The Naor-Reingold elliptic curve sequence is defined as
If the Decisional Diffie-Hellman assumption holds, the index k is not enough to compute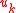
in polynomial time, even if an attacker performs polynomially many queries to a random oracle.
Moni Naor
Moni Naor is an Israeli computer scientist, currently a professor at the Weizmann Institute of Science. Naor received his Ph.D. in 1989 at the University of California, Berkeley. His adviser was Manuel Blum....
and Omer Reingold
Omer Reingold
Omer Reingold is a faculty member of the Foundations of Computer Science Group at the Weizmann Institute of Science, Israel. He received the 2005 Grace Murray Hopper Award for his work in finding a deterministic logarithmic-space algorithm for ST-connectivity in undirected graphs...
described efficient constructions for various cryptographic primitive
Cryptographic primitive
Cryptographic primitives are well-established, low-level cryptographic algorithms that are frequently used to build computer security systems. These routines include, but are not limited to, one-way hash functions and encryption functions.- Rationale :...
s in private key as well as public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
. Their result is the construction of an efficient pseudorandom function. Let p and l be prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s with l |p-1. Select an element g ∈
of multiplicative orderMultiplicative order
In number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
l. Then for each n-dimensional vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
a = (a1, ..., an)∈
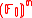they define the function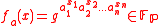where x = x1 ... xn is the bit representation of integer x, 0 ≤ x ≤ 2n-1, with some extra leading zeros if necessary.
Example
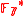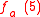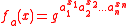
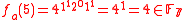
Let p = 7, p – 1 = 6, and l = 3, l |p-1. Select g = 4 ∈ of multiplicative order 3 (since 43 = 64 ≡ 1 mod 7). For n = 3, a = (1, 2, 1) and x = 5 (the bit representation of 5 is 101) , we can compute as follows:Efficiency
The evaluation of function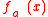 in the Naor-Reingold construction can be done very efficiently. Computing the value of the function 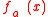at any given point is comparable with one modular exponentiationModular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
and n-modular multiplications. This function can be computed in parallel by threshold circuits of bounded depth and polynomial size.
The Naor-Reingold function can be used as the basis of many cryptographic
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
schemes including symmetric encryption
Symmetric-key algorithm
Symmetric-key algorithms are a class of algorithms for cryptography that use trivially related, often identical, cryptographic keys for both encryption of plaintext and decryption of ciphertext. The encryption key is trivially related to the decryption key, in that they may be identical or there is...
, authentication
Authentication
Authentication is the act of confirming the truth of an attribute of a datum or entity...
and digital signatures.
Security of the Function
Assume that an attacker sees several outputs of the function, e.g.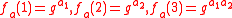, ... 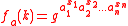and wants to compute 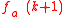. Assume for simplicity that x1 = 0, then the attacker needs to solve the Computational Diffie-Hellman (CDH) between 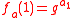and 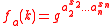to get 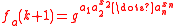. In general, moving from k to k +1 changes the bit pattern and unless k + 1 is a power of 2 one can split the exponent in 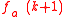so that the computation corresponds to computing the Diffie-HellmanDiffie-Hellman problem
The Diffie–Hellman problem is a mathematical problem first proposed by Whitfield Diffie and Martin Hellman in the context of cryptography. The motivation for this problem is that many security systems use mathematical operations that are fast to compute, but hard to reverse. For example, they...
key between two of the earlier results. This attacker wants to predict the next sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
element. Such an attack would be very bad—but it's also possible to fight it off by working in groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with a hard Diffie-Hellman problem
Diffie-Hellman problem
The Diffie–Hellman problem is a mathematical problem first proposed by Whitfield Diffie and Martin Hellman in the context of cryptography. The motivation for this problem is that many security systems use mathematical operations that are fast to compute, but hard to reverse. For example, they...
(DHP).
Example:
An attacker sees several outputs of the function e.g.
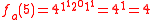, as in the previous example, and 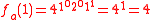. Then, the attacker wants to predict the next sequence element of this function, 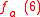. However, the attacker cannot predict the outcome of 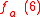from knowing 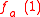and 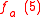.There are other attacks that would be very bad for a Pseudorandom Number Generator
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
: the user expects to get random numbers from the output, so of course the stream should not be predictable, but even more, it should be indistinguishable from a random string. Let
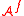denote the algorithm with access to an oracle for evaluating the function 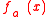. Suppose the Decisional Diffie-Hellman assumptionDecisional Diffie-Hellman assumption
The decisional Diffie–Hellman assumption is a computational hardness assumption about a certain problem involving discrete logarithms in cyclic groups. It is used as the basis to prove the security of many cryptographic protocols, most notably the ElGamal and Cramer–Shoup...
holds for
, Naor and Reingold show that for every probabilistic polynomial timePP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
algorithm
and sufficiently large n-
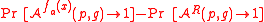is negligible.
The first probability is taken over the choice of the seed s = (p, g, a) and the second probability is taken over the random distribution induced on p, g by
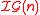, instance generator, and the random choice of the function 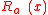among the set of all 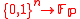functions.Linear Complexity
One natural measure of how useful a sequence may be for cryptographicCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
purposes is the size of its linear complexity. The linear complexity of an n-element sequence W(x), x = 0,1,2,…,n – 1, over a ring
is the length l of the shortest linear recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
W (x + l) = Al-1 W (x +l-1) + … + A0 W(x), x = 0,1,2,…, n – l –1 with A0, …, Al-1 ∈
, which is satisfied by this sequence.For some
> 0,n ≥ (1+ ) 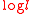, for any , sufficiently large l, the linear complexity of the sequence 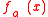,0 ≤ x ≤ 2n-1, denoted by 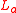satisfies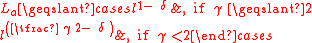for all except possibly at most
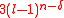vectors a ∈ 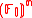. The bound of this work has disadvantages, namely it does not apply to the very interesting case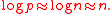 Uniformity of Distribution
The statistical distribution of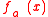 is exponentially close to uniform distribution for almost all vectors a ∈ 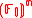.Let
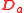be the discrepancyInversive congruential generator
Inversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence...
of the set
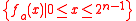. Thus, if 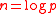is the bit length of p then for all vectors a ∈ 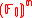the bound 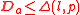holds, where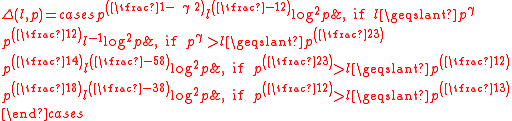and
= 2.5 - 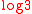= 0.9150....Although this property does not seem to have any immediate cryptographic implications, the inverse fact, namely non uniform distribution, if true would have disastrous consequences for applications of this function.
Sequences in Elliptic Curve
The elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
version of this function is of interest as well. In particular, it may help to improve the cryptographic security of the corresponding system. Let p > 3 be prime and let E be an elliptic curve over
, then each vector a defines a finite sequence in the subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
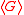as: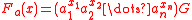where
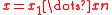is the bit representation of integer 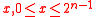.The Naor-Reingold elliptic curve sequence is defined as
If the Decisional Diffie-Hellman assumption holds, the index k is not enough to compute
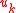in polynomial time, even if an attacker performs polynomially many queries to a random oracle.See also
- Decisional Diffie-Hellman assumptionDecisional Diffie-Hellman assumptionThe decisional Diffie–Hellman assumption is a computational hardness assumption about a certain problem involving discrete logarithms in cyclic groups. It is used as the basis to prove the security of many cryptographic protocols, most notably the ElGamal and Cramer–Shoup...
- Finite FieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
- Inversive congruential generatorInversive congruential generatorInversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence...
- Generalized inversive congruential pseudorandom numbersGeneralized inversive congruential pseudorandom numbersAn approach to nonlinear congruential methods of generating uniform pseudorandom numbers in the interval [0,1) is the Inversive congruential generator with prime modulus...