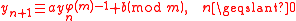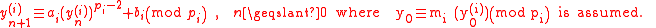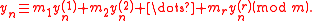Generalized inversive congruential pseudorandom numbers
Encyclopedia
An approach to nonlinear congruential methods of generating uniform pseudorandom numbers
in the interval [0,1) is the Inversive congruential generator
with prime modulus. A generalization for arbitrary composite moduli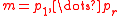 with arbitrary distinct primes
with arbitrary distinct primes
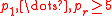 will be present here.
will be present here.
Let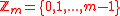 .For integer
.For integer
s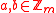 with gcd (a,m) = 1 a generalized inversive congruential sequence
with gcd (a,m) = 1 a generalized inversive congruential sequence 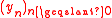 of elements of
of elements of 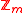 is defined by
is defined by
where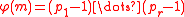 denotes the number of positive integers less than m which are relatively prime
denotes the number of positive integers less than m which are relatively prime
to m.
 and
and 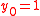 . Hence
. Hence 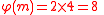 and the sequence
and the sequence 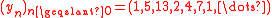 is not maximum.
is not maximum.
The result below shows that these sequences are closely related to the following inversive congruential sequence with prime moduli.
For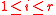 let
let 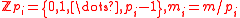 and
and 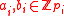 be integers with
be integers with
Let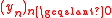 be a sequence of elements of
be a sequence of elements of 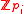 , given by
, given by
 for
for 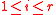 be defined as above.
be defined as above.
Then
This theorem shows that an implementation of Generalized Inversive Congruential Generator is possible,where exact integer computations have to be performed only in but not in
but not in 
Proof:
First, observe that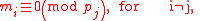 and hence
and hence 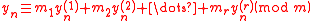 if and only if
if and only if 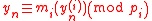 , for
, for 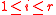 which will be shown on induction on
which will be shown on induction on 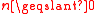 .
.
Recall that is assumed for
is assumed for 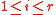 . Now, suppose that
. Now, suppose that 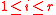 and
and 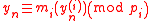 for some integer
for some integer 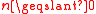 . Then straightforward calculations and Fermat's Theorem
. Then straightforward calculations and Fermat's Theorem
yield
which implies the desired result.
Generalized Inversive Congruential Pseudorandom Numbers are well equidistributed in one dimension. A reliable theoretical approach for assessing their statistical independence properties is based on the discrepancy of s-tuples of pseudorandom numbers.
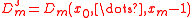 where
where 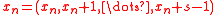
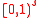 of Generalized Inversive Congruential Pseudorandom Numbers for
of Generalized Inversive Congruential Pseudorandom Numbers for  .
.
Higher bound
Lower bound:
For a fixed number r of prime factors of m, Theorem 2 shows that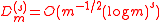
for any Generalized Inversive Congruential Sequence. In this case Theorem 3 implies that there exist Generalized Inversive Congruential Generators having a discrepancy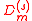 which is at least of the order of magnitude
which is at least of the order of magnitude 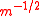 for all dimension
for all dimension  . However,if m is composed only of small primes, then r can be of an order of magnitude
. However,if m is composed only of small primes, then r can be of an order of magnitude 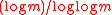 and hence
and hence 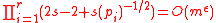 for every
for every  . Therefore, one obtains in the general case
. Therefore, one obtains in the general case 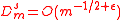 for every
for every  .
.
Since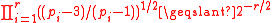 , similar arguments imply that in the general case the lower bound in Theorem 3 is at least of the order of magnitude
, similar arguments imply that in the general case the lower bound in Theorem 3 is at least of the order of magnitude
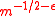 for every
for every  . It is this range of magnitudes where one also finds the discrepancy of m independent and uniformly distributed random points which almost always has the order of magnitude
. It is this range of magnitudes where one also finds the discrepancy of m independent and uniformly distributed random points which almost always has the order of magnitude
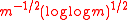
according to the law of the iterated logarithm for discrepancies. In this sense, Generalized Inversive Congruential Pseudo-random Numbers model true random numbers very closely.
Pseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
in the interval [0,1) is the Inversive congruential generator
Inversive congruential generator
Inversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence...
with prime modulus. A generalization for arbitrary composite moduli
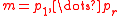 with arbitrary distinct primes
with arbitrary distinct primesPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
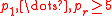 will be present here.
will be present here.Let
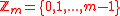 .For integer
.For integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s
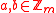 with gcd (a,m) = 1 a generalized inversive congruential sequence
with gcd (a,m) = 1 a generalized inversive congruential sequence 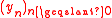 of elements of
of elements of 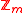 is defined by
is defined bywhere
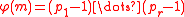 denotes the number of positive integers less than m which are relatively prime
denotes the number of positive integers less than m which are relatively primeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to m.
Example
Let take m = 15 = and
and 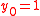 . Hence
. Hence 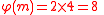 and the sequence
and the sequence 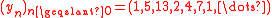 is not maximum.
is not maximum.The result below shows that these sequences are closely related to the following inversive congruential sequence with prime moduli.
For
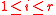 let
let 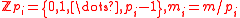 and
and 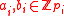 be integers with
be integers withLet
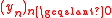 be a sequence of elements of
be a sequence of elements of 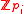 , given by
, given byTheorem 1
Let for
for 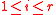 be defined as above.
be defined as above.Then
This theorem shows that an implementation of Generalized Inversive Congruential Generator is possible,where exact integer computations have to be performed only in
 but not in
but not in 
Proof:
First, observe that
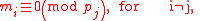 and hence
and hence 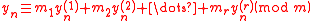 if and only if
if and only if 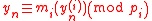 , for
, for 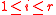 which will be shown on induction on
which will be shown on induction on 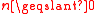 .
.Recall that
 is assumed for
is assumed for 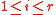 . Now, suppose that
. Now, suppose that 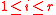 and
and 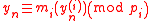 for some integer
for some integer 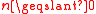 . Then straightforward calculations and Fermat's Theorem
. Then straightforward calculations and Fermat's TheoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
yield
-
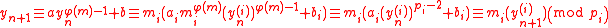 ,
,
which implies the desired result.
Generalized Inversive Congruential Pseudorandom Numbers are well equidistributed in one dimension. A reliable theoretical approach for assessing their statistical independence properties is based on the discrepancy of s-tuples of pseudorandom numbers.
Discrepancy bounds of the GIC Generator
We use the notation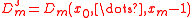 where
where 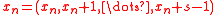
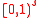 of Generalized Inversive Congruential Pseudorandom Numbers for
of Generalized Inversive Congruential Pseudorandom Numbers for  .
.Higher bound
- Let

- Then the discrepancy
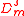 satisfies
satisfies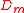
 <
< 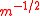
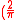
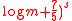
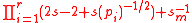 for any Generalized Inversive Congruential operator.
for any Generalized Inversive Congruential operator.
Lower bound:
- There exist Generalized Inversive Congruential Generators with
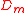

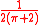
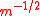 :
: 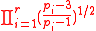 for all dimension s 2.
for all dimension s 2.
For a fixed number r of prime factors of m, Theorem 2 shows that
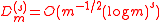
for any Generalized Inversive Congruential Sequence. In this case Theorem 3 implies that there exist Generalized Inversive Congruential Generators having a discrepancy
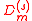 which is at least of the order of magnitude
which is at least of the order of magnitude 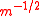 for all dimension
for all dimension  . However,if m is composed only of small primes, then r can be of an order of magnitude
. However,if m is composed only of small primes, then r can be of an order of magnitude 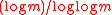 and hence
and hence 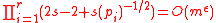 for every
for every  . Therefore, one obtains in the general case
. Therefore, one obtains in the general case 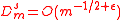 for every
for every  .
.Since
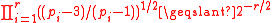 , similar arguments imply that in the general case the lower bound in Theorem 3 is at least of the order of magnitude
, similar arguments imply that in the general case the lower bound in Theorem 3 is at least of the order of magnitude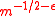 for every
for every  . It is this range of magnitudes where one also finds the discrepancy of m independent and uniformly distributed random points which almost always has the order of magnitude
. It is this range of magnitudes where one also finds the discrepancy of m independent and uniformly distributed random points which almost always has the order of magnitude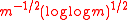
according to the law of the iterated logarithm for discrepancies. In this sense, Generalized Inversive Congruential Pseudo-random Numbers model true random numbers very closely.
See also
- Pseudorandom number generatorPseudorandom number generatorA pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
- List of random number generators
- Linear congruential generatorLinear congruential generatorA Linear Congruential Generator represents one of the oldest and best-known pseudorandom number generator algorithms. The theory behind them is easy to understand, and they are easily implemented and fast....
- Inversive congruential generatorInversive congruential generatorInversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence...
- Naor-Reingold Pseudorandom Function