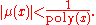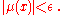Negligible function
Encyclopedia
In mathematics, a negligible function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
 such that for every positive integer c there exists an integer Nc such that for all x > Nc,
such that for every positive integer c there exists an integer Nc such that for all x > Nc,
Equivalently, we may also use the following definition.
A function
 is negligible, if for every positive polynomial
is negligible, if for every positive polynomialPositive polynomial
In mathematics, a positive polynomial on a particular set is a polynomial whose values are positive on that set.Let p be a polynomial in n variables with real coefficients and let S be a subset of the n-dimensional Euclidean space ℝn...
poly(·) there exists an integer Npoly > 0 such that for all x > Npoly
History
The concept of negligibility can find its trace back to sound models of analysis. Though the concepts of "continuityContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
" and "infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
" became important in mathematics during Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
's time (1680s), they were not well-defined until late 1810s. The first reasonably rigorous definition of continuity in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
was due to Bernard Bolzano
Bernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
, who wrote in 1817 the modern definition of continuity. Lately Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
, Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
and Heine
Eduard Heine
Heinrich Eduard Heine was a German mathematician.Heine became known for results on special functions and in real analysis. In particular, he authored an important treatise on spherical harmonics and Legendre functions . He also investigated basic hypergeometric series...
also defined as follows (with all numbers in the real number domain
 ):
):- (Continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
) A function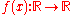 is continuous at
is continuous at 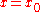 if for every
if for every  , there exists a positive number
, there exists a positive number  such that
such that  implies
implies 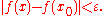
This classic definition of continuity can be transformed into the
definition of negligibility in a few steps by changing a parameter used in the definition per step. First, in case
 with
with 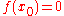 , we must define the concept of "infinitesimal function":
, we must define the concept of "infinitesimal function":- (InfinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
) A continuous function is infinitesimal (as
is infinitesimal (as  goes to infinity) if for every
goes to infinity) if for every  there exists
there exists 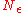 such that for all
such that for all 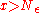
Next, we replace
 by the functions
by the functions 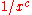 where
where  or by
or by 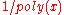 where
where 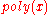 is a positive polynomial. This leads to the definitions of negligible functions given at the top of this article. Since the constants
is a positive polynomial. This leads to the definitions of negligible functions given at the top of this article. Since the constants  can be expressed as
can be expressed as 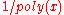 with a constant polynomial this shows that negligible functions are a subset of the infinitesimal functions.
with a constant polynomial this shows that negligible functions are a subset of the infinitesimal functions.In complexity-based modern cryptography, a security scheme is
provably secure
Provable security
In cryptography, a system has provable security if its security requirements can be stated formally in an adversarial model, as opposed to heuristically, with clear assumptions that the adversary has access to the system as well as enough computational resources...
if the probability of security failure (e.g.,
inverting a one-way function
One-way function
In computer science, a one-way function is a function that is easy to compute on every input, but hard to invert given the image of a random input. Here "easy" and "hard" are to be understood in the sense of computational complexity theory, specifically the theory of polynomial time problems...
, distinguishing cryptographically strong pseudorandom bits
Cryptographically secure pseudorandom number generator
A cryptographically secure pseudo-random number generator is a pseudo-random number generator with properties that make it suitable for use in cryptography.Many aspects of cryptography require random numbers, for example:...
from truly random bits) is negligible in terms of the input
 = cryptographic key length
= cryptographic key length  . Hence comes the definition at the top of the page because key length
. Hence comes the definition at the top of the page because key length  must be a natural number.
must be a natural number.Nevertheless, the general notion of negligibility has never said that the system input parameter
 must be the key length
must be the key length  . Indeed,
. Indeed,  can be any predetermined system metric and corresponding mathematic analysis would illustrate some hidden analytical behaviors of the system.
can be any predetermined system metric and corresponding mathematic analysis would illustrate some hidden analytical behaviors of the system.The reciprocal-of-polynomial formulation is used for the same reason that computational boundedness is defined as polynomial running time: it has mathematical closure properties that make it tractable in the asymptotic setting. For example, if an attack succeeds in violating a security condition only with negligible probability, and the attack is repeated a polynomial number of times, the success probability of the overall attack still remains negligible.
In practice one might want to have more concrete
Concrete security
In cryptography, concrete security or exact security is a practice-oriented approach that aims to give more precise estimates of the computational complexities of adversarial tasks than polynomial equivalence would allow....
functions bounding the adversary's success probability and to choose the security parameter large enough that this probability is smaller than some threshold, say 2−128.
See also
- Negligible setNegligible setIn mathematics, a negligible set is a set that is small enough that it can be ignored for some purpose.As common examples, finite sets can be ignored when studying the limit of a sequence, and null sets can be ignored when studying the integral of a measurable function.Negligible sets define...
- Colombeau algebraColombeau algebraIn mathematics, the Colombeau algebra is an algebra introduced with the aim of constructing an improved theory of distributions in which multiplication is not problematic...
- Nonstandard numbersNon-standard analysisNon-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
- Gromov's theorem on groups of polynomial growthGromov's theorem on groups of polynomial growthIn geometric group theory, Gromov's theorem on groups of polynomial growth, named for Mikhail Gromov, characterizes finitely generated groups of polynomial growth, as those groups which have nilpotent subgroups of finite index....
- Non-standard calculusNon-standard calculusIn mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...