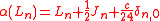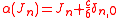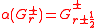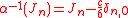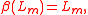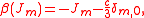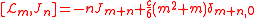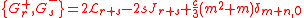N = 2 superconformal algebra
Encyclopedia
In mathematical physics
, the N = 2 superconformal algebra is an infinite-dimensional Lie superalgebra
, related to supersymmetry
, that occurs in string theory
and conformal field theory
. It has important applications in mirror symmetry
. It was introduced by as a gauge algebra of the U(1) fermionic string.
The N = 2 superconformal algebra is the Lie superalgebra with basis of even elements c, Ln, Jn, for n an integer, and odd elements G, G, where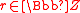
(for the Ramond basis) or 
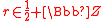(for the Neveu–Schwarz basis) defined by the following relations:
If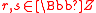
in these relations, this yields the
N = 2 Ramond algebra; while if
are
half-integers, it gives the N = 2 Neveu–Schwarz algebra. The operators
generate a Lie subalgebra isomorphic to the Virasoro algebra
. Together with the operators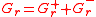
, they generate a Lie superalgebra isomorphic to the super Virasoro algebra,
giving the Ramond algebra if
are integers and the Neveu–Schwarz algebra otherwise. When represented as operators on a complex inner product space
,
is taken to act as multiplication by a real scalar, denoted by the same letter and called the central charge, and the adjoint structure is as follows:
s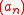
, 
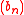
and a complex fermionic field
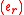
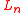is defined to the sum of the Virasoro operators naturally associated with each of the three systems
where normal ordering has been used for bosons and fermions.
The current operator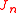
is defined by the standard construction from fermions
and the two supersymmetric operators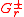
by
This yields an N = 2 Neveu–Schwarz algebra with c = 3.
s of for the discrete series representations of the Virasoro and super Virasoro algebra. Given a representation of the affine Kac-Moody algebra of SU(2) at level
with basis 
satisfying
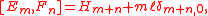
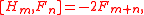
the supersymmetric generators are defined by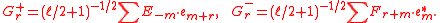
This yields the N=2 superconformal algebra with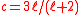
.
The algebra commutes with the bosonic operators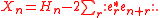
The space of physical states consists of eigenvectors of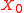
simultaneously annihilated by the 
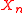's for positive 
and the supercharge operator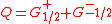
(Neveu–Schwarz)
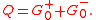(Ramond)
The supercharge operator commutes with the action of the affine Weyl group and the physical states lie in a single orbit of this group, a fact which implies the Weyl-Kac character formula.
and a closed subgroup 
of maximal rank, i.e. containing a maximal torus
of 
, with the additional condition that
the dimension of the centre of
is non-zero. In this case the compact Hermitian symmetric space
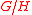is a Kähler manifold, for example when 
. The physical states lie in a single orbit of the affine Weyl group, which again implies the Weyl–Kac character formula for the affine Kac–Moody algebra of 
.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the N = 2 superconformal algebra is an infinite-dimensional Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
, related to supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, that occurs in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
and conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
. It has important applications in mirror symmetry
Mirror symmetry
In physics and mathematics, mirror symmetry is a relation that can exist between two Calabi-Yau manifolds. It happens, usually for two such six-dimensional manifolds, that the shapes may look very different geometrically, but nevertheless they are equivalent if they are employed as hidden...
. It was introduced by as a gauge algebra of the U(1) fermionic string.
Definition
There are two slightly different ways to describe the N = 2 superconformal algebra, called the N = 2 Ramond algebra and the N = 2 Neveu–Schwarz algebra, which are isomorphic (see below) but differ in the choice of standard basis.The N = 2 superconformal algebra is the Lie superalgebra with basis of even elements c, Ln, Jn, for n an integer, and odd elements G, G, where
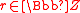(for the Ramond basis) or 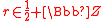(for the Neveu–Schwarz basis) defined by the following relations:-
- c is in the center
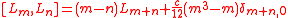
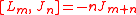
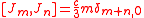
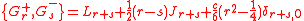
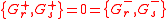
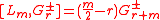
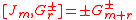
If
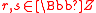in these relations, this yields theN = 2 Ramond algebra; while if
arehalf-integers, it gives the N = 2 Neveu–Schwarz algebra. The operators
generate a Lie subalgebra isomorphic to the Virasoro algebraVirasoro algebra
In mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
. Together with the operators
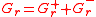, they generate a Lie superalgebra isomorphic to the super Virasoro algebra,giving the Ramond algebra if
are integers and the Neveu–Schwarz algebra otherwise. When represented as operators on a complex inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
,
is taken to act as multiplication by a real scalar, denoted by the same letter and called the central charge, and the adjoint structure is as follows:Properties
- The N = 2 Ramond and Neveu–Schwarz algebras are isomorphic by the spectral shift isomorphism
of :
- with inverse:
- In the N = 2 Ramond algebra, the zero mode operators
, 
, 
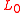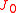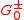and the constants form a five-dimensional Lie superalgebra. They satisfy the same relations as the fundamental operators in Kähler geometryKähler manifoldIn mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
, with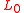
corresponding to the Laplacian, 
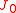the degree operator, and 
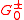the 
and 
operators.
- Even integer powers of the spectral shift give automorphisms of the N = 2 superconformal algebras, called spectral shift automorphisms. Another automorphism
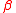, of period two, is given by
- In terms of Kähler operators,
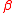corresponds to conjugating the complex structure. Since 
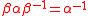, the automorphisms 
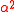and 
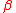generate a group of automorphisms of the N = 2 superconformal algebra isomorphic to the infinite dihedral groupInfinite dihedral groupIn mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.-Definition:...
.
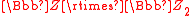- Twisted operators
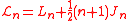were introduced by and satisfy:
- so that these operators satisfy the Virasoro relation with central charge 0. The constant
still appears in the relations for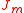 
and the modified relations
Free field construction
give a construction using two commuting real bosonic fieldBosonic field
In quantum field theory, a bosonic field is a quantum field whose quanta are bosons; that is, they obey Bose-Einstein statistics. Bosonic fields obey canonical commutation relations, as distinct from the canonical anticommutation relations obeyed by fermionic fields.Examples include scalar fields,...
s
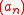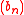
, and a complex fermionic field
Fermionic field
In quantum field theory, a fermionic field is a quantum field whose quanta are fermions; that is, they obey Fermi-Dirac statistics. Fermionic fields obey canonical anticommutation relations rather than the canonical commutation relations of bosonic fields....
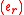
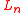is defined to the sum of the Virasoro operators naturally associated with each of the three systemswhere normal ordering has been used for bosons and fermions.
The current operator
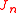is defined by the standard construction from fermionsand the two supersymmetric operators
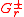byThis yields an N = 2 Neveu–Schwarz algebra with c = 3.
SU(2) supersymmetric coset construction
gave a coset construction of the N = 2 superconformal algebras, generalizing the coset constructionCoset construction
In mathematics, the coset construction is a method of constructing unitary highest weight representations of the Virasoro algebra, introduced by Peter Goddard, Adrian Kent and David Olive...
s of for the discrete series representations of the Virasoro and super Virasoro algebra. Given a representation of the affine Kac-Moody algebra of SU(2) at level
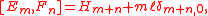
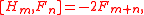
with basis satisfyingthe supersymmetric generators are defined by
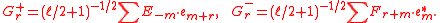
This yields the N=2 superconformal algebra with
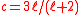.The algebra commutes with the bosonic operators
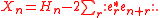
The space of physical states consists of eigenvectors of
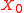simultaneously annihilated by the 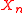's for positive and the supercharge operator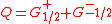 (Neveu–Schwarz) 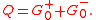(Ramond)The supercharge operator commutes with the action of the affine Weyl group and the physical states lie in a single orbit of this group, a fact which implies the Weyl-Kac character formula.
Kazama–Suzuki supersymmetric coset construction
generalized the SU(2) coset construction to any pair consisting of a simple compact Lie group and a closed subgroup of maximal rank, i.e. containing a maximal torusMaximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
of , with the additional condition thatthe dimension of the centre of
is non-zero. In this case the compact Hermitian symmetric spaceHermitian symmetric space
In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian...
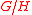is a Kähler manifold, for example when . The physical states lie in a single orbit of the affine Weyl group, which again implies the Weyl–Kac character formula for the affine Kac–Moody algebra of .See also
- Virasoro algebraVirasoro algebraIn mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
- Super Virasoro algebra
- Coset constructionCoset constructionIn mathematics, the coset construction is a method of constructing unitary highest weight representations of the Virasoro algebra, introduced by Peter Goddard, Adrian Kent and David Olive...
- Type IIB string theory