
Ménage problem
Encyclopedia
In combinatorial
mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of heterosexual couples at a dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas
and independently, a few years earlier, by Peter Guthrie Tait
in connection with knot theory
. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is
Mathematicians have developed formulas and recurrence equations for computing these numbers and related sequences of numbers. Along with their applications to etiquette and knot theory, these numbers also have a graph theoretic
interpretation: they count the numbers of matchings and Hamiltonian cycles in certain families of graphs.
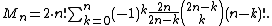
Much subsequent work has gone into alternative proofs for this formula and into generalized versions of the problem that count seating arrangements in which some couples are permitted to sit next to each other. A different formula for Mn involving Chebyshev polynomials was given by .
There are 2×n! ways of seating the women, as there are two choices for which set of seats to place the women into and n! choices for how to place them into that set of seats. For each seating arrangement for the women, there are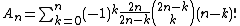
ways of seating the men; this formula simply omits the 2×n! factor from Touchard's formula. The resulting sequence of smaller numbers (again, starting from n = 3),
is called the sequence of ménage numbers. They satisfy the recurrence relation
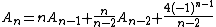
and the simpler four-term recurrence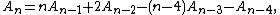
from which the ménage numbers themselves may easily be calculated.
terms, as directed
Hamiltonian cycles of crown graph
s. A crown graph is formed by removing a perfect matching from a complete bipartite graph
Kn,n; it has 2n vertices of two colors, and each vertex of one color is connected to all but one of the vertices of the other color. In the case of the ménage problem, the vertices of the graph represent men and women, and the edges represent pairs of men and women who are allowed to sit next to each other. This graph is formed by removing the perfect matching formed by the heterosexual couples from a complete bipartite graph that connects every man to every woman. Any valid seating arrangement can be described by the sequence of people in order around the table, which forms a Hamiltonian cycle in the graph. However, two Hamiltonian cycles are considered to be equivalent if they connect the same vertices in the same cyclic order regardless of the starting vertex, while in the ménage problem the starting position is considered significant: if, as in Alice
's tea party, all the guests shift their positions by one seat, it is considered a different seating arrangement even though it is described by the same cycle. Therefore, the number of oriented Hamiltonian cycles in a crown graph is smaller by a factor of 2n than the number of seating arrangements, but larger by a factor of (n − 1)! than the ménage numbers. The sequence of numbers of cycles in these graphs (as before, starting at n = 3) is
A second graph-theoretic description of the problem is also possible. Once the women have been seated, the possible seating arrangements for the remaining men can be described as perfect matchings in a graph formed by removing a single Hamiltonian cycle from a complete bipartite graph; the graph has edges connecting open seats to men, and the removal of the cycle corresponds to forbidding the men to sit in either of the open seats adjacent to their wives. The problem of counting matchings in a bipartite graph, and therefore a fortiori the problem of computing ménage numbers, can be solved using the permanent
s of certain 0-1 matrices
. In the case of the ménage problem, the matrices arising from this view of the problem are circulant matrices
.
s with a given number of crossings
. In Dowker notation
for knot diagrams, an early form of which was used by Tait, the 2n points where a knot with n knots crosses itself, in consecutive order along the knot, are labeled with the 2n numbers from 1 to 2n. In a reduced diagram, the two labels at a crossing cannot be consecutive, so the set of pairs of labels at each crossing, used in Dowker notation to represent the knot, can be interpreted as a perfect matching in a graph that has a vertex for every number in the range from 1 to 2n and an edge between every pair of numbers that has different parity and are non-consecutive modulo 2n. This graph is formed by removing a Hamiltonian cycle (connecting consecutive numbers) from a complete bipartite graph (connecting all pairs of numbers with different parity), and so it has a number of matchings equal to a ménage number. For alternating knot
s, this matching is enough to describe the knot diagram itself; for other knots, an additional positive or negative sign needs to be specified for each crossing pair to determine which of the two strands of the crossing lies above the other strand.
However, the knot listing problem has some additional symmetries not present in the ménage problem: one obtains different Dowker notations for the same knot diagram if one begins the labeling at a different crossing point, and these different notations should all be counted as representing the same diagram. For this reason, two matchings that differ from each other by a cyclic permutation
should be treated as equivalent and counted only once. solved this modified enumeration problem, showing that the number of different matchings is
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of heterosexual couples at a dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
and independently, a few years earlier, by Peter Guthrie Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
in connection with knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is
- 12, 96, 3120, 115200, 5836320, 382072320, 31488549120, ... .
Mathematicians have developed formulas and recurrence equations for computing these numbers and related sequences of numbers. Along with their applications to etiquette and knot theory, these numbers also have a graph theoretic
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
interpretation: they count the numbers of matchings and Hamiltonian cycles in certain families of graphs.
Touchard's formula
Let Mn denote the number of seating arrangements for n couples. derived the formula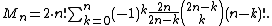
Much subsequent work has gone into alternative proofs for this formula and into generalized versions of the problem that count seating arrangements in which some couples are permitted to sit next to each other. A different formula for Mn involving Chebyshev polynomials was given by .
Ménage numbers and ladies-first solutions
Until the work of , solutions to the ménage problem took the form of first finding all seating arrangements for the women and then counting, for each of these partial seating arrangements, the number of ways of completing it by seating the men away from their wives. However, as Bogart and Doyle showed, Touchard's formula may be more directly derived by considering all seating arrangements at once rather than by factoring out the participation of the women.There are 2×n! ways of seating the women, as there are two choices for which set of seats to place the women into and n! choices for how to place them into that set of seats. For each seating arrangement for the women, there are
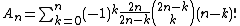
ways of seating the men; this formula simply omits the 2×n! factor from Touchard's formula. The resulting sequence of smaller numbers (again, starting from n = 3),
- 1, 2, 13, 80, 579, 4738, 43387, 439792, ...
is called the sequence of ménage numbers. They satisfy the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
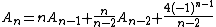
and the simpler four-term recurrence
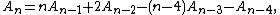
from which the ménage numbers themselves may easily be calculated.
Graph-theoretical interpretation
Solutions to the ménage problem may be interpreted in graph-theoreticGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
terms, as directed
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
Hamiltonian cycles of crown graph
Crown graph
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j...
s. A crown graph is formed by removing a perfect matching from a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Kn,n; it has 2n vertices of two colors, and each vertex of one color is connected to all but one of the vertices of the other color. In the case of the ménage problem, the vertices of the graph represent men and women, and the edges represent pairs of men and women who are allowed to sit next to each other. This graph is formed by removing the perfect matching formed by the heterosexual couples from a complete bipartite graph that connects every man to every woman. Any valid seating arrangement can be described by the sequence of people in order around the table, which forms a Hamiltonian cycle in the graph. However, two Hamiltonian cycles are considered to be equivalent if they connect the same vertices in the same cyclic order regardless of the starting vertex, while in the ménage problem the starting position is considered significant: if, as in Alice
Alice's Adventures in Wonderland
Alice's Adventures in Wonderland is an 1865 novel written by English author Charles Lutwidge Dodgson under the pseudonym Lewis Carroll. It tells of a girl named Alice who falls down a rabbit hole into a fantasy world populated by peculiar, anthropomorphic creatures...
's tea party, all the guests shift their positions by one seat, it is considered a different seating arrangement even though it is described by the same cycle. Therefore, the number of oriented Hamiltonian cycles in a crown graph is smaller by a factor of 2n than the number of seating arrangements, but larger by a factor of (n − 1)! than the ménage numbers. The sequence of numbers of cycles in these graphs (as before, starting at n = 3) is
- 2, 12, 312, 9600, 416880, 23879520, 1749363840, ... .
A second graph-theoretic description of the problem is also possible. Once the women have been seated, the possible seating arrangements for the remaining men can be described as perfect matchings in a graph formed by removing a single Hamiltonian cycle from a complete bipartite graph; the graph has edges connecting open seats to men, and the removal of the cycle corresponds to forbidding the men to sit in either of the open seats adjacent to their wives. The problem of counting matchings in a bipartite graph, and therefore a fortiori the problem of computing ménage numbers, can be solved using the permanent
Permanent
The permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
s of certain 0-1 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. In the case of the ménage problem, the matrices arising from this view of the problem are circulant matrices
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
.
Knot theory
Tait's motivation for studying the ménage problem came from trying to find a complete listing of mathematical knotKnot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
s with a given number of crossings
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
. In Dowker notation
Dowker notation
thumb|200px|A knot diagram with crossings labelled for a Dowker sequenceIn the mathematical field of knot theory, the Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and...
for knot diagrams, an early form of which was used by Tait, the 2n points where a knot with n knots crosses itself, in consecutive order along the knot, are labeled with the 2n numbers from 1 to 2n. In a reduced diagram, the two labels at a crossing cannot be consecutive, so the set of pairs of labels at each crossing, used in Dowker notation to represent the knot, can be interpreted as a perfect matching in a graph that has a vertex for every number in the range from 1 to 2n and an edge between every pair of numbers that has different parity and are non-consecutive modulo 2n. This graph is formed by removing a Hamiltonian cycle (connecting consecutive numbers) from a complete bipartite graph (connecting all pairs of numbers with different parity), and so it has a number of matchings equal to a ménage number. For alternating knot
Alternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
s, this matching is enough to describe the knot diagram itself; for other knots, an additional positive or negative sign needs to be specified for each crossing pair to determine which of the two strands of the crossing lies above the other strand.
However, the knot listing problem has some additional symmetries not present in the ménage problem: one obtains different Dowker notations for the same knot diagram if one begins the labeling at a different crossing point, and these different notations should all be counted as representing the same diagram. For this reason, two matchings that differ from each other by a cyclic permutation
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
should be treated as equivalent and counted only once. solved this modified enumeration problem, showing that the number of different matchings is
- 1, 2, 5, 20, 87, 616, 4843, 44128, 444621, ... .

