Hot transition
Encyclopedia
In molecular vibration
al spectroscopy, a hot band (or hot transition) is a transition between two states of a single normal mode of vibration, neither of which is the overall ground state
. In infrared
or Raman spectroscopy
, hot bands refer to those transitions for a particular vibrational mode which arise from a state containing thermal population of another vibrational mode. For example, for a molecule with 3 normal mode
s,
, 
and 
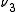, the transition 
← 
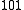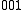, would be a hot band, since the initial state has one quantum of excitation in the 
mode. Hot bands are distinct from combination bands, which involve simultaneous excitation of multiple normal mode
s with a single photon, and overtone
s, which are transitions that involve changing the vibrational quantum number
for a normal mode
by more than 1.
, the normal mode
s of a molecule are not coupled, and all vibrational quantum levels are equally spaced, so hot bands would not be distinguishable from so-called "fundamental" transitions arising from the overall vibrational ground state. However, vibrations of real molecules always have some anharmonicity, which causes coupling between different vibrational modes that in turn shifts the observed frequencies of hot bands in vibrational spectra. Because anharmonicity decreases the spacing between adjacent vibrational levels, hot bands exhibit red shift
s (appear at lower frequencies) than the corresponding fundamental transitions. The magnitude of the observed shift is correlated to the degree of anharmonicity in the corresponding normal mode
s.
Both the lower and upper states involved in the transition are excited states. Therefore, the lower excited state
must be populated for a hot band to be observed. The most common form of excitation is by thermal energy. The population of the lower excited state is then given by the Boltzmann distribution
.
In general the population can be expressed as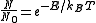
where kB is the Boltzmann constant and E is the energy difference between the two states.
In simplified form this can be expressed as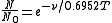
where ν is the wavenumber [cm−1] of the hot band and T is the temperature [K]. Thus, the intensity of a hot band, which is proportional to the population of the lower excited state, increases as the temperature increases.
selection rule
s, but are observed in vibrational spectra of real systems due to anharmonic couplings of normal mode
s. Combination bands typically have weak spectral intensities, but can become quite intense in cases where the anharmonicity of the vibrational potential is large. Broadly speaking, there are two types of combination bands.
← 
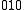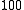, is a difference transition. For difference bands involving transfer of a single quantum of excitation, as in the example, the frequency is approximately equal to the difference between the fundamental frequencies. The difference is not exact because there is anharmonicity in both vibrations. However the term "difference band" also applies to cases where more than one quantum is transferred, such as 
← 
.
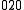Since the initial state of a difference band is always an excited state, difference bands are necessarily "hot bands". Difference bands are seldom observed in conventional vibrational spectra, because they are forbidden transitions according to harmonic selection rules, and because populations of vibrationally excited states tend to be quite low.
← 
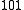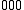and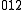 
← 
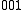, are examples of sum transitions. The frequency of a sum band is slightly less than the sum of the frequencies of the fundamentals, again due to anharmonic shifts in both vibrations.
Sum transitions are harmonic-forbidden, and thus typically have low intensities relative to vibrational fundamentals. Also, sum bands can be, but are not always, hot bands, and thus may also show reduced intensities from thermal population effects, as described above. Sum bands are more commonly observed than difference bands in vibrational spectra
Molecular vibration
A molecular vibration occurs when atoms in a molecule are in periodic motion while the molecule as a whole has constant translational and rotational motion...
al spectroscopy, a hot band (or hot transition) is a transition between two states of a single normal mode of vibration, neither of which is the overall ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
. In infrared
Infrared spectroscopy
Infrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...
or Raman spectroscopy
Raman spectroscopy
Raman spectroscopy is a spectroscopic technique used to study vibrational, rotational, and other low-frequency modes in a system.It relies on inelastic scattering, or Raman scattering, of monochromatic light, usually from a laser in the visible, near infrared, or near ultraviolet range...
, hot bands refer to those transitions for a particular vibrational mode which arise from a state containing thermal population of another vibrational mode. For example, for a molecule with 3 normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
s,
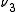, and , the transition 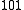← 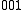, would be a hot band, since the initial state has one quantum of excitation in the mode. Hot bands are distinct from combination bands, which involve simultaneous excitation of multiple normal modeNormal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
s with a single photon, and overtone
Overtone
An overtone is any frequency higher than the fundamental frequency of a sound. The fundamental and the overtones together are called partials. Harmonics are partials whose frequencies are whole number multiples of the fundamental These overlapping terms are variously used when discussing the...
s, which are transitions that involve changing the vibrational quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
for a normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
by more than 1.
Vibrational hot bands
In the harmonic approximationQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
, the normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
s of a molecule are not coupled, and all vibrational quantum levels are equally spaced, so hot bands would not be distinguishable from so-called "fundamental" transitions arising from the overall vibrational ground state. However, vibrations of real molecules always have some anharmonicity, which causes coupling between different vibrational modes that in turn shifts the observed frequencies of hot bands in vibrational spectra. Because anharmonicity decreases the spacing between adjacent vibrational levels, hot bands exhibit red shift
Red shift
-Science:* Redshift, the increase of wavelength of detected electromagnetic radiation with respect to the original wavelength of the emission* Red shift, an informal term for a bathochromic shift...
s (appear at lower frequencies) than the corresponding fundamental transitions. The magnitude of the observed shift is correlated to the degree of anharmonicity in the corresponding normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
s.
Both the lower and upper states involved in the transition are excited states. Therefore, the lower excited state
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
must be populated for a hot band to be observed. The most common form of excitation is by thermal energy. The population of the lower excited state is then given by the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
.
In general the population can be expressed as
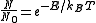
where kB is the Boltzmann constant and E is the energy difference between the two states.
In simplified form this can be expressed as
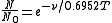
where ν is the wavenumber [cm−1] of the hot band and T is the temperature [K]. Thus, the intensity of a hot band, which is proportional to the population of the lower excited state, increases as the temperature increases.
Combination bands
As mentioned above, combination bands involve changes in vibrational quantum numbers of more than one normal mode. These transitions are forbidden by harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
selection rule
Selection rule
In physics and chemistry a selection rule, or transition rule, formally constrains the possible transitions of a system from one state to another. Selection rules have been derived for electronic, vibrational, and rotational transitions...
s, but are observed in vibrational spectra of real systems due to anharmonic couplings of normal mode
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
s. Combination bands typically have weak spectral intensities, but can become quite intense in cases where the anharmonicity of the vibrational potential is large. Broadly speaking, there are two types of combination bands.
Difference transition
A difference transition, or difference band, occurs between excited states of two different vibrations. Using the 3 mode example from above,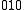 ← 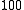, is a difference transition. For difference bands involving transfer of a single quantum of excitation, as in the example, the frequency is approximately equal to the difference between the fundamental frequencies. The difference is not exact because there is anharmonicity in both vibrations. However the term "difference band" also applies to cases where more than one quantum is transferred, such as ← 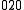.Since the initial state of a difference band is always an excited state, difference bands are necessarily "hot bands". Difference bands are seldom observed in conventional vibrational spectra, because they are forbidden transitions according to harmonic selection rules, and because populations of vibrationally excited states tend to be quite low.
Sum transition
A sum transition (sum band), occurs when two or more fundamental vibrations are excited simultaneously. For instance,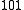 ← 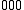and 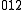← 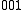, are examples of sum transitions. The frequency of a sum band is slightly less than the sum of the frequencies of the fundamentals, again due to anharmonic shifts in both vibrations.Sum transitions are harmonic-forbidden, and thus typically have low intensities relative to vibrational fundamentals. Also, sum bands can be, but are not always, hot bands, and thus may also show reduced intensities from thermal population effects, as described above. Sum bands are more commonly observed than difference bands in vibrational spectra