
Modes of convergence (annotated index)
Encyclopedia
The purpose of this article is to serve as an annotated
index
of various modes of convergence and their logical relationships. For an expository article, see Modes of convergence
. Simple logical relationships between different modes of convergence are indicated (e.g., if one implies another), formulaically rather than in prose for quick reference, and indepth descriptions and discussions are reserved for their respective articles.
----
Guide to this index. To avoid excessive verbiage, note that each of the following types of objects is a special case of types preceding it: sets, topological spaces, uniform spaces, TAGs
(topological abelian groups), normed spaces
, Euclidean spaces, and the real/complex numbers. Also note that any metric space
is a uniform space. Finally, subheadings will always indicate special cases of their superheadings.
The following is a list of modes of convergence for:
Implications:
- Convergence Cauchy-convergence
Cauchy-convergence
- Cauchy-convergence and convergence of a subsequence together convergence.
convergence.
- U is called "complete" if Cauchy-convergence (for nets) convergence.
convergence.
Note: A sequence exhibiting Cauchy-convergence is called a cauchy sequence to emphasize that it may not be convergent.
Implications:
- Unconditional convergence convergence (by definition).
convergence (by definition).
Implications:
- Absolute-convergence Cauchy-convergence
Cauchy-convergence  absolute-convergence of some grouping1.
absolute-convergence of some grouping1.
- Therefore: N is Banach
(complete) if absolute-convergence convergence.
convergence.
- Absolute-convergence and convergence together unconditional convergence.
unconditional convergence.
- Unconditional convergence absolute-convergence, even if N is Banach.
absolute-convergence, even if N is Banach.
- If N is a Euclidean space, then unconditional convergence absolute-convergence.
absolute-convergence.
1 Note: "grouping" refers to a series obtained by grouping (but not reordering) terms of the original series. A grouping of a series thus corresponds to a subsequence of its partial sums.
Implications are cases of earlier ones, except:
- Uniform convergence both pointwise convergence and uniform Cauchy-convergence.
both pointwise convergence and uniform Cauchy-convergence.
- Uniform Cauchy-convergence and pointwise convergence of a subsequence uniform convergence.
uniform convergence.
Implications:
- "Global" modes of convergence imply the corresponding "local" and "compact" modes of convergence. E.g.:
Uniform convergence both local uniform convergence and compact (uniform) convergence.
both local uniform convergence and compact (uniform) convergence.
- "Local" modes of convergence tend to imply "compact" modes of convergence. E.g.,
Local uniform convergence compact (uniform) convergence.
compact (uniform) convergence.
- If is locally compact, the converses to such tend to hold:
is locally compact, the converses to such tend to hold:
Local uniform convergence compact (uniform) convergence.
compact (uniform) convergence.
Implications:
- Pointwise convergence almost everywhere convergence.
almost everywhere convergence.
- Uniform convergence almost uniform convergence.
almost uniform convergence.
- Almost everywhere convergence convergence in measure. (In a finite measure space)
convergence in measure. (In a finite measure space)
- Almost uniform convergence convergence in measure.
convergence in measure.
- Lp convergence convergence in measure.
convergence in measure.
- Convergence in measure convergence in distribution if μ is a probability measure and the functions are integrable.
convergence in distribution if μ is a probability measure and the functions are integrable.
Implications are all cases of earlier ones.
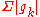 in place of
in place of 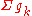 .
.
Implications are cases of earlier ones, except:
- Normal convergence uniform absolute-convergence
uniform absolute-convergence
Implications are all cases of earlier ones.
Implications (mostly cases of earlier ones):
- Uniform absolute-convergence both local uniform absolute-convergence and compact (uniform) absolute-convergence.
both local uniform absolute-convergence and compact (uniform) absolute-convergence.
Normal convergence both local normal convergence and compact normal convergence.
both local normal convergence and compact normal convergence.
- Local normal convergence local uniform absolute-convergence.
local uniform absolute-convergence.
Compact normal convergence compact (uniform) absolute-convergence.
compact (uniform) absolute-convergence.
- Local uniform absolute-convergence compact (uniform) absolute-convergence.
compact (uniform) absolute-convergence.
Local normal convergence compact normal convergence
compact normal convergence
- If X is locally compact:
Local uniform absolute-convergence compact (uniform) absolute-convergence.
compact (uniform) absolute-convergence.
Local normal convergence compact normal convergence
compact normal convergence
Annotation
An annotation is a note that is made while reading any form of text. This may be as simple as underlining or highlighting passages.Annotated bibliographies give descriptions about how each source is useful to an author in constructing a paper or argument...
index
Index (publishing)
An index is a list of words or phrases and associated pointers to where useful material relating to that heading can be found in a document...
of various modes of convergence and their logical relationships. For an expository article, see Modes of convergence
Modes of convergence
In mathematics, there are many senses in which a sequence or a series is said to be convergent. This article describes various modes of convergence in the settings where they are defined...
. Simple logical relationships between different modes of convergence are indicated (e.g., if one implies another), formulaically rather than in prose for quick reference, and indepth descriptions and discussions are reserved for their respective articles.
----
Guide to this index. To avoid excessive verbiage, note that each of the following types of objects is a special case of types preceding it: sets, topological spaces, uniform spaces, TAGs
Topological abelian group
In mathematics, a topological abelian group, or TAG, is a topological group that is also an abelian group.That is, a TAG is both a group and a topological space, the group operations are continuous, and the group's binary operation is commutative....
(topological abelian groups), normed spaces
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, Euclidean spaces, and the real/complex numbers. Also note that any metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is a uniform space. Finally, subheadings will always indicate special cases of their superheadings.
The following is a list of modes of convergence for:
A sequence of elements {an} in a topological space (Y)
- ConvergenceLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
, or "topological convergence" for emphasis (i.e. the existence of a limit).
...in a uniform space (U)
- Cauchy-convergenceCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
Implications:
- Convergence
 Cauchy-convergence
Cauchy-convergence- Cauchy-convergence and convergence of a subsequence together
 convergence.
convergence.- U is called "complete" if Cauchy-convergence (for nets)
 convergence.
convergence.Note: A sequence exhibiting Cauchy-convergence is called a cauchy sequence to emphasize that it may not be convergent.
A series of elements Σbk in a TAG (G)
- ConvergenceLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
(of partial sum sequence) - Cauchy-convergenceCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
(of partial sum sequence) - Unconditional convergence
Implications:
- Unconditional convergence
 convergence (by definition).
convergence (by definition)....in a normed space (N)
- Absolute-convergenceAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
(convergence of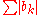 )
)
Implications:
- Absolute-convergence
 Cauchy-convergence
Cauchy-convergence  absolute-convergence of some grouping1.
absolute-convergence of some grouping1.- Therefore: N is Banach
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
(complete) if absolute-convergence
 convergence.
convergence.- Absolute-convergence and convergence together
 unconditional convergence.
unconditional convergence.- Unconditional convergence
 absolute-convergence, even if N is Banach.
absolute-convergence, even if N is Banach.- If N is a Euclidean space, then unconditional convergence
 absolute-convergence.
absolute-convergence.1 Note: "grouping" refers to a series obtained by grouping (but not reordering) terms of the original series. A grouping of a series thus corresponds to a subsequence of its partial sums.
A sequence of functions {fn} from a set (S) to a topological space (Y)
- Pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
...from a set (S) to a uniform space (U)
- Uniform convergence
- Pointwise Cauchy-convergence
- Uniform Cauchy-convergence
Implications are cases of earlier ones, except:
- Uniform convergence
 both pointwise convergence and uniform Cauchy-convergence.
both pointwise convergence and uniform Cauchy-convergence.- Uniform Cauchy-convergence and pointwise convergence of a subsequence
 uniform convergence.
uniform convergence....from a topological space (X) to a uniform space (U)
For many "global" modes of convergence, there are corresponding notions of a) "local" and b) "compact" convergence, which are given by requiring convergence to occur a) on some neighborhood of each point, or b) on all compact subsets of X. Examples:- Local uniform convergence (i.e. uniform convergence on a neighborhood of each point)
- Compact (uniform) convergenceCompact convergenceIn mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
(i.e. uniform convergence on all compact subsets) - further instances of this pattern below.
Implications:
- "Global" modes of convergence imply the corresponding "local" and "compact" modes of convergence. E.g.:
Uniform convergence
 both local uniform convergence and compact (uniform) convergence.
both local uniform convergence and compact (uniform) convergence.- "Local" modes of convergence tend to imply "compact" modes of convergence. E.g.,
Local uniform convergence
 compact (uniform) convergence.
compact (uniform) convergence.- If
 is locally compact, the converses to such tend to hold:
is locally compact, the converses to such tend to hold:Local uniform convergence
 compact (uniform) convergence.
compact (uniform) convergence....from a measure space (S,μ) to the complex numbers (C)
- Almost everywhere convergence
- Almost uniform convergence
- Lp convergence
- Convergence in measureConvergence in measureConvergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
- Convergence in distribution
Implications:
- Pointwise convergence
 almost everywhere convergence.
almost everywhere convergence.- Uniform convergence
 almost uniform convergence.
almost uniform convergence.- Almost everywhere convergence
 convergence in measure. (In a finite measure space)
convergence in measure. (In a finite measure space)- Almost uniform convergence
 convergence in measure.
convergence in measure.- Lp convergence
 convergence in measure.
convergence in measure.- Convergence in measure
 convergence in distribution if μ is a probability measure and the functions are integrable.
convergence in distribution if μ is a probability measure and the functions are integrable.A series of functions Σgk from a set (S) to a TAG (G)
- Pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
(of partial sum sequence) - Uniform convergence (of partial sum sequence)
- Pointwise Cauchy-convergence (of partial sum sequence)
- Uniform Cauchy-convergence (of partial sum sequence)
- Unconditional pointwise convergence
- Unconditional uniform convergence
Implications are all cases of earlier ones.
...from a set (S) to a normed space (N)
Generally, replacing "convergence" by "absolute-convergence" means one is referring to convergence of the series of nonnegative functions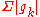 in place of
in place of 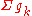 .
.
- Pointwise absolute-convergence (pointwise convergence of
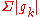 )
) - Uniform absolute-convergenceUniform absolute-convergenceIn mathematics, uniform absolute-convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved when the order of summation is changed.- Motivation :...
(uniform convergence of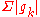 )
) - Normal convergenceNormal convergenceIn mathematics normal convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved when the order of summation is changed.- History :...
http://eom.springer.de/N/n067430.htm (convergence of the series of uniform norms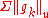 )
)
Implications are cases of earlier ones, except:
- Normal convergence
 uniform absolute-convergence
uniform absolute-convergence...from a topological space (X) to a TAG (G)
- Local uniform convergence (of partial sum sequence)
- Compact (uniform) convergenceCompact convergenceIn mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
(of partial sum sequence)
Implications are all cases of earlier ones.
...from a topological space (X) to a normed space (N)
- Local uniform absolute-convergence
- Compact (uniform) absolute-convergence
- Local normal convergence
- Compact normal convergence
Implications (mostly cases of earlier ones):
- Uniform absolute-convergence
 both local uniform absolute-convergence and compact (uniform) absolute-convergence.
both local uniform absolute-convergence and compact (uniform) absolute-convergence.Normal convergence
 both local normal convergence and compact normal convergence.
both local normal convergence and compact normal convergence.- Local normal convergence
 local uniform absolute-convergence.
local uniform absolute-convergence.Compact normal convergence
 compact (uniform) absolute-convergence.
compact (uniform) absolute-convergence.- Local uniform absolute-convergence
 compact (uniform) absolute-convergence.
compact (uniform) absolute-convergence.Local normal convergence
 compact normal convergence
compact normal convergence- If X is locally compact:
Local uniform absolute-convergence
 compact (uniform) absolute-convergence.
compact (uniform) absolute-convergence.Local normal convergence
 compact normal convergence
compact normal convergence

