Compact convergence
Encyclopedia
In mathematics
compact convergence (or uniform convergence on compact sets) is a type of convergence
which generalizes the idea of uniform convergence. It is associated with the compact-open topology
.
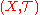be a topological space
and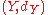
be a metric space
. A sequence of functions
, 
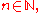
is said to converge compactly as
to some function 
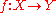if, for every compact set 
,
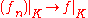
converges uniformly on
as 
. This means that for all compact 
,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
compact convergence (or uniform convergence on compact sets) is a type of convergence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
which generalizes the idea of uniform convergence. It is associated with the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
.
Definition
Let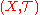 be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and
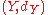be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. A sequence of functions
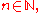
, is said to converge compactly as
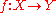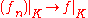
to some function if, for every compact set ,converges uniformly on
as . This means that for all compact ,Examples
- If
and 
with their usual topologies, with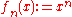 
, then 
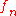converges compactly to the constant function with value 0, but not uniformly.
- If
, 
and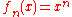 
, then 
converges pointwisePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
to the function that is zero on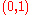
and one at 
, but the sequence does not converge compactly.
- A very powerful tool for showing compact convergence is the Arzelà–Ascoli theorem. There are several versions of this theorem, roughly speaking it states that every sequence of equicontinuous and uniformly bounded maps has a subsequence which converges compactly to some continuous map.
Properties
- If
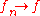uniformly, then 
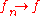compactly. - If
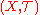is a compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and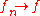
compactly, then 
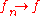uniformly. - If
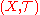is locally compact, then 
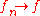compactly if and only if 
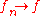locally uniformly. - If
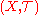is a compactly generated spaceCompactly generated spaceIn topology, a compactly generated space is a topological space whose topology is coherent with the family of all compact subspaces. Specifically, a topological space X is compactly generated if it satisfies the following condition:Equivalently, one can replace closed with open in this definition...
,
compactly, and each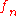 
is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, then
is continuous.