Uniform absolute-convergence
Encyclopedia
In mathematics
, uniform absolute-convergence is a type of convergence for series
of function
s. Like absolute-convergence
, it has the useful property that it is preserved when the order of summation is changed.
precludes this phenomenon. When dealing with uniformly convergent series of functions, the same phenomenon occurs: the series can potentially be reordered into a non-uniformly convergent series, or a series which does not even converge pointwise. This is impossible for series of nonnegative functions, so the notion of uniform absolute-convergence can be used to rule out these possibilities.
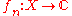(or to any normed vector space
), the series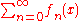
is called uniformly absolutely-convergent if the series of nonnegative functions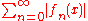
is uniformly convergent.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, uniform absolute-convergence is a type of convergence for series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. Like absolute-convergence
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
, it has the useful property that it is preserved when the order of summation is changed.
Motivation
A convergent series of numbers can often be reordered in such a way that the new series diverges. This is not possible for series of nonnegative numbers, however, so the notion of absolute-convergenceAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
precludes this phenomenon. When dealing with uniformly convergent series of functions, the same phenomenon occurs: the series can potentially be reordered into a non-uniformly convergent series, or a series which does not even converge pointwise. This is impossible for series of nonnegative functions, so the notion of uniform absolute-convergence can be used to rule out these possibilities.
Definition
Given a set S and functions (or to any normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
), the series
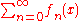
is called uniformly absolutely-convergent if the series of nonnegative functions
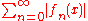
is uniformly convergent.
Distinctions
A series can be uniformly convergent and absolutely convergent without being uniformly absolutely-convergent. For example, if ƒn(x) = xn/n on the open interval (−1,0), then the series Σfn(x) converges uniformly by comparison of the partial sums to those of Σ(−1)n/n, and the series Σ|fn(x)| converges absolutely at each point by the geometric series test, but Σ|fn(x)| does not converge uniformly. Intuitively, this is because the absolute-convergence gets slower and slower as x approaches −1, where convergence holds but absolute convergence fails.Generalizations
If a series of functions is uniformly absolutely-convergent on some neighborhood of each point of a topological space, it is locally uniformly absolutely-convergent. If a series is uniformly absolutely-convergent on all compact subsets of a topological space, it is compactly (uniformly) absolutely-convergent. If the topological space is locally compact, these notions are equivalent.Properties
- If a series of functions into C (or any Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
) is uniformly absolutely-convergent, then it is uniformly convergent. - Uniform absolute-convergence is independent of the ordering of a series. This is because, for a series of nonnegative functions, uniform convergence is equivalent to the property that, for any ε > 0, there are finitely many terms of the series such that excluding these terms results in a series with total sum less than the constant function ε, and this property does not refer to the ordering.