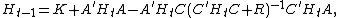Matrix difference equation
Encyclopedia
A matrix difference equation is a difference equation in which the value of a vector (or sometimes, a matrix) of variables at one point in time is related to its own value at one or more previous points in time, using matrices
. Occasionally, the time-varying entity may itself be a matrix instead of a vector. The order of the equation is the maximum time gap between any two indicated values of the variable vector. For example,
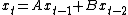
is an example of a second-order matrix difference equation, in which x is an n × 1 vector of variables and A and B are n×n matrices. This equation is homogeneous because there is no vector constant term added to the end of the equation. The same equation might also be written as
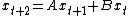
or as
.
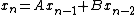The most commonly encountered matrix difference equations are first-order.
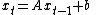
with additive constant vector b. The steady state of this system is a value x* of the vector x which, if reached, would not be deviated from subsequently. x* is found by setting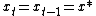
in the difference equation and solving for x* to obtain
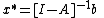
where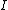
is the n×n identity matrix
, and where it is assumed that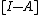
is invertible. Then the non-homogeneous equation can be rewritten in homogeneous form in terms of deviations from the steady state:
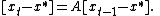
-- that is,
converges asymptotically to the steady state x* -- if and only if all eigenvalues of the transition matrix A (whether real or complex) have an absolute value
which is less than 1.
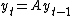. Then we can iterate and substitute repeatedly from the initial condition 
, which is the initial value of the vector y and which must be known in order to find the solution:
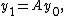
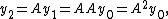
and so forth. By induction
, we obtain the solution in terms of t:
where P is an n × n matrix whose columns are the eigenvectors of A (assuming the eigenvalues are all distinct) and D is an n × n diagonal matrix whose diagonal elements are the eigenvalues of A. This solution motivates the above stability result: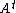
shrinks to the zero matrix over time if and only if the eigenvalues of A are all less than unity in absolute value.
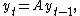we can extract the dynamics of one of the state variables, say 
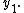The above solution equation for 
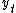shows that the solution for 
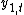is in terms of the n eigenvalues of A. Therefore the equation describing the evolution of 
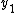by itself must have a solution involving those same eigenvalues. This description intuitively motivates the equation of evolution of 
which is
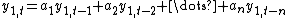
where the parameters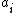
are from the characteristic equation
of the matrix A:
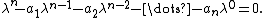
Thus each individual scalar variable of an n-dimensional first-order linear system evolves according to a univariate nth degree difference equation, which has the same stability property (stable or unstable) as does the matrix difference equation.
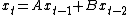
with the variable vector x being n×1 and A and B being n×n. This can be stacked in the form
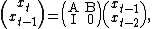
where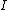
is the n×n identity matrix
and 0 is the n×n zero matrix. Then denoting the 2n×1 stacked vector of current and once-lagged variables as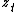
and the 2n×2n block matrix as L, we have as before the solution
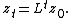
Also as before, this stacked equation and thus the original second-order equation are stable if and only if all eigenvalues of the matrix L are smaller than unity in absolute value.
, there arises a nonlinear matrix equation for the evolution backwards through time of a current-and-future-cost matrix, denoted below as H. This equation is called a discrete dynamic Riccati equation
, and it arises when a variable vector evolving according to a linear matrix difference equation is to be controlled by manipulating an exogenous vector in order to optimize a quadratic
cost function. This Riccati equation assumes the following form or a similar form:
where H, K, and A are n×n, C is n×k, R is k×k, n is the number of elements in the vector to be controlled, and k is the number of elements in the control vector. The parameter matrices A and C are from the linear equation, and the parameter matrices K and R are from the quadratic cost function.
In general this equation cannot be solved analytically for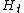
in terms of t ; rather, the sequence of values for 
is found by iterating the Riccati equation. However, it was shown in that this Riccati equation can be solved analytically if R is the zero matrix and n=k+1, by reducing it to a scalar rational difference equation; moreover, for any k and n if the transition matrix A is nonsingular then the Riccati equation can be solved analytically in terms of the eigenvalues of a matrix, although these may need to be found numerically.
In most contexts the evolution of H backwards through time is stable, meaning that H converges to a particular fixed matrix H* which may be irrational even if all the other matrices are rational.
A related Riccati equation is
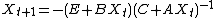
in which the matrices X, A, B, C, and E are all n×n. This equation can be solved explicitly. Suppose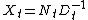
, which certainly holds for t=0 with N0 = X0 and with D0 equal to the identity matrix. Then using this in the difference equation yields
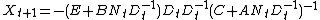
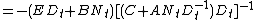
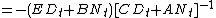
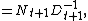
so by induction the form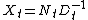
holds for all t. Then the evolution of N and D can be written as
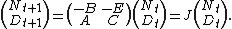
Thus
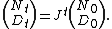
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Occasionally, the time-varying entity may itself be a matrix instead of a vector. The order of the equation is the maximum time gap between any two indicated values of the variable vector. For example,
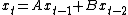
is an example of a second-order matrix difference equation, in which x is an n × 1 vector of variables and A and B are n×n matrices. This equation is homogeneous because there is no vector constant term added to the end of the equation. The same equation might also be written as
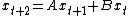
or as
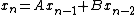.The most commonly encountered matrix difference equations are first-order.
Non-homogeneous first-order matrix difference equations and the steady state
An example of a non-homogeneous first-order matrix difference equation is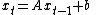with additive constant vector b. The steady state of this system is a value x* of the vector x which, if reached, would not be deviated from subsequently. x* is found by setting
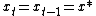in the difference equation and solving for x* to obtain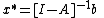where
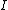is the n×n identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, and where it is assumed that
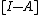is invertible. Then the non-homogeneous equation can be rewritten in homogeneous form in terms of deviations from the steady state: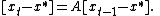Stability of the first-order case
The first-order matrix difference equation [xt - x*] = A[xt-1-x*] is stableStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
-- that is,
converges asymptotically to the steady state x* -- if and only if all eigenvalues of the transition matrix A (whether real or complex) have an absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
which is less than 1.
Solution of the first-order case
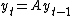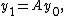
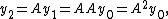
Assume that the equation has been put in the homogeneous form. Then we can iterate and substitute repeatedly from the initial condition , which is the initial value of the vector y and which must be known in order to find the solution:and so forth. By induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, we obtain the solution in terms of t:
where P is an n × n matrix whose columns are the eigenvectors of A (assuming the eigenvalues are all distinct) and D is an n × n diagonal matrix whose diagonal elements are the eigenvalues of A. This solution motivates the above stability result:
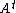shrinks to the zero matrix over time if and only if the eigenvalues of A are all less than unity in absolute value.Extracting the dynamics of a single scalar variable from a first-order matrix system
Starting from the n-dimensional system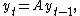 we can extract the dynamics of one of the state variables, say 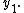The above solution equation for 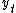shows that the solution for 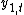is in terms of the n eigenvalues of A. Therefore the equation describing the evolution of 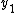by itself must have a solution involving those same eigenvalues. This description intuitively motivates the equation of evolution of which is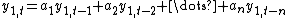where the parameters
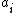are from the characteristic equationCharacteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
of the matrix A:
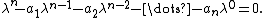
Thus each individual scalar variable of an n-dimensional first-order linear system evolves according to a univariate nth degree difference equation, which has the same stability property (stable or unstable) as does the matrix difference equation.
Solution and stability of higher-order cases
Matrix difference equations of higher order—that is, with a time lag longer than one period—can be solved, and their stability analyzed, by converting them into first-order form using a block matrix. For example, suppose we have the second-order equation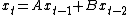with the variable vector x being n×1 and A and B being n×n. This can be stacked in the form
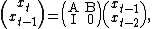
where
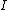is the n×n identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and 0 is the n×n zero matrix. Then denoting the 2n×1 stacked vector of current and once-lagged variables as
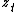and the 2n×2n block matrix as L, we have as before the solution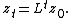Also as before, this stacked equation and thus the original second-order equation are stable if and only if all eigenvalues of the matrix L are smaller than unity in absolute value.
Nonlinear matrix difference equations: Riccati equations
In linear-quadratic-Gaussian controlLinear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
, there arises a nonlinear matrix equation for the evolution backwards through time of a current-and-future-cost matrix, denoted below as H. This equation is called a discrete dynamic Riccati equation
Riccati equation
In mathematics, a Riccati equation is any ordinary differential equation that is quadratic in the unknown function. In other words, it is an equation of the form y' = q_0 + q_1 \, y + q_2 \, y^2...
, and it arises when a variable vector evolving according to a linear matrix difference equation is to be controlled by manipulating an exogenous vector in order to optimize a quadratic
Quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
cost function. This Riccati equation assumes the following form or a similar form:
where H, K, and A are n×n, C is n×k, R is k×k, n is the number of elements in the vector to be controlled, and k is the number of elements in the control vector. The parameter matrices A and C are from the linear equation, and the parameter matrices K and R are from the quadratic cost function.
In general this equation cannot be solved analytically for
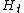in terms of t ; rather, the sequence of values for is found by iterating the Riccati equation. However, it was shown in that this Riccati equation can be solved analytically if R is the zero matrix and n=k+1, by reducing it to a scalar rational difference equation; moreover, for any k and n if the transition matrix A is nonsingular then the Riccati equation can be solved analytically in terms of the eigenvalues of a matrix, although these may need to be found numerically.In most contexts the evolution of H backwards through time is stable, meaning that H converges to a particular fixed matrix H* which may be irrational even if all the other matrices are rational.
A related Riccati equation is
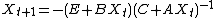
in which the matrices X, A, B, C, and E are all n×n. This equation can be solved explicitly. Suppose
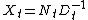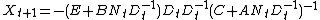
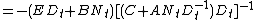
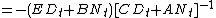
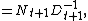
, which certainly holds for t=0 with N0 = X0 and with D0 equal to the identity matrix. Then using this in the difference equation yieldsso by induction the form
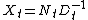holds for all t. Then the evolution of N and D can be written as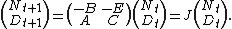Thus
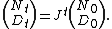
See also
- Matrix differential equationMatrix differential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders...
- Difference equation
- Dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
- Matrix Riccati equation#Mathematical description of the problem and solution