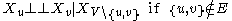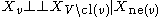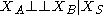Markov network
Encyclopedia
A Markov random field, Markov network or undirected graphical model is a set of variable
s having a Markov property
described by an undirected graph. A Markov random field is similar to a Bayesian network
in its representation of dependencies. It can represent certain dependencies that a Bayesian network cannot (such as cyclic dependencies); on the other hand, it can't represent certain dependencies that a Bayesian network can (such as induced dependencies). The prototypical Markov random field is the Ising model
; indeed, the Markov random field was introduced as the general setting for the Ising model.
A Markov random field is used to model various low- to mid-level tasks in image processing and computer vision. For example, MRFs are used for image restoration
, image completion, segmentation
, texture synthesis
, super-resolution
and stereo matching
.
s X = (Xv)v ∈ V indexed by V form a Markov random field with respect to G if they satisfy the following equivalent Markov properties
:
In other words, a graph G is considered a Markov random field with respect to the joint probability distribution P(X=x) over a set of random variables X if and only if graph separation in G implies conditional independence: If two nodes corresponding to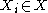
and 
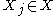are separated in G after removing from G a set of nodes Z, then P(X=x) must assert that 
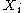and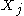 
are conditionally independent given the random variables corresponding to Z. If this condition is satisfied, we say that G is an independency map (or I-Map) of the probability distribution.
Many definitions go even further and require that G be a minimal I-Map, i.e. an I-Map from which none of the edges could be removed without destroying its I-Mapness. (It is reasonable to require this as it leads to the most compact representation, which involves as few dependencies as possible; note that a complete graph is trivially an I-Map.) In the case where G is not only an I-Map (i.e. it represents no independencies that are not indicated by P(X=x)) but also represents no dependencies that are not indicated by P(X=x), G is called a perfect map of P(X=x), as it represents precisely the set of independencies indicated by P(X=x).
Given a set of random variables X = (Xv)v ∈ V for which the joint density
(with respect to a product measure
) can be factorized over the clique
s of G:
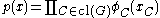
then X forms a Markov random field with respect to G, where cl(G) is the set of cliques of G (the definition is equivalent if only maximal cliques are used). The functions φC are often referred to as factor potentials or clique potentials.
Although some MRFs do not factorize (a simple example can be constructed on a cycle of 4 nodes), in certain cases they can be shown to be equivalent conditions:
When such a factorization does exist, it is possible to construct a factor graph
for the network.
is a Markov random field with feature functions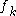
such that the full-joint distribution can be written as
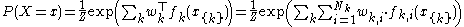
with partition function
.
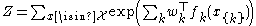where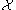
is the set of possible assignments of values to all the network's random variables. Usually, the feature functions 
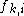are defined such that they are indicators of the clique's configuration, i.e. 
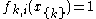if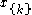 
corresponds to the i-th possible configuration of the k-th clique and 0 otherwise. This model is thus equivalent to the general formulation above if 
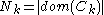and the weight of a feature 
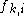corresponds to the logarithm of the corresponding clique potential, i.e. 
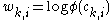, where 
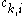is the i-th possible configuration of the k-th clique, i.e. the i-th value in the domain of the clique 
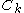. Note that this is only possible if all clique potentials are non-zero, i.e. if none of the elements of 
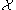are assigned a probability of 0.
Log-linear models are especially convenient for their interpretation. A log-linear model can provide a much more compact representation for many distributions, especially when variables have large domains. They are convenient too because their negative log likelihoods
are convex
. Unfortunately, though the likelihood of a log-linear Markov network is convex, evaluating the likelihood or gradient of the likelihood of a model requires inference in the model, which is in general computationally infeasible.
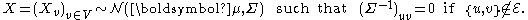
of a set of nodes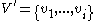
given values to another set of nodes 
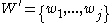in the Markov random field by summing over all possible assignments to 
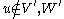; this is called exact inference. However, exact inference is a #P-complete problem, and thus computationally intractable in the general case. Approximation techniques such as Markov chain Monte Carlo
and loopy belief propagation
are often more feasible in practice. Some particular subclasses of MRFs, such as trees see Chow-Liu tree
, have polynomial-time inference algorithms; discovering such subclasses is an active research topic. There are also subclasses of MRFs that permit efficient MAP
, or most likely assignment, inference; examples of these include associative networks.
, in which each random variable may also be conditioned upon a set of global observations
. In this model, each function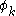 
is a mapping from all assignments to both the clique
k and the observations
to the nonnegative real numbers. This form of the Markov network may be more appropriate for producing discriminative classifiers
, which do not model the distribution over the observations.
Variable
Variable may refer to:* Variable , a logical set of attributes* Variable , a symbol that represents a quantity in an algebraic expression....
s having a Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
described by an undirected graph. A Markov random field is similar to a Bayesian network
Bayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
in its representation of dependencies. It can represent certain dependencies that a Bayesian network cannot (such as cyclic dependencies); on the other hand, it can't represent certain dependencies that a Bayesian network can (such as induced dependencies). The prototypical Markov random field is the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
; indeed, the Markov random field was introduced as the general setting for the Ising model.
A Markov random field is used to model various low- to mid-level tasks in image processing and computer vision. For example, MRFs are used for image restoration
Image restoration
Image restoratio is The operation of taking a corrupted/noisy image and estimating the clean original image. Corruption may come in many forms such as motion blur, noise, and camera misfocus....
, image completion, segmentation
Segmentation
Segmentation may mean:*Market segmentation, in economics and marketingBiology*A process of morphogenesis that divides a metazoan body into a series of semi-repetitive segments*Segmentation , a series of semi-repetitive segments...
, texture synthesis
Texture synthesis
Texture synthesis is the process of algorithmically constructing a large digital image from a small digital sample image by taking advantage of its structural content...
, super-resolution
Super-resolution
Super-resolution are techniques that enhance the resolution of an imaging system. Some SR techniques break the diffraction-limit of systems, while other SR techniques improve over the resolution of digital imaging sensor....
and stereo matching
Computer stereo vision
Computer stereo vision is the extraction of 3D information from digital images, such as obtained by a CCD camera. By comparing information about a scene from two vantage points, 3D information can be extracted by examination of the relative positions of objects in the two panels...
.
Definition
Given an undirected graph G = (V, E), a set of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X = (Xv)v ∈ V indexed by V form a Markov random field with respect to G if they satisfy the following equivalent Markov properties
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
:
- Pairwise Markov property: Any two non-adjacent variables are conditionally independentConditional independenceIn probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
given all other variables:
- Local Markov property: A variable is conditionally independent of all other variables given its neighbours:
-
- where ne(v) is the set of neighbours of v, and cl(v) = {v} ∪ ne(v) is the closed neighbourhood of v.
- Global Markov property: Any two subsets of variables are conditionally independent given a separating subset:
-
- where every path from a node in A to a node in B passes through S.
In other words, a graph G is considered a Markov random field with respect to the joint probability distribution P(X=x) over a set of random variables X if and only if graph separation in G implies conditional independence: If two nodes corresponding to
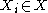and 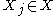are separated in G after removing from G a set of nodes Z, then P(X=x) must assert that 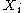and 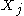are conditionally independent given the random variables corresponding to Z. If this condition is satisfied, we say that G is an independency map (or I-Map) of the probability distribution.Many definitions go even further and require that G be a minimal I-Map, i.e. an I-Map from which none of the edges could be removed without destroying its I-Mapness. (It is reasonable to require this as it leads to the most compact representation, which involves as few dependencies as possible; note that a complete graph is trivially an I-Map.) In the case where G is not only an I-Map (i.e. it represents no independencies that are not indicated by P(X=x)) but also represents no dependencies that are not indicated by P(X=x), G is called a perfect map of P(X=x), as it represents precisely the set of independencies indicated by P(X=x).
Clique factorization
As the Markov properties of an arbitrary probability distribution can be difficult to establish, a commonly used class of Markov random fields are those that can be factorized according to the cliques of the graph.Given a set of random variables X = (Xv)v ∈ V for which the joint density
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(with respect to a product measure
Product measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
) can be factorized over the clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
s of G:
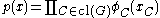
then X forms a Markov random field with respect to G, where cl(G) is the set of cliques of G (the definition is equivalent if only maximal cliques are used). The functions φC are often referred to as factor potentials or clique potentials.
Although some MRFs do not factorize (a simple example can be constructed on a cycle of 4 nodes), in certain cases they can be shown to be equivalent conditions:
- if the density is positive (by the Hammersley–Clifford theoremHammersley–Clifford theoremThe Hammersley–Clifford theorem is a result in probability theory, mathematical statistics and statistical mechanics, that gives necessary and sufficient conditions under which a positive probability distribution can be represented as a Markov network...
), - if the graph is chordalChordal graphIn the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
(by equivalence to a Bayesian networkBayesian networkA Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
).
When such a factorization does exist, it is possible to construct a factor graph
Factor graph
In probability theory and its applications, a factor graph is a particular type of graphical model, with applications in Bayesian inference, that enables efficient computation of marginal distributions through the sum-product algorithm...
for the network.
Log-linear models
A log-linear modelLog-linear model
A log-linear model is a mathematical model that takes the form of a function whose logarithm is a first-degree polynomial function of the parameters of the model, which makes it possible to apply linear regression...
is a Markov random field with feature functions
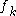such that the full-joint distribution can be written as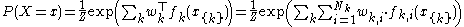with partition function
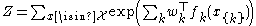.where
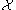is the set of possible assignments of values to all the network's random variables. Usually, the feature functions 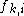are defined such that they are indicators of the clique's configuration, i.e. 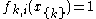if 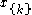corresponds to the i-th possible configuration of the k-th clique and 0 otherwise. This model is thus equivalent to the general formulation above if 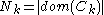and the weight of a feature 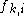corresponds to the logarithm of the corresponding clique potential, i.e. 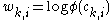, where 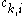is the i-th possible configuration of the k-th clique, i.e. the i-th value in the domain of the clique 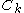. Note that this is only possible if all clique potentials are non-zero, i.e. if none of the elements of 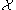are assigned a probability of 0.Log-linear models are especially convenient for their interpretation. A log-linear model can provide a much more compact representation for many distributions, especially when variables have large domains. They are convenient too because their negative log likelihoods
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
are convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
. Unfortunately, though the likelihood of a log-linear Markov network is convex, evaluating the likelihood or gradient of the likelihood of a model requires inference in the model, which is in general computationally infeasible.
Gaussian Markov random field
A multivariate normal distribution forms a Markov random field with respect to a graph G = (V, E) if the missing edges correspond to zeros on the precision matrix (the inverse covariance matrix):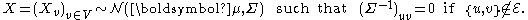Inference
As in a Bayesian network, one may calculate the conditional distributionConditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of a set of nodes
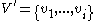given values to another set of nodes 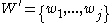in the Markov random field by summing over all possible assignments to 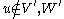; this is called exact inference. However, exact inference is a #P-complete problem, and thus computationally intractable in the general case. Approximation techniques such as Markov chain Monte CarloMarkov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
and loopy belief propagation
Belief propagation
Belief propagation is a message passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node, conditional on any observed nodes...
are often more feasible in practice. Some particular subclasses of MRFs, such as trees see Chow-Liu tree
Chow-Liu tree
A Chow-Liu tree is an efficient method for constructing a second-order product approximation of a joint distribution, first described in a paper by...
, have polynomial-time inference algorithms; discovering such subclasses is an active research topic. There are also subclasses of MRFs that permit efficient MAP
Maximum a posteriori
In Bayesian statistics, a maximum a posteriori probability estimate is a mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data...
, or most likely assignment, inference; examples of these include associative networks.
Conditional random fields
One notable variant of a Markov random field is a conditional random fieldConditional random field
A conditional random field is a statistical modelling method often applied in pattern recognition.More specifically it is a type of discriminative undirected probabilistic graphical model. It is used to encode known relationships between observations and construct consistent interpretations...
, in which each random variable may also be conditioned upon a set of global observations
. In this model, each function 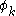is a mapping from all assignments to both the cliqueClique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
k and the observations
to the nonnegative real numbers. This form of the Markov network may be more appropriate for producing discriminative classifiersDiscriminative model
Discriminative models are a class of models used in machine learning for modeling the dependence of an unobserved variable y on an observed variable x...
, which do not model the distribution over the observations.
See also
- Maximum entropy method
- Hopfield network
- Graphical modelGraphical modelA graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
- Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
- Markov logic networkMarkov logic networkA Markov logic network is a probabilistic logic which applies the ideas of a Markov network to first-order logic, enabling uncertain inference...
- Hammersley–Clifford theoremHammersley–Clifford theoremThe Hammersley–Clifford theorem is a result in probability theory, mathematical statistics and statistical mechanics, that gives necessary and sufficient conditions under which a positive probability distribution can be represented as a Markov network...
- Markov-Gibbs properties