
Chow-Liu tree
Encyclopedia
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
, first described in a paper by . The goals of such a decomposition, as with such Bayesian networks in general, may be either data compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
or inference
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
.
The Chow-Liu representation
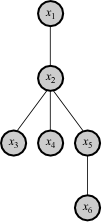
The Chow-Liu method describes a joint probability distribution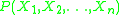 as a product of second-order conditional and marginal distributions. For example, the six-dimensional distribution
as a product of second-order conditional and marginal distributions. For example, the six-dimensional distribution 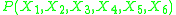 might be approximated as
might be approximated as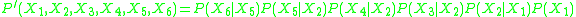
where each new term in the product introduces just one new variable, and the product can be represented as a first-order dependency tree, as shown in the figure. The Chow-Liu algorithm (below) determines which conditional probabilities are to be used in the product approximation. In general, unless there are no third or higher-order interactions, the Chow-Liu approximation is indeed an approximation, and cannot capture the complete structure of the original distribution. provides a modern analysis of the Chow-Liu tree as a Bayesian network
Bayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
.
The Chow-Liu algorithm
Chow and Liu show how to select second-order terms for the product approximation so that among all such second-order approximations (first-order dependency trees), the constructed approximation has the minimum Kullback-Leibler distance to the actual distribution
has the minimum Kullback-Leibler distance to the actual distribution 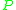 , and is thus the closest approximation in the classical information-theoretic sense. The Kullback-Leibler distance between a second-order product approximation and the actual distribution is shown to be
, and is thus the closest approximation in the classical information-theoretic sense. The Kullback-Leibler distance between a second-order product approximation and the actual distribution is shown to be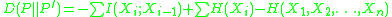
where
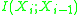 is the mutual information
is the mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between variable
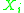 and
and 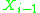 and
and 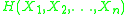 is the joint entropy of variable set
is the joint entropy of variable set  . Since the terms
. Since the terms 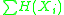 and
and 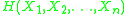 are independent of the dependency ordering in the tree, only the sum of the pairwise mutual information
are independent of the dependency ordering in the tree, only the sum of the pairwise mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
s,
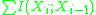 , determines the quality of the approximation. Thus, if every branch (edge) on the tree is given a weight corresponding to the mutual information between the variables at its vertices, then the tree which provides the optimal second-order approximation to the target distribution is just the maximum-weight tree. The equation above also highlights the role of the dependencies in the approximation: When no dependencies exist, and the first term in the equation is absent, we have only an approximation based on first-order marginals, and the distance between the approximation and the true distribution is due to the redundancies that are not accounted for when the variables are treated as independent. As we specify second-order dependencies, we begin to capture some of that structure and reduce the distance between the two distributions.
, determines the quality of the approximation. Thus, if every branch (edge) on the tree is given a weight corresponding to the mutual information between the variables at its vertices, then the tree which provides the optimal second-order approximation to the target distribution is just the maximum-weight tree. The equation above also highlights the role of the dependencies in the approximation: When no dependencies exist, and the first term in the equation is absent, we have only an approximation based on first-order marginals, and the distance between the approximation and the true distribution is due to the redundancies that are not accounted for when the variables are treated as independent. As we specify second-order dependencies, we begin to capture some of that structure and reduce the distance between the two distributions.Chow and Liu provide a simple algorithm for constructing the optimal tree; at each stage of the procedure the algorithm simply adds the maximum mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
pair to the tree. See the original paper, , for full details. A more efficient tree construction algorithm for the common case of sparse data was outlined in .
Chow and Wagner proved in a later paper that the learning of the Chow-Liu tree is consistent given samples (or observations) drawn i.i.d. from a tree-structured distribution. In other words, the probability of learning an incorrect tree decays to zero as the number of samples tends to infinity. The main idea in the proof is the continuity of the mutual information in the pairwise marginal distribution. Recently, the exponential rate of convergence of the error probability was provided.
Variations on Chow-Liu trees
The obvious problem which occurs when the actual distribution is not in fact a second-order dependency tree can still in some cases be addressed by fusing or aggregating together densely connected subsets of variables to obtain a "large-node" Chow-Liu tree , or by extending the idea of greedy maximum branch weight selection to non-tree (multiple parent) structures . (Similar techniques of variable substitution and construction are common in the Bayes network literature, e.g., for dealing with loops. See .)Generalizations of the Chow-Liu tree are the so called t-cherry junction trees. It is proved that the t-cherry junction trees provide a better or at least as good approximation for a discrete multivariate probability distribution as the Chow-Liu tree gives.
For the third order t-cherry junction tree see , for the k-th order t-cherry junction tree see . The second order t-cherry junction tree is in fact the Chow-Liu tree.

