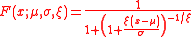Shifted log-logistic distribution
Encyclopedia
The shifted log-logistic distribution is a probability distribution
also known as the generalized log-logistic or the three-parameter log-logistic distribution. It has also been called the generalized logistic distribution, but this conflicts with other uses of the term: see generalized logistic distribution
.
by addition of a shift parameter
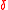 . Thus if
. Thus if  has a log-logistic distribution then
has a log-logistic distribution then  has a shifted log-logistic distribution. So
has a shifted log-logistic distribution. So  has a shifted log-logistic distribution if
has a shifted log-logistic distribution if 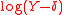 has a logistic distribution. The shift parameter adds a location parameter to the scale and shape parameters of the (unshifted) log-logistic.
has a logistic distribution. The shift parameter adds a location parameter to the scale and shape parameters of the (unshifted) log-logistic.
The properties of this distribution are straightforward to derive from those of the log-logistic distribution. However, an alternative parameterisation, similar to that used for the generalized Pareto distribution and the generalized extreme value distribution, gives more interpretable parameters and also aids their estimation.
In this parameterisation, the cumulative distribution function
of the shifted log-logistic distribution is
for , where
, where 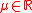 is the location parameter,
is the location parameter,  the scale parameter and
the scale parameter and 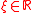 the shape parameter. Note that some references use
the shape parameter. Note that some references use 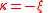 to parameterise the shape.
to parameterise the shape.
The probability density function
is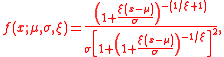
again, for
The shape parameter is often restricted to lie in [-1,1], when the probability density function is bounded. When
is often restricted to lie in [-1,1], when the probability density function is bounded. When  , it has an asymptote
, it has an asymptote
at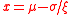 . Reversing the sign of
. Reversing the sign of  reflects the pdf and the cdf about
reflects the pdf and the cdf about  .
.
for modelling flood frequency.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
also known as the generalized log-logistic or the three-parameter log-logistic distribution. It has also been called the generalized logistic distribution, but this conflicts with other uses of the term: see generalized logistic distribution
Generalized logistic distribution
The term generalized logistic distribution is used as the name for several different families of probability distributions. For example, Johnson et al. list four forms, which are listed below. One family described here has also been called the skew-logistic distribution...
.
Definition
The shifted log-logistic distribution can be obtained from the log-logistic distributionLog-logistic distribution
In probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, for example mortality from cancer following...
by addition of a shift parameter
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
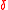 . Thus if
. Thus if  has a log-logistic distribution then
has a log-logistic distribution then  has a shifted log-logistic distribution. So
has a shifted log-logistic distribution. So  has a shifted log-logistic distribution if
has a shifted log-logistic distribution if 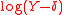 has a logistic distribution. The shift parameter adds a location parameter to the scale and shape parameters of the (unshifted) log-logistic.
has a logistic distribution. The shift parameter adds a location parameter to the scale and shape parameters of the (unshifted) log-logistic.The properties of this distribution are straightforward to derive from those of the log-logistic distribution. However, an alternative parameterisation, similar to that used for the generalized Pareto distribution and the generalized extreme value distribution, gives more interpretable parameters and also aids their estimation.
In this parameterisation, the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the shifted log-logistic distribution is
for
 , where
, where 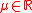 is the location parameter,
is the location parameter,  the scale parameter and
the scale parameter and 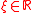 the shape parameter. Note that some references use
the shape parameter. Note that some references use 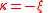 to parameterise the shape.
to parameterise the shape.The probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is
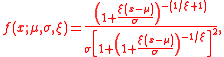
again, for

The shape parameter
 is often restricted to lie in [-1,1], when the probability density function is bounded. When
is often restricted to lie in [-1,1], when the probability density function is bounded. When  , it has an asymptote
, it has an asymptoteAsymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
at
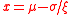 . Reversing the sign of
. Reversing the sign of  reflects the pdf and the cdf about
reflects the pdf and the cdf about  .
.Related distributions
- When
 the shifted log-logistic reduces to the log-logistic distribution.
the shifted log-logistic reduces to the log-logistic distribution. - When
 → 0, the shifted log-logistic reduces to the logistic distribution.
→ 0, the shifted log-logistic reduces to the logistic distribution. - The shifted log-logistic with shape parameter
 is the same as the generalized Pareto distribution with shape parameter
is the same as the generalized Pareto distribution with shape parameter 
Applications
The three-parameter log-logistic distribution is used in hydrologyHydrology
Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
for modelling flood frequency.