
Shanks transformation
Encyclopedia
In numerical analysis
, the Shanks transformation is a non-linear series acceleration
method to increase the rate of convergence
of a sequence
. This method is named after Daniel Shanks
, who rediscovered this sequence transformation in 1955. It was first derived and published by R. Schmidt in 1941.
 the series
the series

is to be determined. First, the partial sum is defined as:
is defined as:
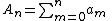
and forms a new sequence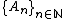 . Provided the series converges,
. Provided the series converges,  will approach in the limit to
will approach in the limit to  as
as 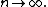
The Shanks transformation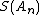 of the sequence
of the sequence 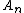 is defined as
is defined as
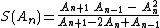
and forms a new sequence. The sequence often converges more rapidly than the sequence
often converges more rapidly than the sequence 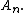
Further speed-up may be obtained by repeated use of the Shanks transformation, by computing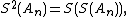
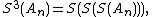 etc.
etc.
Note that the non-linear transformation as used in the Shanks transformation is of similar form as used in Aitken's delta-squared process
. But while Aitken's method operates on the coefficients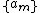 of the original sequence, the Shanks transformation operates on the partial sums
of the original sequence, the Shanks transformation operates on the partial sums 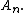
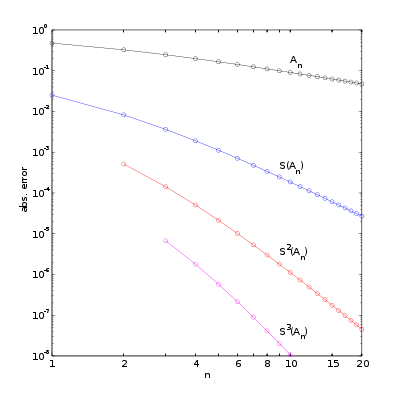 As an example, consider the slowly-convergent series
As an example, consider the slowly-convergent series

which has the exact sum π ≈ 3.14159265. The partial sum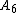 has only one digit accuracy, while six-figure accuracy requires summing about 400,000 terms.
has only one digit accuracy, while six-figure accuracy requires summing about 400,000 terms.
In the table below, the partial sums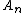 , the Shanks transformation
, the Shanks transformation  on them, as well as the repeated Shanks transformations
on them, as well as the repeated Shanks transformations 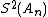 and
and 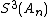 are given for
are given for  up to 12. The figure to the right shows the absolute error for the partial sums and Shanks transformation results, clearly showing the improved accuracy and convergence rate.
up to 12. The figure to the right shows the absolute error for the partial sums and Shanks transformation results, clearly showing the improved accuracy and convergence rate.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Shanks transformation is a non-linear series acceleration
Series acceleration
In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration...
method to increase the rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
. This method is named after Daniel Shanks
Daniel Shanks
Daniel Shanks was an American mathematician who worked primarily in numerical analysis and number theory. He is best known as the first to compute π to 100,000 decimal places, and for his book Solved and Unsolved Problems in Number Theory.-Life and education:Dan Shanks was born on January 17,...
, who rediscovered this sequence transformation in 1955. It was first derived and published by R. Schmidt in 1941.
Formulation
For a sequence the series
the series
is to be determined. First, the partial sum
 is defined as:
is defined as: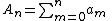
and forms a new sequence
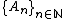 . Provided the series converges,
. Provided the series converges,  will approach in the limit to
will approach in the limit to  as
as 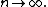
The Shanks transformation
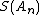 of the sequence
of the sequence 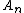 is defined as
is defined as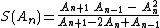
and forms a new sequence. The sequence
 often converges more rapidly than the sequence
often converges more rapidly than the sequence 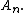
Further speed-up may be obtained by repeated use of the Shanks transformation, by computing
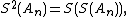
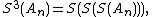 etc.
etc.Note that the non-linear transformation as used in the Shanks transformation is of similar form as used in Aitken's delta-squared process
Aitken's delta-squared process
In numerical analysis, Aitken's delta-squared process is a series acceleration method, used for accelerating the rate of convergence of a sequence. It is named after Alexander Aitken, who introduced this method in 1926. Its early form was known to Seki Kōwa and was found for rectification of the...
. But while Aitken's method operates on the coefficients
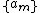 of the original sequence, the Shanks transformation operates on the partial sums
of the original sequence, the Shanks transformation operates on the partial sums 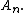
Example


which has the exact sum π ≈ 3.14159265. The partial sum
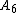 has only one digit accuracy, while six-figure accuracy requires summing about 400,000 terms.
has only one digit accuracy, while six-figure accuracy requires summing about 400,000 terms.In the table below, the partial sums
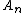 , the Shanks transformation
, the Shanks transformation  on them, as well as the repeated Shanks transformations
on them, as well as the repeated Shanks transformations 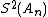 and
and 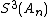 are given for
are given for  up to 12. The figure to the right shows the absolute error for the partial sums and Shanks transformation results, clearly showing the improved accuracy and convergence rate.
up to 12. The figure to the right shows the absolute error for the partial sums and Shanks transformation results, clearly showing the improved accuracy and convergence rate.  |
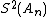 |
transient Transient (oscillation) A transient event is a short-lived burst of energy in a system caused by a sudden change of state.The source of the transient energy may be an internal event or a nearby event... ly to the series result  for for  So for 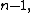  and and 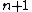 the respective partial sums are: the respective partial sums are: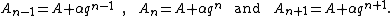 These three equations contain three unknowns: 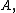  and and 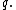 Solving for Solving for 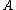 gives gives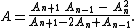 In the (exceptional) case that the denominator is equal to zero: then 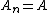 for all for all 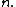 Generalized Shanks transformationThe generalized kth-order Shanks transformation is given as the ratio of the determinantDeterminant In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well... s: 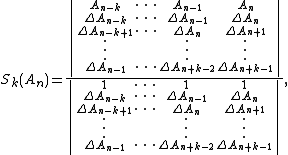 with  It is the solution of a model for the convergence behaviour of the partial sums It is the solution of a model for the convergence behaviour of the partial sums  with with  distinct transients: distinct transients: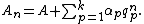 This model for the convergence behaviour contains 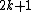 unknowns. By evaluating the above equation at the elements unknowns. By evaluating the above equation at the elements 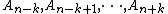 and solving for and solving for  the above expression for the the above expression for the  th-order Shanks transformation is obtained. The first-order generalized Shanks transformation is equal to the ordinary Shanks transformation: th-order Shanks transformation is obtained. The first-order generalized Shanks transformation is equal to the ordinary Shanks transformation:  The generalized Shanks transformation is closely related to Padé approximant Padé approximant Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating.... s and Padé table Padé table In complex analysis, a Padé table is an array, possibly of infinite extent, of the rational Padé approximantsto a given complex formal power series... s. See also
The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

|
|---|
