In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the butterfly lemma or Zassenhaus lemma, named after Hans Julius Zassenhaus

Hans Julius Zassenhaus

Hans Julius Zassenhaus was a German mathematician, known for work in many parts of abstract algebra, and as a pioneer of computer algebra....

, is a technical result on the lattice of subgroups

Lattice of subgroups

In mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial order relation being set inclusion....

 of a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 or the lattice of submodules of a module, or more generally for any modular lattice

Modular lattice

In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨  =  ∧ b,where  ≤  is the partial order, and  ∨  and  ∧  are...

.

Lemma: Suppose 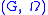is a group with operators

Group with operators

In abstract algebra, a branch of pure mathematics, the algebraic structure group with operators or Ω-group is a group with a set of group endomorphisms.Groups with operators were extensively studied by Emmy Noether and her school in the 1920s...

 and and are subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s. Suppose
and

are stable subgroups. Then,
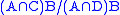is isomorphic

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations.  If there exists an isomorphism between two structures, the two structures are said to be isomorphic.  In a certain sense, isomorphic structures are...

 to

Zassenhaus proved this lemma specifically to give the smoothest proof of the Schreier refinement theorem

Schreier refinement theorem

In mathematics, the Schreier refinement theorem of group theory states that any two normal series of subgroups of a given group have equivalent refinements....

. The 'butterfly' becomes apparent when trying to draw the Hasse diagram

Hasse diagram

In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...

of the various groups involved.

External links

• Zassenhaus Lemma and proof at http://www.artofproblemsolving.com/Wiki/index.php/Zassenhaus%27s_Lemma