Latent Dirichlet allocation
Encyclopedia
In statistics
, latent Dirichlet allocation (LDA) is a generative model
that allows sets of observations to be explained by unobserved
groups that explain why some parts of the data are similar. For example, if observations are words collected into documents, it posits that each document is a mixture of a small number of topics and that each word's creation is attributable to one of the document's topics. LDA is an example of a topic model
and was first presented as a graphical model for topic discovery by David Blei
, Andrew Ng
, and Michael Jordan
in 2002.
of various topics. This is similar to probabilistic latent semantic analysis (pLSA), except that in LDA the topic distribution is assumed to have a Dirichlet prior
. In practice, this results in more reasonable mixtures of topics in a document. It has been noted, however, that the pLSA model is equivalent to the LDA model under a uniform Dirichlet prior distribution.
For example, an LDA model might have topics that can be classified as CAT and DOG. However, the classification is arbitrary because the topic that encompasses these words cannot be named. Furthermore, a topic has probabilities of generating various words, such as milk, meow, and kitten, which can be classified and interpreted by the viewer as "CAT". Naturally, cat itself will have high probability given this topic. The DOG topic likewise has probabilities of generating each word: puppy, bark, and bone might have high probability. Words without special relevance, such as the (see function word
), will have roughly even probability between classes (or can be placed into a separate category).
A document is given the topics. This is a standard bag of words model
assumption, and makes the individual words exchangeable
.
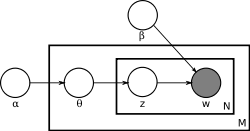With plate notation
, the dependencies among the many variables can be captured concisely. The boxes are “plates” representing replicates. The outer plate represents documents, while the inner plate represents the repeated choice of topics and words within a document. M denotes the number of documents, N the number of words in a document. Thus:
The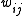
are the only observable variable
s, and the other variables are latent variable
s.
Mostly, the basic LDA model will be extended to a smoothed version to gain better result. The plate notation is shown in the right, where K denotes the number of topics considered in the model and:
The generative process behind is that documents are represented as random mixtures over latent topics, where each topic is characterized by a distribution over words. LDA assumes the following generative process for each document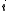
in a corpus D :
1. Choose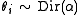
, where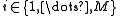 
2. Choose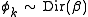
, where 
3. For each of the words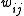
, where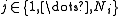 
(Note that the Multinomial distribution here refers to the Multinomial with only one trial. It is formally equivalent to the categorical distribution
.)
The lengths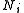
are treated as independent of all the other data generating variables (
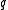and 
). The subscript is often dropped, as in the plate diagrams shown here.
. The original paper used a variational Bayes
approximation of the posterior distribution; alternative inference techniques use Gibbs sampling
and expectation propagation
.
Following is the derivation of the equations for collapsed Gibbs sampling, which means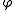
s and
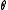s will be integrated out. For simplicity, in this derivation the documents are all assumed to have the same length 
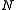. The derivation is equally valid if the document lengths vary.
According to the model, the total probability of the model is:
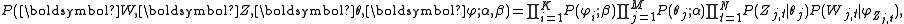
where the bold-font variables denote the vector version of the
variables. First of all,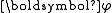
and
need to be integrated out.
Note that all the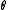
s are independent to each other
and the same to all the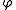
s. So we can treat each
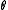and each 
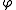separately. We now
focus only on the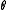
part.
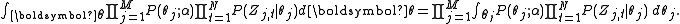
We can further focus on only one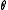
as the
following:
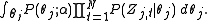
Actually, it is the hidden part of the model for the
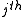document. Now we replace the probabilities in
the above equation by the true distribution expression to write out
the explicit equation.
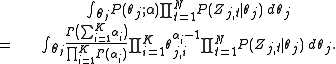
Let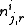
be the number of word tokens in the
document with the same word symbol (the
word in the vocabulary) assigned to the
topic. So,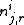 
is three
dimensional. If any of the three dimensions is not limited to a specific value, we use a parenthesized point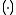
to
denote. For example,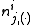
denotes the number
of word tokens in the
document assigned to the
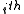topic. Thus, the right most part of the above
equation can be rewritten as:
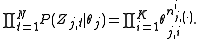
So the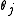
integration formula can be changed to:
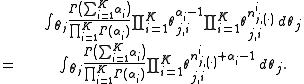
Clearly, the equation inside the integration has the same form as
the Dirichlet distribution. According to the Dirichlet distribution,
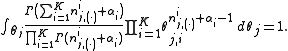
Thus,
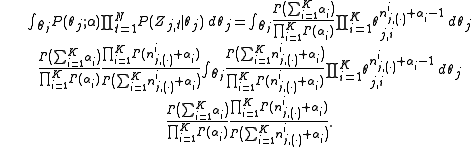
Now we turn our attentions to the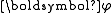
part. Actually, the derivation of the
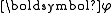part is very similar to the
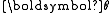part. Here we only list the steps
of the derivation:
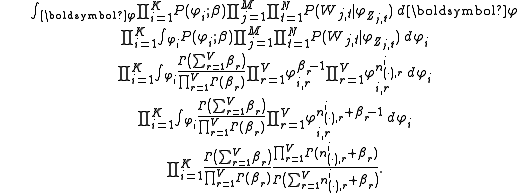
For clarity, here we write down the final equation with both
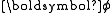and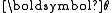 
integrated out:
The goal of Gibbs Sampling here is to approximate the distribution of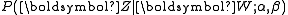
. Since 
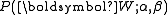is invariable for any of Z, Gibbs Sampling equations can be derived from 
directly. The key point is to derive the following conditional probability:
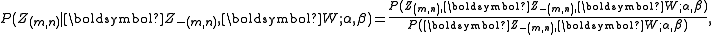
where
denotes the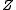 
hidden
variable of the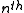
word token in the
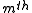document. And further we assume that the word
symbol of it is the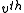
word in the vocabulary.
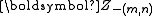denotes all the 
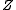s
but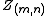
. Note that Gibbs Sampling needs only to
sample a value for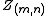
, according to the above
probability, we do not need the exact value of
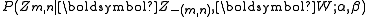but the ratios among the
probabilities that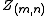
can take value. So, the
above equation can be simplified as:
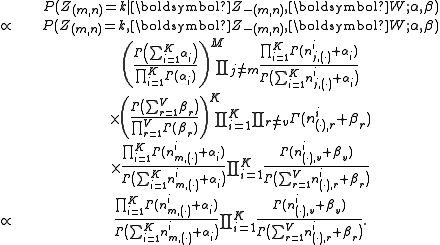
Finally, let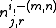
be the same meaning as
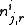but with the 
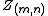excluded.
The above equation can be further simplified by treating terms not
dependent on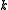
as constants:
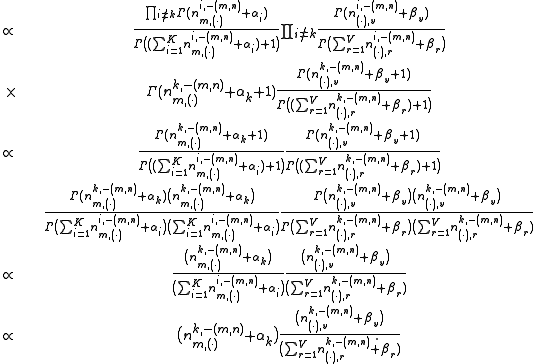
. Related models and techniques are, among others, latent semantic indexing
, independent component analysis
, probabilistic latent semantic indexing, non-negative matrix factorization, Gamma-Poisson.
The LDA model is highly modular and can therefore be easily extended, the main field of interest being the modeling of relations between topics. This is achieved e.g. by using another distribution on the simplex instead of the Dirichlet. The Correlated Topic Model follows this approach, inducing a correlation structure between topics by using the logistic normal distribution instead of the Dirichlet. Another extension is the hierarchical LDA (hLDA), where topics are joined together in a hierarchy by using the nested Chinese restaurant process.
As noted earlier, PLSA is similar to LDA. The LDA model is essentially the Bayesian version of PLSA model. Bayesian formulation tends to perform better on small datasets because Bayesian methods can avoid overfitting the data. In a very large dataset, the results are probably the same. One difference is that PLSA uses a variable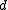
to represent a document in the training set. So in PLSA, when presented with a document the model hasn't seen before, we fix 
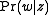--the probability of words under topics—to be that learned from the training set and use the same EM algorithm to infer 
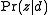--the topic distribution under 
. Blei argues that this step is cheating because you are essentially refitting the model to the new data.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, latent Dirichlet allocation (LDA) is a generative model
Generative model
In probability and statistics, a generative model is a model for randomly generating observable data, typically given some hidden parameters. It specifies a joint probability distribution over observation and label sequences...
that allows sets of observations to be explained by unobserved
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
groups that explain why some parts of the data are similar. For example, if observations are words collected into documents, it posits that each document is a mixture of a small number of topics and that each word's creation is attributable to one of the document's topics. LDA is an example of a topic model
Topic model
In machine learning and natural language processing, a topic model is a type of statistical model for discovering the abstract "topics" that occur in a collection of documents. An early topic model was probabilistic latent semantic indexing , created by Thomas Hofmann in 1999...
and was first presented as a graphical model for topic discovery by David Blei
David Blei
David Blei is an Associate Professor in the Department of Computer Science at Princeton University. His work is primarily in machine learning.His research interests include topic models and he was one of the original developers of latent Dirichlet allocation....
, Andrew Ng
Andrew Ng
Andrew Ng is an Associate Professor in the Department of Computer Science at Stanford University. His work is primarily in machine learning and robotics. He received his PhD from Carnegie Mellon University and finished his postdoctoral research in the University of California, Berkeley, where he...
, and Michael Jordan
Michael I. Jordan
Michael I. Jordan is a leading researcher in machine learning and artificial intelligence. Jordan was a prime mover behind popularising Bayesian networks in the machine learning community and is known for pointing out links between machine learning and statistics...
in 2002.
Topics in LDA
In LDA, each document may be viewed as a mixtureMixture model
In statistics, a mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs...
of various topics. This is similar to probabilistic latent semantic analysis (pLSA), except that in LDA the topic distribution is assumed to have a Dirichlet prior
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
. In practice, this results in more reasonable mixtures of topics in a document. It has been noted, however, that the pLSA model is equivalent to the LDA model under a uniform Dirichlet prior distribution.
For example, an LDA model might have topics that can be classified as CAT and DOG. However, the classification is arbitrary because the topic that encompasses these words cannot be named. Furthermore, a topic has probabilities of generating various words, such as milk, meow, and kitten, which can be classified and interpreted by the viewer as "CAT". Naturally, cat itself will have high probability given this topic. The DOG topic likewise has probabilities of generating each word: puppy, bark, and bone might have high probability. Words without special relevance, such as the (see function word
Function word
Function words are words that have little lexical meaning or have ambiguous meaning, but instead serve to express grammatical relationships with other words within a sentence, or specify the attitude or mood of the speaker...
), will have roughly even probability between classes (or can be placed into a separate category).
A document is given the topics. This is a standard bag of words model
Bag of words model
The bag-of-words model is a simplifying assumption used in natural language processing and information retrieval. In this model, a text is represented as an unordered collection of words, disregarding grammar and even word order.The bag-of-words model is used in some methods of document...
assumption, and makes the individual words exchangeable
De Finetti's theorem
In probability theory, de Finetti's theorem explains why exchangeable observations are conditionally independent given some latent variable to which an epistemic probability distribution would then be assigned...
.
Model
Plate notation
Plate notation is a method of representing variables that repeat in a graphical model. Instead of drawing each repeated variable individually, a plate or rectangle is used to group variables into a subgraph that repeat together, and a number is drawn on the plate to represent the number of...
, the dependencies among the many variables can be captured concisely. The boxes are “plates” representing replicates. The outer plate represents documents, while the inner plate represents the repeated choice of topics and words within a document. M denotes the number of documents, N the number of words in a document. Thus:
- α is the parameter of the Dirichlet prior on the per-document topic distributions.
- β is the parameter of the Dirichlet prior on the per-topic word distribution.
-
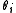is the topic distribution for document i, -
is the word distribution for topic k, -
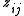is the topic for the jth word in document i, and -
is the specific word.
The
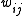are the only observable variableObservable variable
In statistics, observable variables or manifest variables, as opposed to latent variables, are those variables that can be observed and directly measured.- See also :* Observables in physics* Observability in control theory* Latent variable model...
s, and the other variables are latent variable
Latent variable
In statistics, latent variables , are variables that are not directly observed but are rather inferred from other variables that are observed . Mathematical models that aim to explain observed variables in terms of latent variables are called latent variable models...
s.
Mostly, the basic LDA model will be extended to a smoothed version to gain better result. The plate notation is shown in the right, where K denotes the number of topics considered in the model and:
-
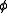is a K*V (V is the dimension of the vocabulary) Markov matrix each row of which denotes the word distribution of a topic.
The generative process behind is that documents are represented as random mixtures over latent topics, where each topic is characterized by a distribution over words. LDA assumes the following generative process for each document
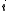in a corpus D :1. Choose
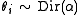, where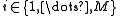 2. Choose
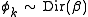, where 3. For each of the words
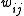, where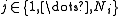 - (a) Choose a topic
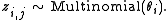
- (b) Choose a word
.
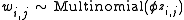(Note that the Multinomial distribution here refers to the Multinomial with only one trial. It is formally equivalent to the categorical distribution
Categorical distribution
In probability theory and statistics, a categorical distribution is a probability distribution that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified...
.)
The lengths
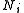are treated as independent of all the other data generating variables ( 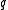and ). The subscript is often dropped, as in the plate diagrams shown here.Inference
Learning the various distributions (the set of topics, their associated word probabilities, the topic of each word, and the particular topic mixture of each document) is a problem of Bayesian inferenceBayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
. The original paper used a variational Bayes
Variational Bayes
Variational Bayesian methods, also called ensemble learning, are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning...
approximation of the posterior distribution; alternative inference techniques use Gibbs sampling
Gibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
and expectation propagation
Expectation propagation
Expectation propagation is a technique in Bayesian machine learning, developed by Thomas Minka.EP finds approximations to a probability distribution. It uses an iterative approach that leverages the factorization structure of the target distribution. It differs from other Bayesian approximation...
.
Following is the derivation of the equations for collapsed Gibbs sampling, which means
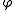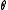s ands will be integrated out. For simplicity, in this derivation the documents are all assumed to have the same length 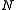. The derivation is equally valid if the document lengths vary.According to the model, the total probability of the model is:
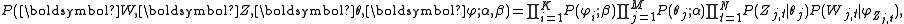
where the bold-font variables denote the vector version of the
variables. First of all,
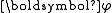and need to be integrated out.Note that all the
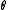s are independent to each otherand the same to all the
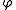s. So we can treat each 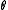and each 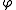separately. We nowfocus only on the
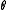part.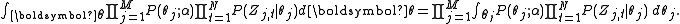We can further focus on only one
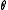as thefollowing:
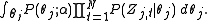
Actually, it is the hidden part of the model for the
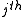document. Now we replace the probabilities inthe above equation by the true distribution expression to write out
the explicit equation.
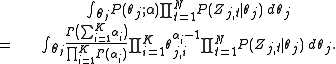
Let
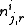be the number of word tokens in the document with the same word symbol (the word in the vocabulary) assigned to the topic. So, 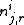is threedimensional. If any of the three dimensions is not limited to a specific value, we use a parenthesized point
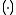todenote. For example,
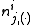denotes the numberof word tokens in the
document assigned to the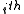 topic. Thus, the right most part of the aboveequation can be rewritten as:
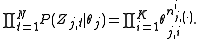
So the
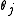integration formula can be changed to: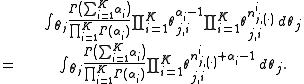Clearly, the equation inside the integration has the same form as
the Dirichlet distribution. According to the Dirichlet distribution,
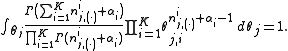
Thus,
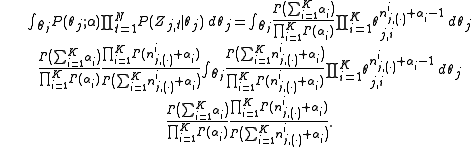
Now we turn our attentions to the
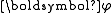
part. Actually, the derivation of the
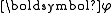part is very similar to the 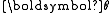part. Here we only list the stepsof the derivation:
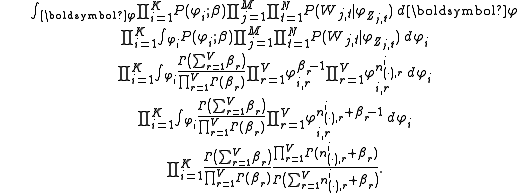
For clarity, here we write down the final equation with both
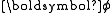and 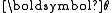integrated out:
The goal of Gibbs Sampling here is to approximate the distribution of
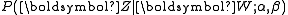. Since 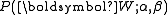is invariable for any of Z, Gibbs Sampling equations can be derived from directly. The key point is to derive the following conditional probability: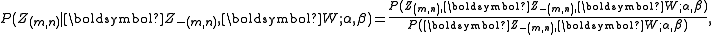where
denotes the 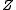hiddenvariable of the
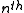word token in the 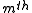document. And further we assume that the wordsymbol of it is the
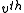word in the vocabulary. 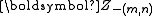denotes all the 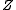sbut
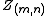. Note that Gibbs Sampling needs only tosample a value for
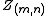, according to the aboveprobability, we do not need the exact value of
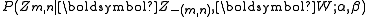but the ratios among theprobabilities that
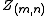can take value. So, theabove equation can be simplified as:
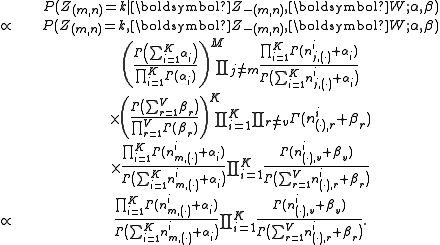
Finally, let
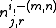be the same meaning as 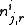but with the 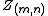excluded.The above equation can be further simplified by treating terms not
dependent on
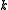as constants: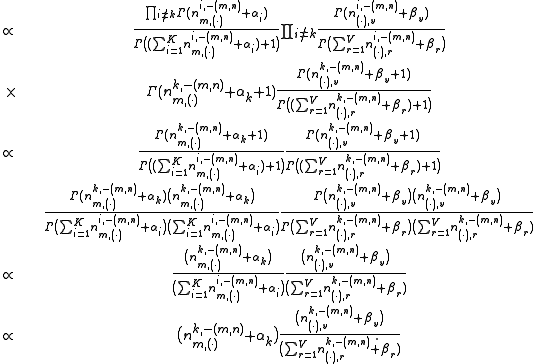Applications, extensions and similar techniques
Topic modeling is a classic problem in information retrievalInformation retrieval
Information retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
. Related models and techniques are, among others, latent semantic indexing
Latent semantic indexing
Latent Semantic Indexing is an indexing and retrieval method that uses a mathematical technique called Singular value decomposition to identify patterns in the relationships between the terms and concepts contained in an unstructured collection of text. LSI is based on the principle that words...
, independent component analysis
Independent component analysis
Independent component analysis is a computational method for separating a multivariate signal into additive subcomponents supposing the mutual statistical independence of the non-Gaussian source signals...
, probabilistic latent semantic indexing, non-negative matrix factorization, Gamma-Poisson.
The LDA model is highly modular and can therefore be easily extended, the main field of interest being the modeling of relations between topics. This is achieved e.g. by using another distribution on the simplex instead of the Dirichlet. The Correlated Topic Model follows this approach, inducing a correlation structure between topics by using the logistic normal distribution instead of the Dirichlet. Another extension is the hierarchical LDA (hLDA), where topics are joined together in a hierarchy by using the nested Chinese restaurant process.
As noted earlier, PLSA is similar to LDA. The LDA model is essentially the Bayesian version of PLSA model. Bayesian formulation tends to perform better on small datasets because Bayesian methods can avoid overfitting the data. In a very large dataset, the results are probably the same. One difference is that PLSA uses a variable
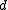to represent a document in the training set. So in PLSA, when presented with a document the model hasn't seen before, we fix 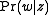--the probability of words under topics—to be that learned from the training set and use the same EM algorithm to infer 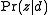--the topic distribution under . Blei argues that this step is cheating because you are essentially refitting the model to the new data.External links
- D. Mimno's LDA Bibliography An exhaustive list of LDA-related resources (incl. papers and some implementations)
- Gensim Python+NumPy implementation of LDA for input larger than the available RAM.
- topicmodels and lda are two RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
packages for LDA analysis. - LDA and Topic Modelling Video Lecture by David Blei
- “Text Mining with R" including LDA methods, video of Rob Zinkov's presentation to the October 2011 meeting of the Los Angeles R users group
- MALLET Open source Java-based package from the University of Massachusetts-Amherst for topic modeling with LDA, also has an independently developed GUI, the Topic Modeling Tool
- LDA in Mahout implementation of LDA using MapReduceMapReduceMapReduce is a software framework introduced by Google in 2004 to support distributed computing on large data sets on clusters of computers. Parts of the framework are patented in some countries....
on the HadoopHadoopApache Hadoop is a software framework that supports data-intensive distributed applications under a free license. It enables applications to work with thousands of nodes and petabytes of data...
platform - The LDA Buffet is Now Open; or, Latent Dirichlet Allocation for English Majors A non-technical introduction to LDA by Matthew Jocker