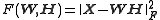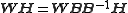Non-negative matrix factorization
Encyclopedia
Non-negative matrix factorization (NMF) is a group of algorithm
s in multivariate analysis
and linear algebra
where a matrix
,
, is factorized into (usually) two matrices, 
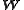and 
: 
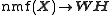
Factorization of matrices is generally non-unique, and a number of different methods of doing so have been developed (e.g. principal component analysis and singular value decomposition
) by incorporating different constraints; non-negative matrix factorization differs from these methods in that it enforces the constraint that the factors W and H must be non-negative, i.e., all elements must be equal to or greater than zero.
non-negative matrix factorization has a long history under the name "self modeling curve resolution".
In this framework the vectors in the right matrix are continuous curves rather than discrete vectors.
Also early work on non-negative matrix factorizations was performed by a Finnish group of researchers in the middle of the 1990s under the name positive matrix factorization.
It became more widely known as non-negative matrix factorization after Lee and Seung investigated
the properties of the algorithm and published some simple and useful
algorithms for two types of factorizations.
When W and H are smaller than X they become easier to store and manipulate.
The different types arise from using different cost functions for measuring the divergence between X and WH and possibly by regularization
of the W and/or H matrices.
Two simple divergence functions studied by Lee and Seung are the squared error (or Frobenius norm) and an extension of the Kullback-Leibler divergence to positive matrices (the original Kullback-Leibler divergence is defined on probability distributions).
Each divergence leads to a different NMF algorithm, usually minimizing the divergence using iterative update rules.
The factorization problem in the squared error version of NMF may be stated as:
Given a matrix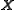
find nonnegative matrices W and H that minimize the function
Another type of NMF for images is based on the total variation norm.
Lee and Seung's updates are usually referred to as the multiplicative update method, while others have suggested gradient descent
algorithms and so-called alternating non-negative least squares and "projected gradient".
The currently available algorithms are sub-optimal as they can only guarantee finding a local minima, rather than a global minimum of the cost function. A provably optimal algorithm is unlikely in the near future as the problem has been shown to generalize the k-means clustering problem which is known to be computationally difficult (NP-complete). However, as in many other data mining applications a local minimum may still prove to be useful.
and principal component analysis, and shows that although the three techniques may be written as factorizations, they implement different constraints and therefore produce different results.
It was later shown that some types of NMF are an instance of a more general probabilistic model called "multinomial PCA".
When NMF is obtained by minimizing the Kullback–Leibler divergence
, it is in fact equivalent to another instance of multinomial PCA, probabilistic latent semantic analysis
,
trained by maximum likelihood
estimation.
That method is commonly used for analyzing and clustering textual data and is also related to the latent class model
.
It has been shown NMF is equivalent to a relaxed form of K-means clustering: matrix factor W contains cluster centroids and H contains cluster
membership indicators, when using the least square as NMF objective. This provides theoretical foundation for using NMF for data clustering.
When using KL divergence as the objective function, it is shown that NMF has a Chi-square interpretation and is equivalent to probabilistic latent semantic analysis
.
NMF extends beyond matrices to tensors of arbitrary order.
This extension may be viewed as a non-negative version of, e.g., the PARAFAC model.
NMF is an instance of the nonnegative quadratic programming
(NQP) as well as many other important problems including the support vector machine
(SVM
). However, SVM
and NMF are related at a more intimate level than that of NQP, which allows direct application of the solution algorithms developed for either of the two methods to problems in both domains.
If the two new matrices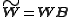
and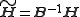 
are non-negative they form another parametrization of the factorization.
The non-negativity of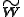
and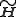 
applies at least if B is a non-negative monomial matrix.
In this simple case it will just correspond to a scaling and a permutation
.
More control over the non-uniqueness of NMF is obtained with sparsity constraints.
applications.
In this process, a document-term matrix
is constructed with the weights of various terms (typically weighted word frequency information) from a set of documents.
This matrix is factored into a term-feature and a feature-document matrix.
The features are derived from the contents of the documents, and the feature-document matrix describes data clusters
of related documents.
One specific application used hierarchical NMF on a small subset of scientific abstracts from PubMed
.
Another research group clustered parts of the Enron
email dataset
with 65,033 messages and 91,133 terms into 50 clusters.
NMF has also been applied to citations data, with one example clustering Wikipedia
articles and scientific journal
s based on the outbound scientific citations in Wikipedia.
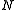hosts, with the help of NMF, the distances of all the 
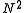end-to-end links can be predicted by conduct only 
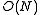measurements. This kind of method was firstly introduced in Internet
Distance Estimation Service (IDES). Afterwards, as a fully decentralized approach, Phoenix network coordinate system
is proposed. It achieves better overall prediction accuracy by introducing the concept of weight.
(1) Algorithmic: searching for global minima of the factors and factor initialization.
(2) Scalability: how to factorize million-by-billion matrices, which are commonplace in Web-scale data mining, e.g., see Distributed Nonnegative Matrix Factorization (DNMF)
(3) Online: how to update the factorization when new data comes in without recomputing from scratch.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s in multivariate analysis
Multivariate analysis
Multivariate analysis is based on the statistical principle of multivariate statistics, which involves observation and analysis of more than one statistical variable at a time...
and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
where a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
,
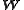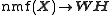
, is factorized into (usually) two matrices, and : Factorization of matrices is generally non-unique, and a number of different methods of doing so have been developed (e.g. principal component analysis and singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
) by incorporating different constraints; non-negative matrix factorization differs from these methods in that it enforces the constraint that the factors W and H must be non-negative, i.e., all elements must be equal to or greater than zero.
History
In chemometricsChemometrics
Chemometrics is the science of extracting information from chemical systems by data-driven means. It is a highly interfacial discipline, using methods frequently employed in core data-analytic disciplines such as multivariate statistics, applied mathematics, and computer science, in order to...
non-negative matrix factorization has a long history under the name "self modeling curve resolution".
In this framework the vectors in the right matrix are continuous curves rather than discrete vectors.
Also early work on non-negative matrix factorizations was performed by a Finnish group of researchers in the middle of the 1990s under the name positive matrix factorization.
It became more widely known as non-negative matrix factorization after Lee and Seung investigated
the properties of the algorithm and published some simple and useful
algorithms for two types of factorizations.
Approximative non-negative matrix factorization
Usually the number of columns of W and the number of rows of H in NMF are selected so the product WH will become an approximation to X (it has been suggested that the NMF model should be called nonnegative matrix approximation instead). The full decomposition of X then amounts to the two non-negative matrices W and H as well as a residual U, such that: X = WH + U. The elements of the residual matrix can either be negative or positive.When W and H are smaller than X they become easier to store and manipulate.
Different cost functions and regularizations
There are different types of non-negative matrix factorizations.The different types arise from using different cost functions for measuring the divergence between X and WH and possibly by regularization
Regularization (mathematics)
In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...
of the W and/or H matrices.
Two simple divergence functions studied by Lee and Seung are the squared error (or Frobenius norm) and an extension of the Kullback-Leibler divergence to positive matrices (the original Kullback-Leibler divergence is defined on probability distributions).
Each divergence leads to a different NMF algorithm, usually minimizing the divergence using iterative update rules.
The factorization problem in the squared error version of NMF may be stated as:
Given a matrix
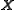find nonnegative matrices W and H that minimize the function
Another type of NMF for images is based on the total variation norm.
Algorithms
There are several ways in which the W and H may be found:Lee and Seung's updates are usually referred to as the multiplicative update method, while others have suggested gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
algorithms and so-called alternating non-negative least squares and "projected gradient".
The currently available algorithms are sub-optimal as they can only guarantee finding a local minima, rather than a global minimum of the cost function. A provably optimal algorithm is unlikely in the near future as the problem has been shown to generalize the k-means clustering problem which is known to be computationally difficult (NP-complete). However, as in many other data mining applications a local minimum may still prove to be useful.
Relation to other techniques
In Learning the parts of objects by non-negative matrix factorization Lee and Seung proposed NMF mainly for parts-based decomposition of images. It compares NMF to vector quantizationVector quantization
Vector quantization is a classical quantization technique from signal processing which allows the modeling of probability density functions by the distribution of prototype vectors. It was originally used for data compression. It works by dividing a large set of points into groups having...
and principal component analysis, and shows that although the three techniques may be written as factorizations, they implement different constraints and therefore produce different results.
It was later shown that some types of NMF are an instance of a more general probabilistic model called "multinomial PCA".
When NMF is obtained by minimizing the Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
, it is in fact equivalent to another instance of multinomial PCA, probabilistic latent semantic analysis
Probabilistic latent semantic analysis
Probabilistic latent semantic analysis , also known as probabilistic latent semantic indexing is a statistical technique for the analysis of two-mode and co-occurrence data. PLSA evolved from latent semantic analysis, adding a sounder probabilistic model...
,
trained by maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimation.
That method is commonly used for analyzing and clustering textual data and is also related to the latent class model
Latent class model
In statistics, a latent class model relates a set of observed discrete multivariate variables to a set of latent variables. It is a type of latent variable model. It is called a latent class model because the latent variable is discrete...
.
It has been shown NMF is equivalent to a relaxed form of K-means clustering: matrix factor W contains cluster centroids and H contains cluster
membership indicators, when using the least square as NMF objective. This provides theoretical foundation for using NMF for data clustering.
When using KL divergence as the objective function, it is shown that NMF has a Chi-square interpretation and is equivalent to probabilistic latent semantic analysis
Probabilistic latent semantic analysis
Probabilistic latent semantic analysis , also known as probabilistic latent semantic indexing is a statistical technique for the analysis of two-mode and co-occurrence data. PLSA evolved from latent semantic analysis, adding a sounder probabilistic model...
.
NMF extends beyond matrices to tensors of arbitrary order.
This extension may be viewed as a non-negative version of, e.g., the PARAFAC model.
NMF is an instance of the nonnegative quadratic programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
(NQP) as well as many other important problems including the support vector machine
Support vector machine
A support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
(SVM
SVM
SVM can refer to:* SVM * Saskatchewan Volunteer Medal* Scanning voltage microscopy* Schuylkill Valley Metro* Secure Virtual Machine, or AMD Virtualization , a virtualization technology by AMD* Solaris Volume Manager...
). However, SVM
SVM
SVM can refer to:* SVM * Saskatchewan Volunteer Medal* Scanning voltage microscopy* Schuylkill Valley Metro* Secure Virtual Machine, or AMD Virtualization , a virtualization technology by AMD* Solaris Volume Manager...
and NMF are related at a more intimate level than that of NQP, which allows direct application of the solution algorithms developed for either of the two methods to problems in both domains.
Uniqueness
The factorization is not unique: A matrix and its inverse can be used to transform the two factorization matrices by, e.g.,
If the two new matrices
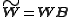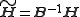and are non-negative they form another parametrization of the factorization.The non-negativity of
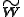and 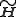applies at least if B is a non-negative monomial matrix.In this simple case it will just correspond to a scaling and a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
.
More control over the non-uniqueness of NMF is obtained with sparsity constraints.
Text mining
NMF can be used for text miningText mining
Text mining, sometimes alternately referred to as text data mining, roughly equivalent to text analytics, refers to the process of deriving high-quality information from text. High-quality information is typically derived through the devising of patterns and trends through means such as...
applications.
In this process, a document-term matrix
Document-term matrix
A document-term matrix or term-document matrix is a mathematical matrix that describes the frequency of terms that occur in a collection of documents. In a document-term matrix, rows correspond to documents in the collection and columns correspond to terms. There are various schemes for determining...
is constructed with the weights of various terms (typically weighted word frequency information) from a set of documents.
This matrix is factored into a term-feature and a feature-document matrix.
The features are derived from the contents of the documents, and the feature-document matrix describes data clusters
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
of related documents.
One specific application used hierarchical NMF on a small subset of scientific abstracts from PubMed
PubMed
PubMed is a free database accessing primarily the MEDLINE database of references and abstracts on life sciences and biomedical topics. The United States National Library of Medicine at the National Institutes of Health maintains the database as part of the Entrez information retrieval system...
.
Another research group clustered parts of the Enron
Enron
Enron Corporation was an American energy, commodities, and services company based in Houston, Texas. Before its bankruptcy on December 2, 2001, Enron employed approximately 22,000 staff and was one of the world's leading electricity, natural gas, communications, and pulp and paper companies, with...
email dataset
with 65,033 messages and 91,133 terms into 50 clusters.
NMF has also been applied to citations data, with one example clustering Wikipedia
Wikipedia
Wikipedia is a free, web-based, collaborative, multilingual encyclopedia project supported by the non-profit Wikimedia Foundation. Its 20 million articles have been written collaboratively by volunteers around the world. Almost all of its articles can be edited by anyone with access to the site,...
articles and scientific journal
Scientific journal
In academic publishing, a scientific journal is a periodical publication intended to further the progress of science, usually by reporting new research. There are thousands of scientific journals in publication, and many more have been published at various points in the past...
s based on the outbound scientific citations in Wikipedia.
Spectral data analysis
NMF is also used to analyze spectral data; one such use is in the classification of space objects and debris.Scalable Internet distance prediction
NMF is applied in scalable Internet distance (round-trip time) prediction. For a network with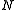 hosts, with the help of NMF, the distances of all the 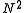end-to-end links can be predicted by conduct only 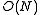measurements. This kind of method was firstly introduced in InternetDistance Estimation Service (IDES). Afterwards, as a fully decentralized approach, Phoenix network coordinate system
is proposed. It achieves better overall prediction accuracy by introducing the concept of weight.
Current research
Current research in nonnegative matrix factorization includes, but not limited to,(1) Algorithmic: searching for global minima of the factors and factor initialization.
(2) Scalability: how to factorize million-by-billion matrices, which are commonplace in Web-scale data mining, e.g., see Distributed Nonnegative Matrix Factorization (DNMF)
(3) Online: how to update the factorization when new data comes in without recomputing from scratch.
Software
- Routines for performing Weighted Non-Negative Matrix Factorzation
- Non-negative Matrix Factorization R (programming language)R (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
implementation by Suhai (Timothy) Liu. - Non-negative Matrix Factorization: algorithms and development framework R (programming language)R (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
: R-package published on CRANCranCran may refer to:*CRAN , the Comprehensive R Archive Network for the R programming language*Cran , a measurement of uncleaned herring*Cranberry, a fruit...
that implements a number of NMF algorithms and provides a framework to test, develop and benchmark new/custom algorithms. [by Renaud Gaujoux]. - Fast Non-Negative Matrix Factorization Software An efficient and feature rich C++ implementation of NMF using alternating non-negative least squares (ANLS) framework and block coordinate descent approach.
- NMF toolbox implemented in Matlab. Developed at IMM DTU.
- Text to Matrix Generator (TMG) MATLAB toolbox that can be used for various tasks in text mining (TM) specifically i) indexing, ii) retrieval, iii) dimensionality reduction, iv) clustering, v) classification. Most of TMG is written in MATLAB and parts in Perl. It contains implementations of LSI, clustered LSI, NMF and other methods.
- GraphLab Efficient non-negative matrix factorization on multicore.