Zwanzig projection operator
Encyclopedia
The Zwanzig projection operator is a mathematical device used in statistical mechanics
.
It operates in the linear space of phase space
functions and projects onto the linear subspace of "slow"
phase space functions. It was introduced by R. Zwanzig to derive a generic master equation
. It is
mostly used in this or similar context in a formal way to derive equations of motion for some "slow"
collective variables.
A special subset of these functions is an enumerable set of "slow variables" A(q)={(An(q)}. Candidates for some of these variables might be the long-wavelength Fourier components ρk(q) of the mass density and the long-wavelength Fourier components πk(q) of the momentum density with the wave vector k identified with n. The Zwanzig projection operator relies on these functions but doesn't tell how to find the slow variables of a given Hamiltonian
H(q).
A projection operator requires a scalar product. A scalar product between two arbitrary phase space functions f1(q) and f2(q) is defined by the equilibrium correlation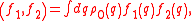
where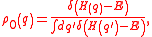
denotes the microcanonical
equilibrium distribution. "Fast" variables, by definition, are orthogonal to all functions G(A(q)) of A(q) under this scalar product. This definition states that fluctuations of fast and slow variables are uncorrelated. If a generic function f(q) is correlated with some slow variables, then one may subtract functions of slow variables until there remains the uncorrelated fast part of f(q). The product of a slow and a fast variable is a fast variable.
A generic phase space function f(q) decomposes according to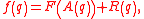
where R(q) is the fast part of f(q). To get an expression for the slow part F(A(q)) of f take the scalar product with the slow function δ(A(q) - a),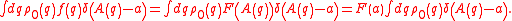
This gives an expression for F(a), and thus for the operator P projecting an arbitrary function f(q) to its "slow" part depending on q only through A(q),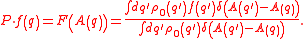
This expression agrees with the expression given by Zwanzig, except that Zwanzig subsumes H(q) in the slow variables. The Zwanzig projection operator fulfills PG(A(q)) = G(A(q) and P2 = P. The fast part of f(q) is (1-P)f(q).
it allows to derive a master equation for the time dependent probability
distribution p(a,t) of the slow variables (or Langevin equations for the slow variables themselves).
To sketch the typical steps, let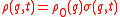
denote the time-dependent probability distribution in phase space.
The phase space density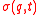
(as well as 
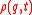) is a
solution of the Liouville equation
The crucial step then is to write
, 
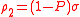
and to project the Liouville equation onto the slow and
the fast subspace,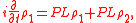
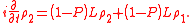
Solving the second equation for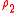
and inserting 
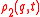into the first
equation gives a closed equation for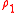
.
The latter equation finally gives an equation for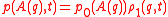
,
where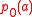
denotes the equilibrium distribution of the slow variables.
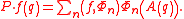
A special choice for Φn(A(q)) are orthonormalized linear combinations of the slow variables A(q). This leads to the Mori projection operator. However, the set of linear functions isn't complete, and the orthogonal variables aren't fast or random if nonlinearity in A comes into play.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
It operates in the linear space of phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
functions and projects onto the linear subspace of "slow"
phase space functions. It was introduced by R. Zwanzig to derive a generic master equation
Master equation
In physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
. It is
mostly used in this or similar context in a formal way to derive equations of motion for some "slow"
collective variables.
Slow variables and scalar product
The Zwanzig projection operator operates on functions in the 6-N-dimensional phase space q={xi, pi} of N point partices with coordinates xi and momenta pi.A special subset of these functions is an enumerable set of "slow variables" A(q)={(An(q)}. Candidates for some of these variables might be the long-wavelength Fourier components ρk(q) of the mass density and the long-wavelength Fourier components πk(q) of the momentum density with the wave vector k identified with n. The Zwanzig projection operator relies on these functions but doesn't tell how to find the slow variables of a given Hamiltonian
Hamiltonian
Hamiltonian may refer toIn mathematics :* Hamiltonian system* Hamiltonian path, in graph theory** Hamiltonian cycle, a special case of a Hamiltonian path* Hamiltonian group, in group theory* Hamiltonian...
H(q).
A projection operator requires a scalar product. A scalar product between two arbitrary phase space functions f1(q) and f2(q) is defined by the equilibrium correlation
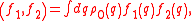
where
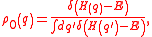
denotes the microcanonical
Microcanonical ensemble
In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...
equilibrium distribution. "Fast" variables, by definition, are orthogonal to all functions G(A(q)) of A(q) under this scalar product. This definition states that fluctuations of fast and slow variables are uncorrelated. If a generic function f(q) is correlated with some slow variables, then one may subtract functions of slow variables until there remains the uncorrelated fast part of f(q). The product of a slow and a fast variable is a fast variable.
The projection operator
Consider the continuous set of functions Φa(q) = δ(A(q) - a) = Πnδ(An(q)-an) with a = {an} constant. Any phase space function G(A(q)) depending on q only through A(q) is a function of the Φa, namelyA generic phase space function f(q) decomposes according to
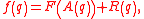
where R(q) is the fast part of f(q). To get an expression for the slow part F(A(q)) of f take the scalar product with the slow function δ(A(q) - a),
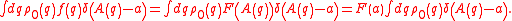
This gives an expression for F(a), and thus for the operator P projecting an arbitrary function f(q) to its "slow" part depending on q only through A(q),
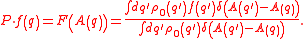
This expression agrees with the expression given by Zwanzig, except that Zwanzig subsumes H(q) in the slow variables. The Zwanzig projection operator fulfills PG(A(q)) = G(A(q) and P2 = P. The fast part of f(q) is (1-P)f(q).
Connection with Liouville and Master equation
The ultimate justification for the definition of P as given above is thatit allows to derive a master equation for the time dependent probability
distribution p(a,t) of the slow variables (or Langevin equations for the slow variables themselves).
To sketch the typical steps, let
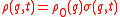
denote the time-dependent probability distribution in phase space.
The phase space density
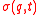(as well as 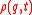) is asolution of the Liouville equation
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
The crucial step then is to write
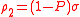
, and to project the Liouville equation onto the slow and
the fast subspace,
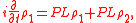
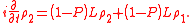
Solving the second equation for
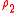and inserting 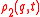into the firstequation gives a closed equation for
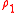.The latter equation finally gives an equation for
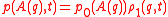,where
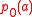denotes the equilibrium distribution of the slow variables.Discrete set of functions, relation to the Mori projection operator
Instead of expanding the slow part of f(q) in the continuous set Φa(q) = δ(A(q) - a) of functions one also might use some enumerable set of functions Φn(A(q)). If these functions constitute a complete orthonormal function set then the projection operator simply reads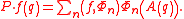A special choice for Φn(A(q)) are orthonormalized linear combinations of the slow variables A(q). This leads to the Mori projection operator. However, the set of linear functions isn't complete, and the orthogonal variables aren't fast or random if nonlinearity in A comes into play.