Langevin dynamics
Encyclopedia
In physics
, Langevin dynamics is an approach to the mathematical modeling of the dynamics of molecular systems, originally developed by the French physicist Paul Langevin
. The approach is characterized by the use of simplified models while accounting for omitted degrees of freedom
by the use of stochastic differential equation
s.
A molecular system in the real world is unlikely to be present in vacuum. Jostling of solvent or air molecules causes friction, and the occasional high velocity collision will perturb the system. Langevin dynamics attempts to extend molecular dynamics
to allow for these effects. Also, Langevin dynamics allows controlling the temperature like a thermostat, thus approximating the canonical ensemble
.
Langevin dynamics mimics the viscous aspect of a solvent. It does not fully model an implicit solvent; specifically, the model does not account for the electrostatic screening
and also not for the hydrophobic effect
.
For a system of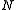
particles with masses 
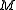, with coordinates 
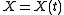that constitute a time-dependent random variable
, the resulting Langevin equation
is
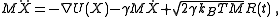
where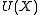
is the particle interaction potential; 
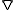is the gradient operator such that 
is the force calculated from the particle interaction potentials; the dot is a time derivative such that 
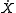is the velocity and 
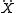is the acceleration; T is the temperature, kB is Boltzmann's constant; and 
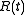is a delta-correlated stationary
Gaussian process
with zero-mean, satisfying
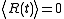
Here,
is the Dirac delta.
If the main objective is to control temperature, care should be exercised to use a small damping constant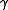
. As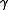 
grows, it spans the inertial all the way to the diffusive (Brownian
) regime. The Langevin dynamics limit of non-inertia is commonly described as Brownian dynamics.
The Langevin equation can be
reformulated as a Fokker–Planck equation that governs the probability distribution
of the random variable X.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Langevin dynamics is an approach to the mathematical modeling of the dynamics of molecular systems, originally developed by the French physicist Paul Langevin
Paul Langevin
Paul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
. The approach is characterized by the use of simplified models while accounting for omitted degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
by the use of stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
s.
A molecular system in the real world is unlikely to be present in vacuum. Jostling of solvent or air molecules causes friction, and the occasional high velocity collision will perturb the system. Langevin dynamics attempts to extend molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
to allow for these effects. Also, Langevin dynamics allows controlling the temperature like a thermostat, thus approximating the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
.
Langevin dynamics mimics the viscous aspect of a solvent. It does not fully model an implicit solvent; specifically, the model does not account for the electrostatic screening
Poisson-Boltzmann equation
The Poisson–Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy–Chapman double layer theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913...
and also not for the hydrophobic effect
Hydrophobic effect
The hydrophobic effect is the observed tendency of nonpolar substances to aggregate in aqueous solution and exclude water molecules. The name, literally meaning "water-fearing," describes the segregation and apparent repulsion between water and nonpolar substances...
.
For a system of
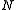particles with masses 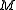, with coordinates 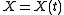that constitute a time-dependent random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, the resulting Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
is
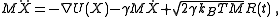
where
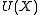is the particle interaction potential; 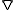is the gradient operator such that is the force calculated from the particle interaction potentials; the dot is a time derivative such that 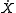is the velocity and 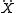is the acceleration; T is the temperature, kB is Boltzmann's constant; and 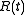is a delta-correlated stationaryStationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
with zero-mean, satisfying
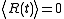
Here,
is the Dirac delta.If the main objective is to control temperature, care should be exercised to use a small damping constant
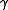. As 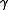grows, it spans the inertial all the way to the diffusive (BrownianBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) regime. The Langevin dynamics limit of non-inertia is commonly described as Brownian dynamics.
The Langevin equation can be
reformulated as a Fokker–Planck equation that governs the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the random variable X.
See also
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Molecular dynamicsMolecular dynamicsMolecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
- Brownian dynamics
- Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
- Implicit solvationImplicit solvationImplicit solvation is a method of representing solvent as a continuous medium instead of individual “explicit” solvent molecules most often used in molecular dynamics simulations and in other applications of molecular mechanics...
- Stochastic differential equations
- Langevin equationLangevin equationIn statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...