
Kosmann lift
Encyclopedia
In differential geometry, the Kosmann lift, named after Yvette Kosmann-Schwarzbach, of a vector field 
on a Riemannian manifold
 is the canonical projection
is the canonical projection  on the orthonormal frame bundle of its natural lift
on the orthonormal frame bundle of its natural lift  defined on the bundle of linear frames.
defined on the bundle of linear frames.
Generalisations exist for any given reductive G-structure
.
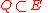 of a fiber bundle
of a fiber bundle
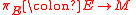 over
over 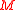 and a vector field
and a vector field  on
on  , its restriction
, its restriction  to
to  is a vector field "along"
is a vector field "along"  not on (i.e., tangent to)
not on (i.e., tangent to)  . If one denotes by
. If one denotes by  the canonical embedding
the canonical embedding
, then is a section
is a section
of the pullback bundle
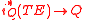 , where
, where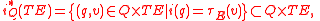
and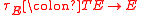 is the tangent bundle
is the tangent bundle
of the fiber bundle .
.
Let us assume that we are given a Kosmann decomposition of the pullback bundle , such that
, such that
i.e., at each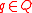 one has
one has 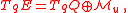 where
where 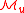 is a vector subspace of
is a vector subspace of 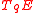 and we assume
and we assume 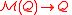 to be a vector bundle
to be a vector bundle
over , called the transversal bundle of the Kosmann decomposition. It follows that the restriction
, called the transversal bundle of the Kosmann decomposition. It follows that the restriction  to
to  splits into a tangent vector field
splits into a tangent vector field 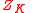 on
on  and a transverse vector field
and a transverse vector field  being a section of the vector bundle
being a section of the vector bundle 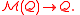
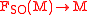 be the oriented orthonormal frame bundle of an oriented
be the oriented orthonormal frame bundle of an oriented  -dimensional
-dimensional
Riemannian manifold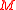 with given metric
with given metric 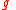 . This is a principal
. This is a principal  -subbundle of
-subbundle of 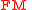 , the tangent frame bundle of linear frames over
, the tangent frame bundle of linear frames over 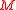 with structure group
with structure group 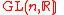 .
.
By definition, one may say that we are given with a classical reductive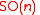 -structure. The special orthogonal group
-structure. The special orthogonal group 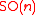 is a reductive Lie subgroup of
is a reductive Lie subgroup of 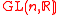 . In fact, there exists a direct sum
. In fact, there exists a direct sum
decomposition , where
, where 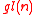 is the Lie algebra of
is the Lie algebra of 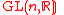 ,
, 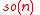 is the Lie algebra of
is the Lie algebra of 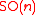 , and
, and  is the
is the 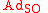 -invariant vector subspace of symmetric matrices, i.e.
-invariant vector subspace of symmetric matrices, i.e.  for all
for all 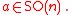
Let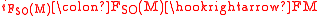 be the canonical embedding
be the canonical embedding
.
One then can prove that there exists a canonical Kosmann decomposition of the pullback bundle
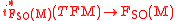 such that
such that

i.e., at each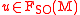 one has
one has 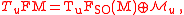
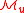 being the fiber over
being the fiber over  of the subbundle
of the subbundle
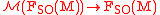 of
of 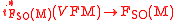 . Here,
. Here,  is the vertical subbundle of
is the vertical subbundle of  and at each
and at each 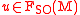 the fiber
the fiber 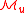 is isomorphic to the vector space
is isomorphic to the vector space
of symmetric matrices .
.
From the above canonical and equivariant
decomposition, it follows that the restriction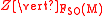 of an
of an 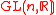 -invariant vector field
-invariant vector field  on
on 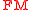 to
to 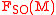 splits into a
splits into a  -invariant vector field
-invariant vector field 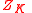 on
on  , called the Kosmann vector field associated with
, called the Kosmann vector field associated with  , and a transverse vector field
, and a transverse vector field  .
.
In particular, for a generic vector field
 on the base manifold
on the base manifold  , it follows that the restriction
, it follows that the restriction 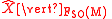 to
to 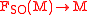 of its natural lift
of its natural lift  onto
onto  splits into a
splits into a  -invariant vector field
-invariant vector field 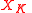 on
on 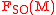 , called the Kosmann lift of
, called the Kosmann lift of  , and a transverse vector field
, and a transverse vector field 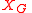 called the von Göden lift of
called the von Göden lift of 

on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
 is the canonical projection
is the canonical projection  on the orthonormal frame bundle of its natural lift
on the orthonormal frame bundle of its natural lift  defined on the bundle of linear frames.
defined on the bundle of linear frames.Generalisations exist for any given reductive G-structure
G-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
.
Introduction
In general, given a subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
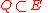 of a fiber bundle
of a fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
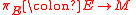 over
over 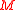 and a vector field
and a vector field  on
on  , its restriction
, its restriction  to
to  is a vector field "along"
is a vector field "along"  not on (i.e., tangent to)
not on (i.e., tangent to)  . If one denotes by
. If one denotes by  the canonical embedding
the canonical embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
, then
 is a section
is a sectionSection
Section may refer to:* Section * Section * Archaeological section* Histological section, a thin slice of tissue used for microscopic examination* Section, an instrumental group within an orchestra...
of the pullback bundle
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
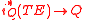 , where
, where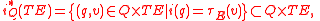
and
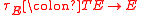 is the tangent bundle
is the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of the fiber bundle
 .
.Let us assume that we are given a Kosmann decomposition of the pullback bundle
 , such that
, such that
i.e., at each
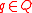 one has
one has 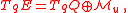 where
where 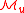 is a vector subspace of
is a vector subspace of 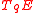 and we assume
and we assume 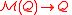 to be a vector bundle
to be a vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over
 , called the transversal bundle of the Kosmann decomposition. It follows that the restriction
, called the transversal bundle of the Kosmann decomposition. It follows that the restriction  to
to  splits into a tangent vector field
splits into a tangent vector field 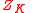 on
on  and a transverse vector field
and a transverse vector field  being a section of the vector bundle
being a section of the vector bundle 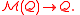
Definition
Let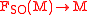 be the oriented orthonormal frame bundle of an oriented
be the oriented orthonormal frame bundle of an oriented  -dimensional
-dimensionalRiemannian manifold
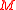 with given metric
with given metric 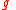 . This is a principal
. This is a principal  -subbundle of
-subbundle of 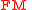 , the tangent frame bundle of linear frames over
, the tangent frame bundle of linear frames over 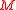 with structure group
with structure group 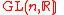 .
.By definition, one may say that we are given with a classical reductive
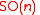 -structure. The special orthogonal group
-structure. The special orthogonal group 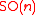 is a reductive Lie subgroup of
is a reductive Lie subgroup of 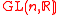 . In fact, there exists a direct sum
. In fact, there exists a direct sumDirect sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
decomposition
 , where
, where 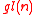 is the Lie algebra of
is the Lie algebra of 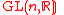 ,
, 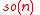 is the Lie algebra of
is the Lie algebra of 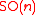 , and
, and  is the
is the 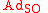 -invariant vector subspace of symmetric matrices, i.e.
-invariant vector subspace of symmetric matrices, i.e.  for all
for all 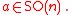
Let
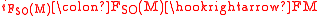 be the canonical embedding
be the canonical embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
.
One then can prove that there exists a canonical Kosmann decomposition of the pullback bundle
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
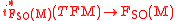 such that
such that
i.e., at each
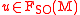 one has
one has 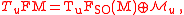
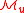 being the fiber over
being the fiber over  of the subbundle
of the subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
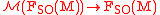 of
of 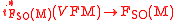 . Here,
. Here,  is the vertical subbundle of
is the vertical subbundle of  and at each
and at each 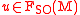 the fiber
the fiber 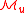 is isomorphic to the vector space
is isomorphic to the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of symmetric matrices
 .
.From the above canonical and equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
decomposition, it follows that the restriction
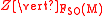 of an
of an 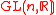 -invariant vector field
-invariant vector field  on
on  to
to 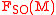 splits into a
splits into a  -invariant vector field
-invariant vector field 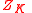 on
on  , called the Kosmann vector field associated with
, called the Kosmann vector field associated with  , and a transverse vector field
, and a transverse vector field  .
.In particular, for a generic vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
 on the base manifold
on the base manifold  , it follows that the restriction
, it follows that the restriction 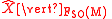 to
to 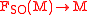 of its natural lift
of its natural lift  onto
onto  splits into a
splits into a  -invariant vector field
-invariant vector field 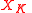 on
on 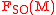 , called the Kosmann lift of
, called the Kosmann lift of  , and a transverse vector field
, and a transverse vector field 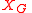 called the von Göden lift of
called the von Göden lift of 
See also
- Frame bundleFrame bundleIn mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
- Orthonormal frame bundle
- Principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
- Spin bundle
- Connection (mathematics)Connection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- G-structureG-structureIn differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
- Spin manifold
- Spin structureSpin structureIn differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....

