Matter collineation
Encyclopedia
A matter collineation is a vector field
that satisfies the condition,
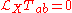
where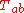
are the energy-momentum tensor components. The intimate relation between geometry and physics may be highlighted here, as the vector field 
is regarded as preserving certain physical quantities along the flow lines of 
, this being true for any two observers. In connection with this, it may be shown that every Killing vector field is a matter collineation (by the Einstein field equations
(EFE), with or without cosmological constant
). Thus, given a solution of the EFE, a vector field that preserves the metric necessarily preserves the corresponding energy-momentum tensor. When the energy-momentum tensor represents a perfect fluid, every Killing vector field
preserves the energy density, pressure and the fluid flow vector field. When the energy-momentum tensor represents an electromagnetic field
, a Killing vector field does not necessarily preserve the electric and magnetic fields.
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
that satisfies the condition,
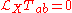
where
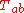are the energy-momentum tensor components. The intimate relation between geometry and physics may be highlighted here, as the vector field is regarded as preserving certain physical quantities along the flow lines of , this being true for any two observers. In connection with this, it may be shown that every Killing vector field is a matter collineation (by the Einstein field equationsEinstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
(EFE), with or without cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
). Thus, given a solution of the EFE, a vector field that preserves the metric necessarily preserves the corresponding energy-momentum tensor. When the energy-momentum tensor represents a perfect fluid, every Killing vector field
Killing vector field
In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
preserves the energy density, pressure and the fluid flow vector field. When the energy-momentum tensor represents an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
, a Killing vector field does not necessarily preserve the electric and magnetic fields.
See also
- Affine vector fieldAffine vector fieldAn affine vector field is a projective vector field preserving geodesics and preserving the affine parameter...
- Conformal vector field
- Curvature collineation
- Homothetic vector field
- Spacetime symmetriesSpacetime symmetriesSpacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...