
Elongated pentagonal cupola
Encyclopedia
In geometry
, the elongated pentagonal cupola is one of the Johnson solid
s (J20). As the name suggests, it can be constructed by elongating a pentagonal cupola
(J5) by attaching a decagonal prism
to its base. The solid can also be seen as an elongated pentagonal orthobicupola
(J38) with its "lid" (another pentagonal cupola
) removed.
The 92 Johnson solids were named and described by Norman Johnson in 1966.
e for volume
and surface area
can be used if all faces
are regular
, with edge length a:
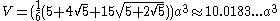

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the elongated pentagonal cupola is one of the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s (J20). As the name suggests, it can be constructed by elongating a pentagonal cupola
Pentagonal cupola
In geometry, the pentagonal cupola is one of the Johnson solids . It can be obtained as a slice of the rhombicosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966....
(J5) by attaching a decagonal prism
Decagonal prism
In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron....
to its base. The solid can also be seen as an elongated pentagonal orthobicupola
Elongated pentagonal orthobicupola
In geometry, the elongated pentagonal orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal orthobicupola by inserting a decagonal prism between its two congruent halves...
(J38) with its "lid" (another pentagonal cupola
Pentagonal cupola
In geometry, the pentagonal cupola is one of the Johnson solids . It can be obtained as a slice of the rhombicosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966....
) removed.
The 92 Johnson solids were named and described by Norman Johnson in 1966.
Formulae
The following formulaFormula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
e for volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
can be used if all faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
are regular
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
, with edge length a:
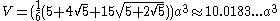

Dual polyhedron
The dual of the elongated pentagonal cupola has 25 faces: 10 isoceles triangles, 5 kites, 10 quadrilaterals.| Dual elongated pentagonal cupola | Net of dual |
|---|---|

