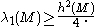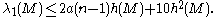Cheeger constant
Encyclopedia
In Riemannian geometry
, the Cheeger isoperimetric constant of a compact
Riemannian manifold
M is a positive real number h(M) defined in terms of the minimal area
of a hypersurface
that divides M into two disjoint pieces of equal volume
. In 1970, Jeff Cheeger
proved an inequality that related the first nontrivial eigenvalue of the Laplace-Beltrami operator
on M to h(M). This proved to be a very influential idea in Riemannian geometry and global analysis and inspired an analogous theory for graph
s.
Riemannian manifold. Let V(A) denote the volume of an n-dimensional submanifold A and S(E) denote the n−1-dimensional volume of a submanifold E (commonly called "area" in this context). The Cheeger isoperimetric constant of M is defined to be
where the infimum
is taken over all smooth n−1-dimensional submanifolds E of M which divide it into two disjoint submanifolds A and B. Isoperimetric constant may be defined more generally for noncompact Riemannian manifolds of finite volume.
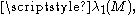 the smallest positive eigenvalue of the Laplacian on M, are related by the following fundamental inequality proved by Jeff Cheeger:
the smallest positive eigenvalue of the Laplacian on M, are related by the following fundamental inequality proved by Jeff Cheeger:
This inequality is optimal in the following sense: for any h > 0, natural number k and ε > 0, there exists a two-dimensional Riemannian manifold M with the isoperimetric constant h(M) = h and such that the kth eigenvalue of the Laplacian is within ε from the Cheeger bound (Buser, 1978).
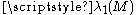 in terms of the isoperimetric constant h(M). Let M be an n-dimensional closed Riemannian manifold whose Ricci curvature
in terms of the isoperimetric constant h(M). Let M be an n-dimensional closed Riemannian manifold whose Ricci curvature
is bounded below by −(n−1)a2, where a ≥ 0. Then
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the Cheeger isoperimetric constant of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M is a positive real number h(M) defined in terms of the minimal area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
that divides M into two disjoint pieces of equal volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
. In 1970, Jeff Cheeger
Jeff Cheeger
Jeff Cheeger , is a mathematician. Cheeger is professor at the Courant Institute of Mathematical Sciences at New York University in New York City. His main interests are differential geometry and its applications to topology and analysis.-Biography:He graduated from Harvard University with a B.A....
proved an inequality that related the first nontrivial eigenvalue of the Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
on M to h(M). This proved to be a very influential idea in Riemannian geometry and global analysis and inspired an analogous theory for graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s.
Definition
Let M be an n-dimensional closedClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
Riemannian manifold. Let V(A) denote the volume of an n-dimensional submanifold A and S(E) denote the n−1-dimensional volume of a submanifold E (commonly called "area" in this context). The Cheeger isoperimetric constant of M is defined to be
where the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
is taken over all smooth n−1-dimensional submanifolds E of M which divide it into two disjoint submanifolds A and B. Isoperimetric constant may be defined more generally for noncompact Riemannian manifolds of finite volume.
Cheeger's inequality
The Cheeger constant h(M) and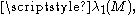 the smallest positive eigenvalue of the Laplacian on M, are related by the following fundamental inequality proved by Jeff Cheeger:
the smallest positive eigenvalue of the Laplacian on M, are related by the following fundamental inequality proved by Jeff Cheeger:This inequality is optimal in the following sense: for any h > 0, natural number k and ε > 0, there exists a two-dimensional Riemannian manifold M with the isoperimetric constant h(M) = h and such that the kth eigenvalue of the Laplacian is within ε from the Cheeger bound (Buser, 1978).
Buser's inequality
Peter Buser proved an upper bound for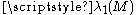 in terms of the isoperimetric constant h(M). Let M be an n-dimensional closed Riemannian manifold whose Ricci curvature
in terms of the isoperimetric constant h(M). Let M be an n-dimensional closed Riemannian manifold whose Ricci curvatureRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
is bounded below by −(n−1)a2, where a ≥ 0. Then