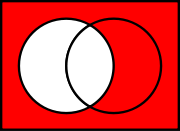
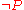Sheffer stroke
Encyclopedia
In Boolean functions and propositional calculus
, the Sheffer stroke, named after Henry M. Sheffer
, written "|" (see vertical bar
, not to be confused with "||" which is often used to represent disjunction
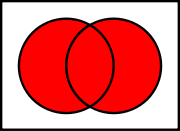
), "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction
operation, expressed in ordinary language as "not both". It is also called the alternative denial, since it says in effect that at least one of its operands is false. In Boolean algebra and digital electronics it is known as the NAND operation ("not and").
Like its dual
, the NOR operator
(a.k.a. the Peirce arrow or Quine
dagger), NAND can be used by itself, without any other logical operator, to constitute a logical formal system
(making NAND functionally complete). This property makes the NAND gate crucial to modern digital electronics, including its use in NAND flash memory and computer processor design.
s, typically the values of two proposition
s, that produces a value of false if and only if both of its operands are true. In other words, it produces a value of true if and only if at least one of its operands is false.
of A NAND B (also written as A | B, Dpq, or A ↑ B) is as follows:
, who provided (Sheffer 1913) an axiomatization of Boolean algebras using the stroke, and proved its equivalence to a standard formulation thereof by Huntington
employing the familiar operators of propositional logic (and
, or
, not
). Because of self-duality
of Boolean algebras, Sheffer's axioms are equally valid for either of the NAND or NOR operations in place of the stroke. Sheffer interpreted the stroke as a sign for non-disjunction (NOR) in his paper, mentioning non-conjunction only in a footnote and without a special sign for it. It was Jean Nicod who first used the stroke as a sign for non-conjunction (NAND) in a paper of 1917 and which has since become current practice.
Charles Sanders Peirce (1880) had discovered the functional completeness of NAND or NOR more than 30 years earlier, using the term ampheck (for ‘cutting both ways’), but he never published his finding.
, monotonicity, self-duality. (An operator is truth- (falsity-) preserving if its value is truth (falsity) whenever all of its arguments are truth (falsity).) Therefore {NAND} is a functionally complete set.
This can also be realized as follows: All three elements of the functionally-complete set {AND, OR, NOT} can be constructed using only NAND. Thus the set {NAND} must be functionally complete as well.
 is the negation of the conjunction:
is the negation of the conjunction:
Expressed in terms of NAND , the usual operators of propositional logic are:
, the usual operators of propositional logic are:
based entirely on the Sheffer stroke, yet having the functional expressiveness of the propositional logic:
( | )
The Sheffer stroke commutes but does not associate (e.g., (T|T)|F = T, but T|(T|F) = F). Hence any formal system including the Sheffer stroke must also include a means of indicating grouping. We shall employ '(' and ')' to this effect.
We also write p, q, r, … instead of p0, p1, p2.
(wff), called an atom.
Construction Rule II: If X and Y are wffs, then (X|Y) is a wff.
Closure Rule: Any formulae which cannot be constructed by means of the first two Construction Rules are not wffs.
The letters U, V, W, X, and Y are metavariables standing for wffs.
A decision procedure for determining whether a formula is well-formed goes as follows: "deconstruct" the formula by applying the Construction Rules backwards, thereby breaking the formula into smaller subformulae. Then repeat this recursive deconstruction process to each of the subformulae. Eventually the formula should be reduced to its atoms, but if some subformula cannot be so reduced, then the formula is not a wff.
are axioms. Instances of), U W
W
are inference rules.
The notation can be simplified further, by letting
for any U. This simplification causes the need to change some rules:
The result is a parenthetical version of the Peirce existential graph
s.
Another way to simplify the notation is to eliminate parenthesis by using Polish Notation
. For example, the earlier examples with only parenthesis could be rewritten using only strokes as follows
This follows the same rules as the parenthesis version, with opening parenthesis replaced with a Sheffer stroke and the (redundant) closing parenthesis removed.
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
, the Sheffer stroke, named after Henry M. Sheffer
Henry M. Sheffer
Henry Maurice Sheffer was an American logician.Sheffer was a Polish Jew born in the western Ukraine, who immigrated to the USA in 1892 with his parents and six siblings. He studied at the Boston Latin School before entering Harvard University, learning logic from Josiah Royce, and completing his...
, written "|" (see vertical bar
Vertical bar
The vertical bar is a character with various uses in mathematics, where it can be used to represent absolute value, among others; in computing and programming and in general typography, as a divider not unlike the interpunct...
, not to be confused with "||" which is often used to represent disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
), "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
operation, expressed in ordinary language as "not both". It is also called the alternative denial, since it says in effect that at least one of its operands is false. In Boolean algebra and digital electronics it is known as the NAND operation ("not and").
Like its dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
, the NOR operator
Logical NOR
In boolean logic, logical nor or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form is true precisely when neither p nor q is true—i.e. when both of p and q are false...
(a.k.a. the Peirce arrow or Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
dagger), NAND can be used by itself, without any other logical operator, to constitute a logical formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
(making NAND functionally complete). This property makes the NAND gate crucial to modern digital electronics, including its use in NAND flash memory and computer processor design.
Definition
The NAND operation is a logical operation on two logical valueLogical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of false if and only if both of its operands are true. In other words, it produces a value of true if and only if at least one of its operands is false.
Truth table
The truth tableTruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
of A NAND B (also written as A | B, Dpq, or A ↑ B) is as follows:
| INPUT | OUTPUT | |
| A | B | A NAND B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
History
The stroke is named after Henry M. ShefferHenry M. Sheffer
Henry Maurice Sheffer was an American logician.Sheffer was a Polish Jew born in the western Ukraine, who immigrated to the USA in 1892 with his parents and six siblings. He studied at the Boston Latin School before entering Harvard University, learning logic from Josiah Royce, and completing his...
, who provided (Sheffer 1913) an axiomatization of Boolean algebras using the stroke, and proved its equivalence to a standard formulation thereof by Huntington
Edward Vermilye Huntington
Edward Vermilye Huntington was an American mathematician....
employing the familiar operators of propositional logic (and
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, or
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
, not
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
). Because of self-duality
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
of Boolean algebras, Sheffer's axioms are equally valid for either of the NAND or NOR operations in place of the stroke. Sheffer interpreted the stroke as a sign for non-disjunction (NOR) in his paper, mentioning non-conjunction only in a footnote and without a special sign for it. It was Jean Nicod who first used the stroke as a sign for non-conjunction (NAND) in a paper of 1917 and which has since become current practice.
Charles Sanders Peirce (1880) had discovered the functional completeness of NAND or NOR more than 30 years earlier, using the term ampheck (for ‘cutting both ways’), but he never published his finding.
Properties
NAND does not possess any of the following five properties, each of which is required to be absent from, and the absence of all of which is sufficient for, at least one member of a set of functionally complete operators: truth-preservation, falsity-preservation, linearityAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
, monotonicity, self-duality. (An operator is truth- (falsity-) preserving if its value is truth (falsity) whenever all of its arguments are truth (falsity).) Therefore {NAND} is a functionally complete set.
This can also be realized as follows: All three elements of the functionally-complete set {AND, OR, NOT} can be constructed using only NAND. Thus the set {NAND} must be functionally complete as well.
Introduction, elimination, and equivalencies
The Sheffer stroke is the negation of the conjunction:
is the negation of the conjunction: |
 |
 |
 |
 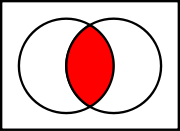 |
Expressed in terms of NAND
 , the usual operators of propositional logic are:
, the usual operators of propositional logic are:EWLINE
|
EWLINE
|
|||||||||||||||||||||||||
EWLINE
|
EWLINE
|
Formal system based on the Sheffer stroke
The following is an example of a formal systemFormal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
based entirely on the Sheffer stroke, yet having the functional expressiveness of the propositional logic:
Symbols
pn for natural numbers n( | )
The Sheffer stroke commutes but does not associate (e.g., (T|T)|F = T, but T|(T|F) = F). Hence any formal system including the Sheffer stroke must also include a means of indicating grouping. We shall employ '(' and ')' to this effect.
We also write p, q, r, … instead of p0, p1, p2.
Syntax
Construction Rule I: For each natural number n, the symbol pn is a well-formed formulaWell-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
(wff), called an atom.
Construction Rule II: If X and Y are wffs, then (X|Y) is a wff.
Closure Rule: Any formulae which cannot be constructed by means of the first two Construction Rules are not wffs.
The letters U, V, W, X, and Y are metavariables standing for wffs.
A decision procedure for determining whether a formula is well-formed goes as follows: "deconstruct" the formula by applying the Construction Rules backwards, thereby breaking the formula into smaller subformulae. Then repeat this recursive deconstruction process to each of the subformulae. Eventually the formula should be reduced to its atoms, but if some subformula cannot be so reduced, then the formula is not a wff.
Calculus
All wffs of the form)|((Y|(Y|Y))|((X|V)|((U|X)|(U|X)))))are axioms. Instances of), U
 W
Ware inference rules.
Simplification
Since the only connective of this logic is |, the symbol | could be discarded altogether, leaving only the parentheses to group the letters. A pair of parentheses must always enclose a pair of wffs. Examples of theorems in this simplified notation are- (p(p(q(q((pq)(pq)))))),
- (p(p((qq)(pp)))).
The notation can be simplified further, by letting
- (U) := (UU)
- ((U))
 U
U
for any U. This simplification causes the need to change some rules:
- More than two letters are allowed within parentheses.
- Letters or wffs within parentheses are allowed to commute.
- Repeated letters or wffs within a same set of parentheses can be eliminated.
The result is a parenthetical version of the Peirce existential graph
Existential graph
An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914.-The graphs:...
s.
Another way to simplify the notation is to eliminate parenthesis by using Polish Notation
Polish notation
Polish notation, also known as prefix notation, is a form of notation for logic, arithmetic, and algebra. Its distinguishing feature is that it places operators to the left of their operands. If the arity of the operators is fixed, the result is a syntax lacking parentheses or other brackets that...
. For example, the earlier examples with only parenthesis could be rewritten using only strokes as follows
- (p(p(q(q((pq)(pq)))))) becomes
- |p|p|q|q||pq|pq, and
- (p(p((qq)(pp)))) becomes,
- |p|p||qq|pp.
This follows the same rules as the parenthesis version, with opening parenthesis replaced with a Sheffer stroke and the (redundant) closing parenthesis removed.
External links
- http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand.html
- implementations of 2 and 4-input NAND gates
- Proofs of some axioms by Stroke function by Yasuo Setô @ Project Euclid