
Minimal logic
Encyclopedia
Minimal logic, or minimal calculus, is a symbolic logic
system originally developed by Ingebrigt Johansson
. It is a variant of intuitionistic logic
that rejects not only the classical
law of excluded middle
(as intuitionistic logic does), but also the principle of explosion
(ex falso quodlibet).
Just like intuitionistic logic, minimal logic can be formulated in a language using →, ∧, ∨, ⊥ (implication, conjunction
, disjunction
and falsum
) as the basic connectives
, treating ¬A as an abbreviation for (A → ⊥). In this language it is axiomatized by the positive fragment (i.e., formulas using only →, ∧, ∨) of intuitionistic logic, with no additional axioms or rules about ⊥. Thus minimal logic is a subsystem of intuitionistic logic, and it is strictly weaker as it does not derive the ex falso quodlibet principle (however, it derives its special case
(however, it derives its special case 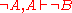 ).
).
Adding the ex falso axiom to minimal logic results in intuitionistic logic, and adding the double negation law
to minimal logic results in intuitionistic logic, and adding the double negation law  to minimal logic results in classical logic.
to minimal logic results in classical logic.
Minimal logic is closely related to simply typed lambda calculus
via the Curry-Howard isomorphism, ie. the typing derivations of simply typed lambda terms are isomorphic to natural deduction
proofs in minimal logic.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
system originally developed by Ingebrigt Johansson
Ingebrigt Johansson
Ingebrigt Johansson was a Norwegian mathematician. He developed the symbolic logic system known as minimal logic.- External links :*...
. It is a variant of intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
that rejects not only the classical
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
(as intuitionistic logic does), but also the principle of explosion
Principle of explosion
The principle of explosion, or the principle of Pseudo-Scotus, is the law of classical logic and intuitionistic and similar systems of logic, according to which any statement can be proven from a contradiction...
(ex falso quodlibet).
Just like intuitionistic logic, minimal logic can be formulated in a language using →, ∧, ∨, ⊥ (implication, conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
and falsum
Falsum
The up tack is a constant symbol used to represent:* Bottom element in lattice theory.* The bottom type in type theory.* A logical constant denoting contradiction in logic.It appears as the upside down tee symbol....
) as the basic connectives
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
, treating ¬A as an abbreviation for (A → ⊥). In this language it is axiomatized by the positive fragment (i.e., formulas using only →, ∧, ∨) of intuitionistic logic, with no additional axioms or rules about ⊥. Thus minimal logic is a subsystem of intuitionistic logic, and it is strictly weaker as it does not derive the ex falso quodlibet principle
 (however, it derives its special case
(however, it derives its special case 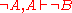 ).
).Adding the ex falso axiom
 to minimal logic results in intuitionistic logic, and adding the double negation law
to minimal logic results in intuitionistic logic, and adding the double negation law  to minimal logic results in classical logic.
to minimal logic results in classical logic.Minimal logic is closely related to simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
via the Curry-Howard isomorphism, ie. the typing derivations of simply typed lambda terms are isomorphic to natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
proofs in minimal logic.

