Ideal (set theory)
Encyclopedia
In the mathematical field of set theory
, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset
of an element of the ideal must also be in the ideal (this codifies the idea that an ideal is a notion of smallness), and the union
of any two elements of the ideal must also be in the ideal.
More formally, given a set X, an ideal on X is a nonempty subset I of the powerset of X, such that:
Some authors add a third condition that X itself is not in I; ideals with this extra property are called proper ideals.
Ideals in the set-theoretic sense are exactly ideals in the order-theoretic sense
, where the relevant order is set inclusion. Also, they are exactly ideals in the ring-theoretic sense
on the Boolean ring
formed by the powerset of the underlying set.
X×Y, as follows: For any subset A ⊆ X×Y,
That is, a set is negligible in the product ideal if only a negligible collection of x-coordinates correspond to a non-negligible slice of A in the y-direction. (Perhaps clearer: A set is positive in the product ideal if positively many x-coordinates correspond to positive slices.)
An ideal I on a set X induces an equivalence relation
on P(X), the powerset of X, considering A and B to be equivalent (for A, B subsets of X) if and only if the symmetric difference
of A and B is an element of I. The quotient of P(X) by this equivalence relation is a Boolean algebra, denoted P(X) / I (read "P of X mod I").
To every ideal there is a corresponding filter, called its dual filter. If I is an ideal on X, then the dual filter of I is the collection of all sets X \ A, where A is an element of I. (Here X \ A denotes the relative complement of A in X; that is, the collection of all elements of X that are not in A.)
φ : X \ A → Y \ B, such that for any subset C of X, C is in I if and only if the image
of C under φ is in J.
If I and J are Rudin–Keisler isomorphic, then P(X) / I and P(Y) / J are isomorphic as Boolean algebras. Isomorphisms of quotient Boolean algebras induced by Rudin–Keisler isomorphisms of ideals are called trivial isomorphisms.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of an element of the ideal must also be in the ideal (this codifies the idea that an ideal is a notion of smallness), and the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of any two elements of the ideal must also be in the ideal.
More formally, given a set X, an ideal on X is a nonempty subset I of the powerset of X, such that:
- if A ∈ I and B ⊆ A, then also B ∈ I, and
- if A,B ∈ I, then A∪B ∈ I.
Some authors add a third condition that X itself is not in I; ideals with this extra property are called proper ideals.
Ideals in the set-theoretic sense are exactly ideals in the order-theoretic sense
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
, where the relevant order is set inclusion. Also, they are exactly ideals in the ring-theoretic sense
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
on the Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
formed by the powerset of the underlying set.
Terminology
An element of an ideal I is said to be I-null or I-negligible, or simply null or negligible if the ideal I is understood from context. If I is an ideal on X, then a subset of X is said to be I-positive (or just positive) if it is not an element of I. The collection of all I-positive subsets of X is denoted I+.General examples
- For any set X and any arbitrarily chosen subset B ⊆ X, the subsets of B form an ideal on X. For finite X, all ideals are of this form.
- The finite subsets of any set X form an ideal on X.
- For any measure space, sets of measure zero.
- For any measure space, sets of finite measure. This encompasses finite subsets (using counting measureCounting measureIn mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
) and small sets below.
Ideals on the natural numbers
- The ideal of all finite sets of natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is denoted Fin. - The summable ideal on the natural numbers, denoted
, is the collection of all sets A of natural numbers such that the sum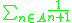 
is finite. See small set. - The ideal of asymptotically zero-density sets on the natural numbers, denoted
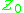, is the collection of all sets A of natural numbers such that the fraction of natural numbers less than n that belong to A, tends to zero as n tends to infinity. (That is, the asymptotic density of A is zero.)
Ideals on the real numbers
- The measure ideal is the collection of all sets A of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s such that the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of A is zero. - The meager ideal is the collection of all meager sets of real numbers.
Ideals on other sets
- If λ is an ordinal numberOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
of uncountable cofinalityCofinalityIn mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
, the nonstationary ideal on λ is the collection of all subsets of λ that are not stationary setStationary setIn mathematics, particularly in set theory and model theory, there are at least three notions of stationary set:-Classical notion:If \kappa \, is a cardinal of uncountable cofinality, S \subseteq \kappa \,, and S \, intersects every club set in \kappa \,, then S \, is called a stationary set....
s. This ideal has been studied extensively by W. Hugh WoodinW. Hugh WoodinWilliam Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
.
Operations on ideals
Given ideals I and J on underlying sets X and Y respectively, one forms the product I×J on the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X×Y, as follows: For any subset A ⊆ X×Y,
That is, a set is negligible in the product ideal if only a negligible collection of x-coordinates correspond to a non-negligible slice of A in the y-direction. (Perhaps clearer: A set is positive in the product ideal if positively many x-coordinates correspond to positive slices.)
An ideal I on a set X induces an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on P(X), the powerset of X, considering A and B to be equivalent (for A, B subsets of X) if and only if the symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
of A and B is an element of I. The quotient of P(X) by this equivalence relation is a Boolean algebra, denoted P(X) / I (read "P of X mod I").
To every ideal there is a corresponding filter, called its dual filter. If I is an ideal on X, then the dual filter of I is the collection of all sets X \ A, where A is an element of I. (Here X \ A denotes the relative complement of A in X; that is, the collection of all elements of X that are not in A.)
Relationships among ideals
If I and J are ideals on X and Y respectively, I and J are Rudin–Keisler isomorphic if they are the same ideal except for renaming of the elements of their underlying sets (ignoring negligible sets). More formally, the requirement is that there be sets A and B, elements of I and J respectively, and a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
φ : X \ A → Y \ B, such that for any subset C of X, C is in I if and only if the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of C under φ is in J.
If I and J are Rudin–Keisler isomorphic, then P(X) / I and P(Y) / J are isomorphic as Boolean algebras. Isomorphisms of quotient Boolean algebras induced by Rudin–Keisler isomorphisms of ideals are called trivial isomorphisms.