Hyperarithmetical theory
Encyclopedia
In recursion theory
, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic
and with weak systems of set theory such as Kripke–Platek set theory
. It is an important tool in effective descriptive set theory
.
s known as hyperarithmetic sets. There are three equivalent ways of defining this class of sets; the study of the relationships between these different definitions is one motivation for the study of hyperarithmetical theory.
.
A set of natural numbers is classified at level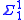
of this hierarchy if it is definable by a formula of second-order arithmetic
with only existential set quantifiers and no other set quantifiers. A set is classified at level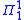
of the analytical hierarchy if it is definable by a formula of second-order arithmetic with only universal set quantifiers and no other set quantifiers. A set is 
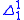if it is both 
and 
. The hyperarithmetical sets are exactly the 
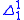sets.
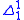does not directly depend on computability results. A second, equivalent, definition shows that the hyperarithmetical sets can be defined using infinitely iterated Turing jump
s. This second definition also shows that the hyperarithmetical sets can be classified into a hierarchy extending the arithmetical hierarchy
; the hyperarithmetical sets are exactly the sets that are assigned a rank in this hierarchy.
Each level of the hyperarithmetical hierarchy corresponds to a countable ordinal number
(ordinal), but not all countable ordinals correspond to a level of the hierarchy. The ordinals used by the hierarchy are those with an ordinal notation
, which is a concrete, effective description of the ordinal.
An ordinal notation is an effective description of a countable ordinal by a natural number. A system of ordinal notations is required in order to define the hyperarithmetic hierarchy. The fundamental property an ordinal notation must have is that it describes the ordinal in terms of small ordinals in an effective way. The following inductive definition is typical; it uses a pairing function
.
There are only countably many ordinal notations, since each notation is a natural number; thus there is a countable ordinal which is the supremum of all ordinals that have a notation. This ordinal is known as the Church-Kleene ordinal and is denoted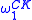
. Note that this ordinal is still countable, the symbol being only an analogy with the first uncountable ordinal, 
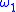. The set of all natural numbers that are ordinal notations is denoted 
and called Kleene's 
.
Ordinal notations are used to define iterated Turing jumps. These are sets of natural numbers denoted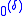
for each 
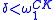. Suppose that δ has notation e. The set 
is defined using e as follows.
Although the construction of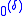
depends on having a fixed notation for δ, and each infinite ordinal has many notations, a theorem of Spector shows that the Turing degree
of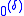
depends only on δ, not on the particular notation used, and thus 
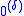is well defined up to Turing degree.
The hyperarithmetical hierarchy is defined from these iterated Turing jumps. A set X of natural numbers is classified at level δ of the hyperarithmetical hierarchy, for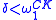
, if X is Turing reducible
to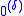
. There will always be a least such δ if there is any; it is this least δ that measures the level of uncomputability of X.
computable functionals. The type-2 functional
is defined by the following rules: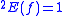
if there is an i such that f(i) > 0,
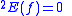if there is no i such that f(i) > 0.
Using a precise definition of computability relative to a type-2 functional, Kleene showed that a set of natural numbers is hyperarithmetical if and only if it is computable relative to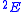
.
is hyperarithmetical, but there are many other hyperarithmetical sets. One example of a hyperarithmetical, nonarithmetical set is the set T of Gödel numbers of formulas of Peano arithmetic
that are true in the standard natural numbers
. The set T is Turing equivalent
to the set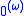
, and so is not high in the hyperarithmetical hierarchy, although it is not arithmetically definable by Tarski's indefinability theorem
.
Completeness results are also fundamental to the theory. A set of natural numbers is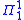
complete if it is at level 
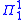of the analytical hierarchy
and every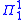
set of natural numbers is many-one reducible
to it. The definition of a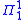
complete subset of Baire space (
) is similar. Several sets associated with hyperarithmetic theory are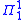 
complete:
Results known as
bounding follow from these completeness results. For any 
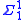set S of ordinal notations, there is an 
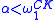such that every element of S is a notation for an ordinal less than 
. For any subset T of Baire space consisting only of characteristic functions of well orderings, there is an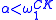 
such that each ordinal represented in T is less than 
.
can be relativized to a set X of natural numbers: in the definition of an ordinal notation, the clause for limit ordinals is changed so that the computable enumeration of a sequence of ordinal notations is allowed to use X as an oracle. The set of numbers that are ordinal notations relative to X is denoted 
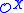. The supremum of ordinals represented in 
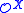is denoted 
; this is a countable ordinal no smaller than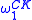 
.
The definition of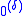
can also be relativized to an arbitrary set 
of natural numbers. The only change in the definition is that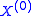 
is defined to be X rather than the empty set, so that 
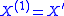is the Turing jump of X, and so on. Rather than terminating at 
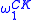the hierarchy relative to X runs through all ordinals less than 
.
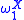The relativized hyperarithmetical hierarchy is used to define hyperarithmetical reducibility. Given sets X and Y, we say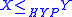
if and only if there is a 
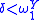such that X is Turing reducible to 
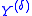. If 
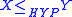and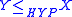 
then the notation 
is used to indicate X and Y are hyperarithmetically equivalent. This is a coarser equivalence relation than Turing equivalence
; for example, every set of natural numbers is hyperarithmetically equivalent to its Turing jump
but not Turing equivalent to its Turing jump. The equivalence classes of hyperarithmetical equivalence are known as hyperdegrees.
The function that takes a set X to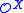
is known as the hyperjump by analogy with the Turing jump. Many properties of the hyperjump and hyperdegrees have been established. In particular, it is known that Post's problem for hyperdegrees has a positive answer: for every set X of natural numbers there is a set Y of natural numbers such that 
.
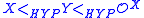, which is the study of definable subsets of admissible ordinal
s. Hyperarithmetical theory is the special case in which α is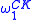
.
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
and with weak systems of set theory such as Kripke–Platek set theory
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
. It is an important tool in effective descriptive set theory
Effective descriptive set theory
Effective descriptive set theory is the branch of descriptive set theory dealing with sets of reals having lightface definitions; that is, definitions that do not require an arbitrary real parameter. Thus effective descriptive set theory combines descriptive set theory with recursion theory....
.
Hyperarithmetical sets
The central focus of hyperarithmetic theory are certain sets of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s known as hyperarithmetic sets. There are three equivalent ways of defining this class of sets; the study of the relationships between these different definitions is one motivation for the study of hyperarithmetical theory.
Hyperarithmetical sets and definability
The first definition of the hyperarithmetic sets uses the analytical hierarchyAnalytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
.
A set of natural numbers is classified at level
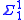of this hierarchy if it is definable by a formula of second-order arithmeticSecond-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
with only existential set quantifiers and no other set quantifiers. A set is classified at level
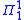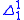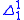of the analytical hierarchy if it is definable by a formula of second-order arithmetic with only universal set quantifiers and no other set quantifiers. A set is if it is both and . The hyperarithmetical sets are exactly the sets.Hyperarithmetical sets and iterated Turing jumps: the hyperarithmetical hierarchy
The definition of hyperarithmetical sets as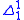 does not directly depend on computability results. A second, equivalent, definition shows that the hyperarithmetical sets can be defined using infinitely iterated Turing jumpTuring jump
In computability theory, the Turing jump or Turing jump operator, named for Alan Turing, is an operation that assigns to each decision problem a successively harder decision problem with the property that is not decidable by an oracle machine with an oracle for .The operator is called a jump...
s. This second definition also shows that the hyperarithmetical sets can be classified into a hierarchy extending the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
; the hyperarithmetical sets are exactly the sets that are assigned a rank in this hierarchy.
Each level of the hyperarithmetical hierarchy corresponds to a countable ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
(ordinal), but not all countable ordinals correspond to a level of the hierarchy. The ordinals used by the hierarchy are those with an ordinal notation
Ordinal notation
In mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....
, which is a concrete, effective description of the ordinal.
An ordinal notation is an effective description of a countable ordinal by a natural number. A system of ordinal notations is required in order to define the hyperarithmetic hierarchy. The fundamental property an ordinal notation must have is that it describes the ordinal in terms of small ordinals in an effective way. The following inductive definition is typical; it uses a pairing function
Pairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
.
- The number 0 is a notation for the ordinal 0.
- If n is a notation for an ordinal λ then
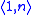is a notation for λ + 1; - Suppose that δ is a limit ordinal. A notation for δ is a number of the form
, where e is the index of a total computable function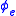 
such that for each n, 
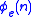is a notation for an ordinal λn less than δ and δ is the supSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the set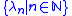
.
There are only countably many ordinal notations, since each notation is a natural number; thus there is a countable ordinal which is the supremum of all ordinals that have a notation. This ordinal is known as the Church-Kleene ordinal and is denoted
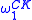. Note that this ordinal is still countable, the symbol being only an analogy with the first uncountable ordinal, 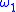. The set of all natural numbers that are ordinal notations is denoted and called Kleene's .Ordinal notations are used to define iterated Turing jumps. These are sets of natural numbers denoted
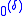for each 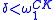. Suppose that δ has notation e. The set is defined using e as follows.
- If δ = 0 then
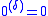is the empty set. - If δ = λ + 1 then
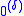is the Turing jump of 
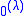. The notations 
and 
are commonly used for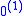 
and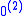 
, respectively. - If δ is a limit ordinal, let
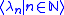be the sequence of ordinals less than δ given by the notation e. The set 
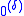is given by the rule 
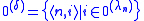. This is the effective join of the sets 
.
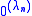Although the construction of
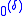depends on having a fixed notation for δ, and each infinite ordinal has many notations, a theorem of Spector shows that the Turing degreeTuring degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
of
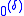depends only on δ, not on the particular notation used, and thus 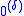is well defined up to Turing degree.The hyperarithmetical hierarchy is defined from these iterated Turing jumps. A set X of natural numbers is classified at level δ of the hyperarithmetical hierarchy, for
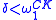, if X is Turing reducibleTuring reduction
In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...
to
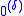. There will always be a least such δ if there is any; it is this least δ that measures the level of uncomputability of X.Hyperarithmetical sets and recursion in higher types
A third characterization of the hyperarithmetical sets, due to Kleene, uses higher-typeType theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
computable functionals. The type-2 functional
is defined by the following rules: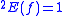 if there is an i such that f(i) > 0, 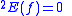if there is no i such that f(i) > 0.Using a precise definition of computability relative to a type-2 functional, Kleene showed that a set of natural numbers is hyperarithmetical if and only if it is computable relative to
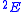.Example: the truth set of arithmetic
Every arithmetical setArithmetical set
In mathematical logic, an arithmetical set is a set of natural numbers that can be defined by a formula of first-order Peano arithmetic...
is hyperarithmetical, but there are many other hyperarithmetical sets. One example of a hyperarithmetical, nonarithmetical set is the set T of Gödel numbers of formulas of Peano arithmetic
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
that are true in the standard natural numbers
. The set T is Turing equivalentTuring reduction
In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...
to the set
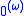, and so is not high in the hyperarithmetical hierarchy, although it is not arithmetically definable by Tarski's indefinability theoremTarski's indefinability theorem
Tarski's undefinability theorem, stated and proved by Alfred Tarski in 1936, is an important limitative result in mathematical logic, the foundations of mathematics, and in formal semantics...
.
Fundamental results
The fundamental results of hyperarithmetic theory show that the three definitions above define the same collection of sets of natural numbers. These equivalences are due to Kleene.Completeness results are also fundamental to the theory. A set of natural numbers is
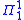complete if it is at level 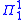of the analytical hierarchyAnalytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
and every
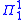set of natural numbers is many-one reducibleMany-one reduction
In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
to it. The definition of a
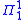complete subset of Baire space () is similar. Several sets associated with hyperarithmetic theory are 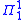complete:
- Kleene's
, the set of natural numbers that are notations for ordinal numbers - The set of natural numbers e such that the computable function
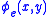computes the characteristic function of a well ordering of the natural numbers. These are the indices of recursive ordinalRecursive ordinalIn mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
s. - The set of elements of Baire space that are the characteristic functions of a well ordering of the natural numbers (using an effective isomorphism
.
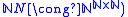Results known as
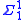bounding follow from these completeness results. For any set S of ordinal notations, there is an 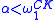such that every element of S is a notation for an ordinal less than . For any subset T of Baire space consisting only of characteristic functions of well orderings, there is an 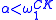such that each ordinal represented in T is less than .Relativized hyperarithmeticity and hyperdegrees
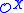The definition of can be relativized to a set X of natural numbers: in the definition of an ordinal notation, the clause for limit ordinals is changed so that the computable enumeration of a sequence of ordinal notations is allowed to use X as an oracle. The set of numbers that are ordinal notations relative to X is denoted . The supremum of ordinals represented in 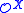is denoted ; this is a countable ordinal no smaller than 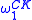.The definition of
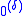can also be relativized to an arbitrary set of natural numbers. The only change in the definition is that 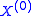is defined to be X rather than the empty set, so that 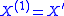is the Turing jump of X, and so on. Rather than terminating at 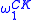the hierarchy relative to X runs through all ordinals less than 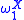.The relativized hyperarithmetical hierarchy is used to define hyperarithmetical reducibility. Given sets X and Y, we say
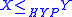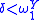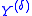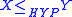if and only if there is a such that X is Turing reducible to . If and 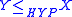then the notation is used to indicate X and Y are hyperarithmetically equivalent. This is a coarser equivalence relation than Turing equivalenceTuring reduction
In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...
; for example, every set of natural numbers is hyperarithmetically equivalent to its Turing jump
Turing jump
In computability theory, the Turing jump or Turing jump operator, named for Alan Turing, is an operation that assigns to each decision problem a successively harder decision problem with the property that is not decidable by an oracle machine with an oracle for .The operator is called a jump...
but not Turing equivalent to its Turing jump. The equivalence classes of hyperarithmetical equivalence are known as hyperdegrees.
The function that takes a set X to
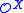is known as the hyperjump by analogy with the Turing jump. Many properties of the hyperjump and hyperdegrees have been established. In particular, it is known that Post's problem for hyperdegrees has a positive answer: for every set X of natural numbers there is a set Y of natural numbers such that 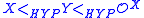.Generalizations
Hyperarithmetical theory is generalized by α-recursion theoryAlpha recursion theory
In recursion theory, α recursion theory is a generalisation of recursion theory to subsets of admissible ordinals \alpha. An admissible ordinal is closed under \Sigma_1 functions. Admissible ordinals are models of Kripke–Platek set theory. In what follows \alpha is considered to be fixed.The...
, which is the study of definable subsets of admissible ordinal
Admissible ordinal
In set theory, an ordinal number α is an admissible ordinal if Lα is an admissible set ; in other words, α is admissible when α is a limit ordinal and Lα⊧Σ0-collection....
s. Hyperarithmetical theory is the special case in which α is
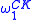.External links
- Descriptive set theory. Notes by David Marker, University of Illinois at Chicago. 2002.
- Mathematical Logic II. Notes by Dag Normann, The University of Oslo. 2005.