
Kripke–Platek set theory
Encyclopedia
The Kripke–Platek axioms of set theory (KP) (icon) are a system of axioms for axiomatic set theory developed by Saul Kripke
and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema
is used.
KP is weaker than Zermelo–Fraenkel set theory
(ZFC). Unlike ZFC, KP does not include the powerset axiom, and KP includes only limited forms of the axiom of separation and axiom of replacement from ZFC. These restrictions on the axioms of KP lead to close connections between KP, generalized recursion theory, and the theory of admissible ordinal
s.
Here, a Σ0, or Π0, or Δ0 formula is one all of whose quantifiers are bounded
. This means any quantification is the form or
or 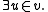 (More generally, we would say that a formula is Σn+1 when it is obtained by adding existential quantifiers in front of a Πn formula, and that it is Πn+1 when it is obtained by adding universal quantifiers in front of a Σn formula: this is related to the arithmetical hierarchy
(More generally, we would say that a formula is Σn+1 when it is obtained by adding existential quantifiers in front of a Πn formula, and that it is Πn+1 when it is obtained by adding universal quantifiers in front of a Σn formula: this is related to the arithmetical hierarchy
but in the context of set theory.)
These axioms differ from ZFC in as much as they exclude the axioms of: infinity, powerset, and choice. Also the axioms of separation and collection here are weaker than the corresponding axioms in ZFC because the formulas φ used in these are limited to bounded quantifiers only.
The axiom of induction here is stronger than the usual axiom of regularity
(which amounts to applying induction to the complement of a set (the class of all sets not in the given set)).
s (a, b) of elements a of A and b of B.
{a} = {a, a} exists by the axiom of pairing. {a, b} exists by the axiom of pairing. Thus (a, b) = { {a}, {a, b} } exists by the axiom of pairing.
If p is intended to stand for (a, b), then a Δ0 formula expressing that is:
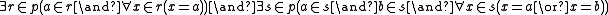 and
and 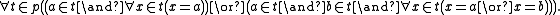
Thus a superset of A×{b} = {(a, b) | a in A} exists by the axiom of collection.
Abbreviate the formula above by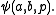 Then
Then 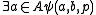 is Δ0. Thus A×{b} itself exists by the axiom of separation.
is Δ0. Thus A×{b} itself exists by the axiom of separation.
If v is intended to stand for A×{b}, then a Δ0 formula expressing that is:
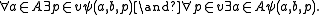
Thus a superset of {A×{b} | b in B} exists by the axiom of collection.
Putting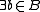 in front of that last formula and we get that the set {A×{b} | b in B} itself exists by the axiom of separation.
in front of that last formula and we get that the set {A×{b} | b in B} itself exists by the axiom of separation.
Finally, A×B = {A×{b} | b in B} exists by the axiom of union. This is what was to be proved.
{A×{b} | b in B} exists by the axiom of union. This is what was to be proved.
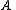 is called admissible
is called admissible
if it is transitive
and is a model
is a model
of Kripke–Platek set theory.
An ordinal number
α is called an admissible ordinal
if Lα
is an admissible set.
The ordinal α is an admissible ordinal if and only if α is a limit ordinal and there does not exist a γ<α for which there is a Σ1(Lα) mapping from γ onto α. If M is a standard model of KP, then the set of ordinals in M is an admissible ordinal.
If Lα is a standard model of KP set theory without the axiom of Σ0-collection, then it is said to be an "amenable set".
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
is used.
KP is weaker than Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
(ZFC). Unlike ZFC, KP does not include the powerset axiom, and KP includes only limited forms of the axiom of separation and axiom of replacement from ZFC. These restrictions on the axioms of KP lead to close connections between KP, generalized recursion theory, and the theory of admissible ordinal
Admissible ordinal
In set theory, an ordinal number α is an admissible ordinal if Lα is an admissible set ; in other words, α is admissible when α is a limit ordinal and Lα⊧Σ0-collection....
s.
The axioms of KP
- Axiom of extensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
: Two sets are the same if and only if they have the same elements. - Axiom of inductionEpsilon-inductionIn mathematics, \in-induction is a variant of transfinite induction, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets...
: If φ(a) is a formula, and if for all sets x it follows from the fact that φ(y) is true for all elements y of x that φ(x) holds, then φ(x) holds for all sets x. - Axiom of empty setAxiom of empty setIn axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
: There exists a set with no members, called the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and denoted {}. (Note: the existence of a member in the universe of discourse, i.e., ∃x(x=x), is implied in certain formulations of first-order logic, in which case the axiom of empty set follows from the axiom of separation, and is thus redundant.) - Axiom of pairingAxiom of pairingIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
: If x, y are sets, then so is {x, y}, a set containing x and y as its only elements. - Axiom of unionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
: For any set x, there is a set y such that the elements of y are precisely the elements of the elements of x. - Axiom of Σ0-separationAxiom schema of predicative separationIn axiomatic set theory, the axiom schema of predicative separation, or of restricted, or Δ0 separation, is a schema of axioms which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset of a set if that subset can...
: Given any set and any Σ0-formula φ(x), there is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the original set containing precisely those elements x for which φ(x) holds. (This is an axiom schema.) - Axiom of Σ0-collection: Given any Σ0-formula φ(x, y), if for every set x there exists a set y such that φ(x, y) holds, then for all sets u there exists a set v such that for every x in u there is a y in v such that φ(x, y) holds.
Here, a Σ0, or Π0, or Δ0 formula is one all of whose quantifiers are bounded
Bounded quantifier
In the study of formal theories in mathematical logic, bounded quantifiers are often added to a language in addition to the standard quantifiers "∀" and "∃". Bounded quantifiers differ from "∀" and "∃" in that bounded quantifiers restrict the range of the quantified variable...
. This means any quantification is the form
 or
or 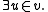 (More generally, we would say that a formula is Σn+1 when it is obtained by adding existential quantifiers in front of a Πn formula, and that it is Πn+1 when it is obtained by adding universal quantifiers in front of a Σn formula: this is related to the arithmetical hierarchy
(More generally, we would say that a formula is Σn+1 when it is obtained by adding existential quantifiers in front of a Πn formula, and that it is Πn+1 when it is obtained by adding universal quantifiers in front of a Σn formula: this is related to the arithmetical hierarchyArithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
but in the context of set theory.)
These axioms differ from ZFC in as much as they exclude the axioms of: infinity, powerset, and choice. Also the axioms of separation and collection here are weaker than the corresponding axioms in ZFC because the formulas φ used in these are limited to bounded quantifiers only.
The axiom of induction here is stronger than the usual axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
(which amounts to applying induction to the complement of a set (the class of all sets not in the given set)).
Proof that Cartesian products exist
Theorem: If A and B are sets, then there is a set A×B which consists of all ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s (a, b) of elements a of A and b of B.
{a} = {a, a} exists by the axiom of pairing. {a, b} exists by the axiom of pairing. Thus (a, b) = { {a}, {a, b} } exists by the axiom of pairing.
If p is intended to stand for (a, b), then a Δ0 formula expressing that is:
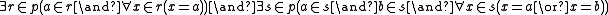 and
and 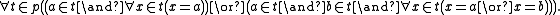
Thus a superset of A×{b} = {(a, b) | a in A} exists by the axiom of collection.
Abbreviate the formula above by
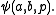 Then
Then 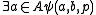 is Δ0. Thus A×{b} itself exists by the axiom of separation.
is Δ0. Thus A×{b} itself exists by the axiom of separation.If v is intended to stand for A×{b}, then a Δ0 formula expressing that is:
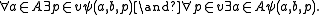
Thus a superset of {A×{b} | b in B} exists by the axiom of collection.
Putting
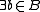 in front of that last formula and we get that the set {A×{b} | b in B} itself exists by the axiom of separation.
in front of that last formula and we get that the set {A×{b} | b in B} itself exists by the axiom of separation.Finally, A×B =
 {A×{b} | b in B} exists by the axiom of union. This is what was to be proved.
{A×{b} | b in B} exists by the axiom of union. This is what was to be proved.Admissible sets
A set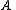 is called admissible
is called admissibleAdmissible set
In set theory, a discipline within mathematics, an admissible set is a transitive set A\, such that \langle A,\in \rangle is a model of Kripke–Platek set theory....
if it is transitive
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
and
 is a model
is a modelModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of Kripke–Platek set theory.
An ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
α is called an admissible ordinal
Admissible ordinal
In set theory, an ordinal number α is an admissible ordinal if Lα is an admissible set ; in other words, α is admissible when α is a limit ordinal and Lα⊧Σ0-collection....
if Lα
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
is an admissible set.
The ordinal α is an admissible ordinal if and only if α is a limit ordinal and there does not exist a γ<α for which there is a Σ1(Lα) mapping from γ onto α. If M is a standard model of KP, then the set of ordinals in M is an admissible ordinal.
If Lα is a standard model of KP set theory without the axiom of Σ0-collection, then it is said to be an "amenable set".
See also
- Constructible universeConstructible universeIn mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
- Admissible ordinalAdmissible ordinalIn set theory, an ordinal number α is an admissible ordinal if Lα is an admissible set ; in other words, α is admissible when α is a limit ordinal and Lα⊧Σ0-collection....
- Kripke–Platek set theory with urelementsKripke–Platek set theory with urelementsThe Kripke–Platek set theory with urelements is an axiom system for set theory with urelements that is considerably weaker than the familiar system ZF.-Preliminaries:...

