Turing reduction
Encyclopedia
In computability theory
, a Turing reduction from a problem A to a problem B, named after Alan Turing
, is a reduction
which solves A, assuming B is already known (Rogers 1967, Soare 1987). It can be understood as an algorithm
that could be used to solve A if it had available to it a subroutine
for solving B. More formally, a Turing reduction is a function computable by an oracle machine
with an oracle for B. Turing reductions can be applied to both decision problem
s and function problem
s.
If a Turing reduction of A to B exists then every algorithm
for B can be used to produce an algorithm for A, by inserting the algorithm for B at each place where the oracle machine computing A queries the oracle for B. However, because the oracle machine may query the oracle a large number of times, the resulting algorithm may require more time asymptotically than either M or the oracle machine, and may require as much space as both together.
The first formal definition of relative computability, then called relative reducibility, was given by Alan Turing
in 1939 in terms of oracle machine
s. Later in 1943 and 1952 Stephen Kleene defined an equivalent concept in terms of recursive function
s. In 1944 Emil Post used the term "Turing reducibility" to refer to the concept.
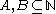of natural numbers, we say 
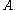is Turing reducible to 
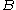and write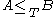
if there is an oracle machine
that computes the characteristic function of A when run with oracle B. In this case, we also say A is B-recursive and B-computable.
If there is an oracle machine that, when run with oracle B, computes a partial function with domain A, then A is said to be B-recursively enumerable
and B-computably enumerable.
We say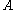
is Turing equivalent to 
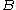and write 
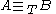if both 
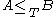and 
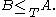The equivalence classes of Turing equivalent sets are called Turing degree
s. The Turing degree of a set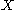
is written 
.
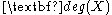Given a set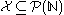
, a set 
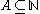is called Turing hard for 
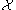if 
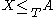for all 
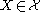. If additionally 
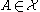then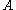 
is called Turing complete for 
.
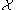in the sense of computational universality. Specifically, a Turing machine is a universal Turing machine
if its halting problem (i.e., the set of inputs for which it eventually halts) is many-one complete
. Thus, a necessary but insufficient condition for a machine to be computationally universal, is that the machine's halting problem be Turing-complete for the set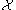
of recursively enumerable sets.
denote the set of input values for which the Turing machine with index e halts. Then the sets 
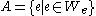and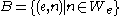 
are Turing equivalent (here 
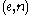denotes an effective pairing function). A reduction showing 
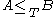can be constructed using the fact that 
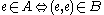. Given a pair 
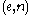, a new index 
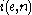can be constructed using the smn theorem such that the program coded by 
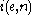ignores its input and merely simulates the computation of the machine with index e on input n.
In particular, the machine with index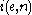
either halts on every input or halts on no input. Thus 
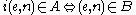holds for all e and n. Because the function i is computable, this shows 
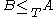. The reductions presented here are not only Turing reductions but many-one reductions, discussed below.
The first way is to limit the number and manner of oracle queries.
The second way to produce a stronger reducibility notion is to limit the computational resources that the program implementing the Turing reduction may use. These limits on the computational complexity
of the reduction are important when studying subrecursive classes such as P
. A set A is polynomial-time reducible
to a set B if there is a Turing reduction of A to B that runs in polynomial time. The concept of log-space reduction
is similar.
Note that while these reductions are stronger in the sense that they provide a finer distinction into equivalence classes, and have more restrictive requirements than Turing reductions, this is because the reductions themselves are less powerful; there may be no way to build a many-one reduction from one set to another even when a Turing reduction for the same sets exists.
in B if A is definable by a formula of Peano arithmetic with B as a parameter. The set A is hyperarithmetical in B if there is a recursive ordinal
α such that A is computable from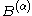
, the α-iterated Turing jump of B. The notion of relative constructibility
is an important reducibility notion in set theory.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, a Turing reduction from a problem A to a problem B, named after Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
, is a reduction
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
which solves A, assuming B is already known (Rogers 1967, Soare 1987). It can be understood as an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that could be used to solve A if it had available to it a subroutine
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
for solving B. More formally, a Turing reduction is a function computable by an oracle machine
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
with an oracle for B. Turing reductions can be applied to both decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s and function problem
Function problem
In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...
s.
If a Turing reduction of A to B exists then every algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for B can be used to produce an algorithm for A, by inserting the algorithm for B at each place where the oracle machine computing A queries the oracle for B. However, because the oracle machine may query the oracle a large number of times, the resulting algorithm may require more time asymptotically than either M or the oracle machine, and may require as much space as both together.
The first formal definition of relative computability, then called relative reducibility, was given by Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
in 1939 in terms of oracle machine
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
s. Later in 1943 and 1952 Stephen Kleene defined an equivalent concept in terms of recursive function
Mu-recursive function
In mathematical logic and computer science, the μ-recursive functions are a class of partial functions from natural numbers to natural numbers which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that...
s. In 1944 Emil Post used the term "Turing reducibility" to refer to the concept.
Definition
Given two sets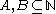 of natural numbers, we say 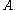is Turing reducible to 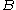and write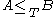if there is an oracle machine
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
that computes the characteristic function of A when run with oracle B. In this case, we also say A is B-recursive and B-computable.
If there is an oracle machine that, when run with oracle B, computes a partial function with domain A, then A is said to be B-recursively enumerable
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
and B-computably enumerable.
We say
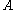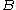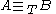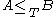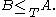is Turing equivalent to and write if both and The equivalence classes of Turing equivalent sets are called Turing degreeTuring degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
s. The Turing degree of a set
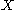is written 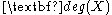.Given a set
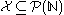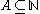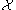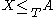, a set is called Turing hard for if for all 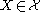. If additionally 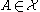then 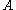is called Turing complete for 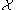.Relation of Turing completeness to computational universality
Turing completeness, as just defined above, corresponds only partially to Turing completenessTuring completeness
In computability theory, a system of data-manipulation rules is said to be Turing complete or computationally universal if and only if it can be used to simulate any single-taped Turing machine and thus in principle any computer. A classic example is the lambda calculus...
in the sense of computational universality. Specifically, a Turing machine is a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
if its halting problem (i.e., the set of inputs for which it eventually halts) is many-one complete
Many-one reduction
In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
. Thus, a necessary but insufficient condition for a machine to be computationally universal, is that the machine's halting problem be Turing-complete for the set
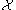of recursively enumerable sets.Example
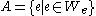Let denote the set of input values for which the Turing machine with index e halts. Then the sets and 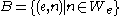are Turing equivalent (here 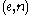denotes an effective pairing function). A reduction showing 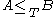can be constructed using the fact that 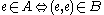. Given a pair 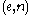, a new index 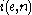can be constructed using the smn theorem such that the program coded by 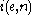ignores its input and merely simulates the computation of the machine with index e on input n.In particular, the machine with index
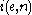either halts on every input or halts on no input. Thus 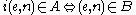holds for all e and n. Because the function i is computable, this shows 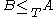. The reductions presented here are not only Turing reductions but many-one reductions, discussed below.Properties
- Every set is Turing equivalent to its complement
- Every computable set is Turing reducible to every other computable set. Because these sets can be computed with no oracle, they can be computed by an oracle machine that ignores the oracle it is given.
- The relation
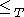is transitive: if 
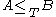and 
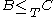then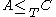 
. Moreover 
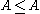holds for every set A, and thus the relation 
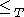is a preorderPreorderIn mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
(it is not a partial order because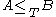
and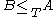 
does not necessarily imply 
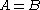). - There are pairs of sets
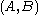such that A is not Turing reducible to B and B is not Turing reducible to A. Thus 
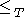is not a linear order. - There are infinite decreasing sequences of sets under
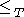. Thus this relation is not well-founded. - Every set is Turing reducible to its own Turing jumpTuring jumpIn computability theory, the Turing jump or Turing jump operator, named for Alan Turing, is an operation that assigns to each decision problem a successively harder decision problem with the property that is not decidable by an oracle machine with an oracle for .The operator is called a jump...
, but the Turing jump of a set is never Turing reducible to the original set.
The use of a reduction
Since every reduction from a set B to a set A has to determine whether a single element is in A in only finitely many steps, it can only make finitely many queries of membership in the set B. When the amount of information about the set B used to compute a single bit of A is discussed, this is made precise by the use function. Formally, the use of a reduction is the function that sends each natural number n to the largest natural number m whose membership in the set B was queried by the reduction while determining the membership of n in A.Stronger reductions
There are two common ways of producing reductions stronger than Turing reducibility.The first way is to limit the number and manner of oracle queries.
- A set A is many-one reducibleMany-one reductionIn computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
to B if there is a total computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
f such that an element n is in A if and only if f(n) is in B. Such a function can be used to generate a Turing reduction (by computing f(n), querying the oracle, and then interpreting the result). - A truth table reductionTruth table reductionIn computability theory, a truth-table reduction is a reduction from one set of natural numbers to another.As a "tool", it is weaker than Turing reduction, since not every Turing reduction between sets can be performed by a truth-table reduction, but every truth-table reduction can be performed by...
or a weak truth table reductionTruth table reductionIn computability theory, a truth-table reduction is a reduction from one set of natural numbers to another.As a "tool", it is weaker than Turing reduction, since not every Turing reduction between sets can be performed by a truth-table reduction, but every truth-table reduction can be performed by...
must present all of its oracle queries at the same time. In a truth table reduction, the reduction also gives a boolean function (a truth table) which, when given the answers to the queries, will produce the final answer of the reduction. In a weak truth table reduction, the reduction uses the oracle answers as a basis for further computation depending on the given answers (but not using the oracle). Equivalently, a weak truth table reduction is one for which the use of the reduction is bounded by a computable function. For this reason, weak truth table reductions are sometimes called "bounded Turing" reductions.
The second way to produce a stronger reducibility notion is to limit the computational resources that the program implementing the Turing reduction may use. These limits on the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of the reduction are important when studying subrecursive classes such as P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
. A set A is polynomial-time reducible
Polynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
to a set B if there is a Turing reduction of A to B that runs in polynomial time. The concept of log-space reduction
Log-space reduction
In computational complexity theory, a log-space reduction is a reduction computable by a deterministic Turing machine using logarithmic space. Conceptually, this means it can keep a constant number of pointers into the input, along with a logarithmic number of fixed-size integers...
is similar.
Note that while these reductions are stronger in the sense that they provide a finer distinction into equivalence classes, and have more restrictive requirements than Turing reductions, this is because the reductions themselves are less powerful; there may be no way to build a many-one reduction from one set to another even when a Turing reduction for the same sets exists.
Weaker reductions
According to the Church-Turing thesis, a Turing reduction is the most general form of an effectively calculable reduction. Nevertheless, weaker reductions are also considered. A set A is said to be arithmeticalArithmetical set
In mathematical logic, an arithmetical set is a set of natural numbers that can be defined by a formula of first-order Peano arithmetic...
in B if A is definable by a formula of Peano arithmetic with B as a parameter. The set A is hyperarithmetical in B if there is a recursive ordinal
Recursive ordinal
In mathematics, specifically set theory, an ordinal \alpha is said to be recursive if there is a recursive binary relation R that well-orders a subset of the natural numbers and the order type of that ordering is \alpha....
α such that A is computable from
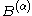, the α-iterated Turing jump of B. The notion of relative constructibilityConstructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
is an important reducibility notion in set theory.