Pairing function
Encyclopedia
In mathematics
a pairing function is a process to uniquely encode two natural number
s into a single natural number.
Any pairing function can be used in set theory
to prove that integer
s and rational number
s have the same cardinality as natural numbers. In theoretical computer science
they are used to encode a function defined on a vector of natural numbers f:Nk → N into a new function g:N → N.
bijection
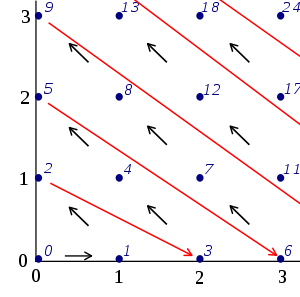 The Cantor pairing function is a pairing function
The Cantor pairing function is a pairing function
defined by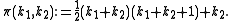
When we apply the pairing function to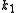 and
and 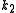 we often denote the resulting number as
we often denote the resulting number as 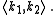
This definition can be inductively generalized to the Cantor tuple function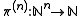
as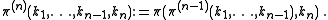
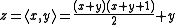
and we want to find x and y. It is helpful to define some intermediate values in the calculation: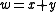
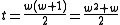
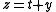
where t is the triangle number
of w. If we solve the quadratic equation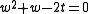
for w as a function of t, we get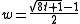
which is a strictly increasing and continuous function when t is non-negative real. Since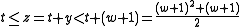
we get that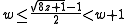
and thus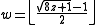 .
.
So to calculate x and y from z, we do: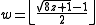
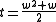

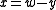 .
.
Since the Cantor pairing function is invertible, it must be one-to-one
and onto
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a pairing function is a process to uniquely encode two natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s into a single natural number.
Any pairing function can be used in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
to prove that integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s have the same cardinality as natural numbers. In theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
they are used to encode a function defined on a vector of natural numbers f:Nk → N into a new function g:N → N.
Definition
A pairing function is a primitive recursivePrimitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
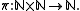
Cantor pairing function

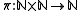
defined by
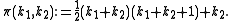
When we apply the pairing function to
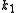 and
and 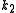 we often denote the resulting number as
we often denote the resulting number as 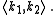
This definition can be inductively generalized to the Cantor tuple function
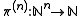
as
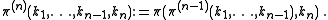
Inverting the Cantor pairing function
Suppose we are given z with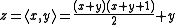
and we want to find x and y. It is helpful to define some intermediate values in the calculation:
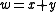
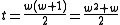
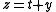
where t is the triangle number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
of w. If we solve the quadratic equation
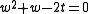
for w as a function of t, we get
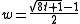
which is a strictly increasing and continuous function when t is non-negative real. Since
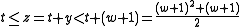
we get that
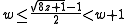
and thus
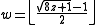 .
.So to calculate x and y from z, we do:
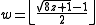
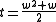

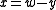 .
.Since the Cantor pairing function is invertible, it must be one-to-one
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and onto
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
.

