
Homeotopy
Encyclopedia
In algebraic topology
, an area of mathematics, a homeotopy group of a topological space
is a homotopy group
of the group of self-homeomorphism
s of that space.
functor
s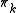 assign to each path-connected topological space
assign to each path-connected topological space  the group
the group 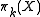 of homotopy classes of continuous maps
of homotopy classes of continuous maps 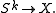
Another construction on a space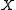 is the group of all self-homeomorphisms
is the group of all self-homeomorphisms
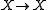 , denoted
, denoted 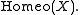 If X is a locally compact, locally connected Hausdorff space
If X is a locally compact, locally connected Hausdorff space
then a fundamental result of R. Arens says that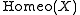 will in fact be a topological group
will in fact be a topological group
under the compact-open topology
.
Under the above assumptions, the homeotopy groups for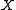 are defined to be:
are defined to be:
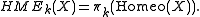
Thus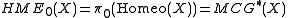 is the extended mapping class group
is the extended mapping class group
for In other words, the extended mapping class group is the set of connected components of
In other words, the extended mapping class group is the set of connected components of  as specified by the functor
as specified by the functor 
 is a closed surface then
is a closed surface then 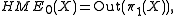 the outer automorphism group
the outer automorphism group
of its fundamental group
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, an area of mathematics, a homeotopy group of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is a homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
of the group of self-homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s of that space.
Definition
The homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s
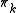 assign to each path-connected topological space
assign to each path-connected topological space  the group
the group 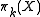 of homotopy classes of continuous maps
of homotopy classes of continuous maps 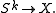
Another construction on a space
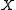 is the group of all self-homeomorphisms
is the group of all self-homeomorphismsHomeomorphism group
In mathematics, particularly topology, the homeomorphism group of a topological space is the group consisting of all homeomorphisms from the space to itself with function composition as the group operation. Homeomorphism groups are very important in the theory of topological spaces and in general...
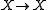 , denoted
, denoted 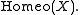 If X is a locally compact, locally connected Hausdorff space
If X is a locally compact, locally connected Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
then a fundamental result of R. Arens says that
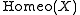 will in fact be a topological group
will in fact be a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
under the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
.
Under the above assumptions, the homeotopy groups for
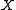 are defined to be:
are defined to be: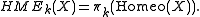
Thus
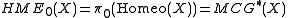 is the extended mapping class group
is the extended mapping class groupMapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
for
 In other words, the extended mapping class group is the set of connected components of
In other words, the extended mapping class group is the set of connected components of  as specified by the functor
as specified by the functor 
Example
According to the Dehn-Nielsen theorem, if is a closed surface then
is a closed surface then 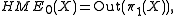 the outer automorphism group
the outer automorphism groupOuter automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
.

