
Homeomorphism group
Encyclopedia
In mathematics
, particularly topology
, the homeomorphism group of a topological space
is the group
consisting of all homeomorphism
s from the space to itself with function composition
as the group operation
. Homeomorphism groups are very important in the theory of topological spaces and in general are examples of automorphism groups. Homeomorphism groups are topological invariants in the sense that the homeomorphism groups of homeomorphic topological spaces are isomorphic as groups
.
of the homeomorphism group of a space on that space. If this action is transitive, then the space is said to be homogeneous
.
, making it into a topological group
.
In the category of topological spaces with homeomorphisms, object groups are exactly homeomorphism groups.
especially, one considers the quotient group
obtained by quotienting out by isotopy, called the mapping class group
:
The MCG can also be interpreted as the 0th homotopy group
,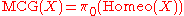 .
.
This yields the short exact sequence:
In some applications, particularly surfaces, the homeomorphism group is studied via this short exact sequence, and by first studying the mapping class group and group of isotopically trivial homeomorphisms, and then (at times) the extension.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the homeomorphism group of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
consisting of all homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s from the space to itself with function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
as the group operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
. Homeomorphism groups are very important in the theory of topological spaces and in general are examples of automorphism groups. Homeomorphism groups are topological invariants in the sense that the homeomorphism groups of homeomorphic topological spaces are isomorphic as groups
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
.
Properties and Examples
There is a natural group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the homeomorphism group of a space on that space. If this action is transitive, then the space is said to be homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
.
Topology
As with other sets of maps between topological spaces, the homeomorphism group can be given a topology, such as the compact-open topologyCompact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
, making it into a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
.
In the category of topological spaces with homeomorphisms, object groups are exactly homeomorphism groups.
Mapping class group
In geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
especially, one considers the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
obtained by quotienting out by isotopy, called the mapping class group
Mapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
:

The MCG can also be interpreted as the 0th homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
,
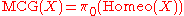 .
.This yields the short exact sequence:

In some applications, particularly surfaces, the homeomorphism group is studied via this short exact sequence, and by first studying the mapping class group and group of isotopically trivial homeomorphisms, and then (at times) the extension.

