
Hitchin system
Encyclopedia
In mathematics
, the Hitchin integrable system is an integrable system
introduced by Nigel Hitchin
in 1987. It lies on the crossroads
of the algebraic geometry
, theory of Lie algebra
s and integrable system theory. It also plays an important role in geometric Langlands correspondence over the field of complex number
s; related to conformal field theory
as certain limit of Knizhnik–Zamolodchikov equations. Almost all integrable systems of classical mechanics can be obtained as particular systems of the Hitchin system (or its certain generalization).
to the moduli space
of G-bundles for some reductive group
G, on some compact algebraic curve. This space is endowed with a canonical symplectic form. Suppose for simplicity that G=GL(n), the general linear group
; then the hamiltonians can be described as follows: the tangent space to G-bundles at the bundle F is

which by Serre duality
is dual to

so a pair
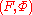
defines a point in the cotangent bundle. Taking
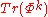 ,k=1,...,rank(G)
,k=1,...,rank(G)
one obtains elements in
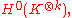
which is a vector space which does not depend on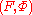 . So taking any basis in these vector spaces we obtain functions Hi, which are Hitchin's hamiltonians. The construction for general reductive group is similar and uses invariant polynomials on the Lie algebra
. So taking any basis in these vector spaces we obtain functions Hi, which are Hitchin's hamiltonians. The construction for general reductive group is similar and uses invariant polynomials on the Lie algebra
of G.
For trivial reasons these functions are algebraically independent, and some calculations show that their number is exactly half of the dimension of the phase space. The nontrivial part is a proof of Poisson commutativity of these functions. This is non-transparent from the algebraic geometry point of view, and one needs to go to differential geometric or Lie group viewpoints to obtain an explanation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hitchin integrable system is an integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
introduced by Nigel Hitchin
Nigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
in 1987. It lies on the crossroads
of the algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, theory of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and integrable system theory. It also plays an important role in geometric Langlands correspondence over the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s; related to conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
as certain limit of Knizhnik–Zamolodchikov equations. Almost all integrable systems of classical mechanics can be obtained as particular systems of the Hitchin system (or its certain generalization).
Description
Using the language of algebraic geometry, the phase space of the system is the cotangent bundleCotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
to the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of G-bundles for some reductive group
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
G, on some compact algebraic curve. This space is endowed with a canonical symplectic form. Suppose for simplicity that G=GL(n), the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
; then the hamiltonians can be described as follows: the tangent space to G-bundles at the bundle F is

which by Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
is dual to

so a pair
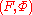
defines a point in the cotangent bundle. Taking
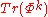 ,k=1,...,rank(G)
,k=1,...,rank(G)one obtains elements in
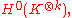
which is a vector space which does not depend on
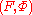 . So taking any basis in these vector spaces we obtain functions Hi, which are Hitchin's hamiltonians. The construction for general reductive group is similar and uses invariant polynomials on the Lie algebra
. So taking any basis in these vector spaces we obtain functions Hi, which are Hitchin's hamiltonians. The construction for general reductive group is similar and uses invariant polynomials on the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G.
For trivial reasons these functions are algebraically independent, and some calculations show that their number is exactly half of the dimension of the phase space. The nontrivial part is a proof of Poisson commutativity of these functions. This is non-transparent from the algebraic geometry point of view, and one needs to go to differential geometric or Lie group viewpoints to obtain an explanation.

