Heronian triangle
Encyclopedia
In geometry
, a Heronian triangle is a triangle
whose sidelengths and area
are all rational number
s. It is named after Hero of Alexandria
. Any such rational triangle can be scaled up to a corresponding triangle with integer sides and area, and often the term Heronian triangle is used to refer to the latter.
is Heronian, as the sidelengths of such a triangle are integer
s, and its area (being a right-angled triangle) is just half of the product of the two sides at the right angle.
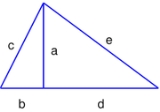
 An example of a Heronian triangle which is not right-angled is the one with sidelengths 5, 5, and 6, whose area is 12. This triangle is obtained by joining two copies of the right-angled triangle with sides 3, 4, and 5 by the side of length 4. This approach works in general, as illustrated in the picture to the right. One takes a Pythagorean triple (a, b, c), with c being largest, then another one (a, d, e), with e being largest, constructs the triangles with these sidelengths, and joins them together by the side of length a, to obtain a triangle with integer sidelengths c, e, and b + d, with rational area
An example of a Heronian triangle which is not right-angled is the one with sidelengths 5, 5, and 6, whose area is 12. This triangle is obtained by joining two copies of the right-angled triangle with sides 3, 4, and 5 by the side of length 4. This approach works in general, as illustrated in the picture to the right. One takes a Pythagorean triple (a, b, c), with c being largest, then another one (a, d, e), with e being largest, constructs the triangles with these sidelengths, and joins them together by the side of length a, to obtain a triangle with integer sidelengths c, e, and b + d, with rational area
 (one half times the base times the height).
(one half times the base times the height).
An interesting question to ask is whether all Heronian triangles can be obtained by joining together two right-angled triangles described in this procedure. The answer is no. If one takes the Heronian triangle with sidelengths 0.5, 0.5, and 0.6, which is just the triangle described above shrunk 10 times, it clearly cannot be decomposed into two triangles with integer sidelengths. Nor for example can a 5, 29, 30 triangle with area 72, since none of its altitude
s are integers. However, if one allows for Pythagorean triples with rational entries, not necessarily integers, then the answer is affirmative, because every altitude of a Heronian triangle is rational (since it equals twice the rational area divided by the rational base). Note that a triple with rational entries is just a scaled version of a triple with integer entries.
Proof of the theorem
Consider again the illustration to the right, where this time it is known that c, e, b + d, and the triangle area A are rational. We can assume that the notation was chosen so that the sidelength b + d is the largest, as then the perpendicular onto this side from the opposite vertex falls inside this segment. To show that the triples (a, b, c) and (a, d, e) are Pythagorean, one must prove that a, b, and d are rational.
Since the triangle area is
one can solve for a to find
which is rational, as both and
and  are rational. Left is to show that b and d are rational.
are rational. Left is to show that b and d are rational.
From the Pythagorean theorem
applied to the two right-angled triangles, one has
and
One can subtract these two, to find
or
or
The right-hand side is rational, because by assumption, c, e, and b + d are rational. Then, b − d is rational. This, together with b + d being rational implies by adding these up that b is rational, and then d must be rational too. Q.E.D.
as multiples of:





for integers m, n and k subject to the contraints:


 .
.
See also Heronian triangles with one angle equal to twice another.
by perimeter
, starts as in the following table.
Fundamental means that
the greatest common divisor
of the three side lengths equals 1.
. Since the area of an equilateral triangle with rational sides is an irrational number
, no equilateral triangle is Heronian. However, there is a unique sequence of Heronian triangles that are "almost equilateral" because the three sides, expressed as integers, are of the form n − 1, n, n + 1. The first few examples of these almost-equilateral triangles are set forth in the following table.
Subsequent values of n can be found by multiplying the last known value by 4, then subtracting the next to the last one (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, etc), as expressed in

where t denotes any row in the table.
This sequence can also be generated from the solutions to the Pell's equation
x² − 3y² = 1, which can in turn be derived from the regular continued fraction
expansion for √3.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Heronian triangle is a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
whose sidelengths and area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
are all rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. It is named after Hero of Alexandria
Hero of Alexandria
Hero of Alexandria was an ancient Greek mathematician and engineerEnc. Britannica 2007, "Heron of Alexandria" who was active in his native city of Alexandria, Roman Egypt...
. Any such rational triangle can be scaled up to a corresponding triangle with integer sides and area, and often the term Heronian triangle is used to refer to the latter.
Properties
Any triangle whose sidelengths are a Pythagorean triplePythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
is Heronian, as the sidelengths of such a triangle are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, and its area (being a right-angled triangle) is just half of the product of the two sides at the right angle.

 (one half times the base times the height).
(one half times the base times the height).An interesting question to ask is whether all Heronian triangles can be obtained by joining together two right-angled triangles described in this procedure. The answer is no. If one takes the Heronian triangle with sidelengths 0.5, 0.5, and 0.6, which is just the triangle described above shrunk 10 times, it clearly cannot be decomposed into two triangles with integer sidelengths. Nor for example can a 5, 29, 30 triangle with area 72, since none of its altitude
Altitude (triangle)
In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
s are integers. However, if one allows for Pythagorean triples with rational entries, not necessarily integers, then the answer is affirmative, because every altitude of a Heronian triangle is rational (since it equals twice the rational area divided by the rational base). Note that a triple with rational entries is just a scaled version of a triple with integer entries.
Theorem
Given a Heronian triangle, one can split it into two right-angled triangles, whose sidelengths form Pythagorean triples with rational entries.Proof of the theorem
Consider again the illustration to the right, where this time it is known that c, e, b + d, and the triangle area A are rational. We can assume that the notation was chosen so that the sidelength b + d is the largest, as then the perpendicular onto this side from the opposite vertex falls inside this segment. To show that the triples (a, b, c) and (a, d, e) are Pythagorean, one must prove that a, b, and d are rational.
Since the triangle area is

one can solve for a to find

which is rational, as both
 and
and  are rational. Left is to show that b and d are rational.
are rational. Left is to show that b and d are rational.From the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
applied to the two right-angled triangles, one has

and

One can subtract these two, to find

or

or

The right-hand side is rational, because by assumption, c, e, and b + d are rational. Then, b − d is rational. This, together with b + d being rational implies by adding these up that b is rational, and then d must be rational too. Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
Exact formula for Heronian triangles
All Heronian triangles can be generatedas multiples of:





for integers m, n and k subject to the contraints:


 .
.See also Heronian triangles with one angle equal to twice another.
Examples
The list of fundamental integer Heronian triangles, sorted by area and, if this is the same,by perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
, starts as in the following table.
Fundamental means that
the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of the three side lengths equals 1.
| Area | Perimeter | length b+d | length e | length c |
|---|---|---|---|---|
| 6 | 12 | 5 | 4 | 3 |
| 12 | 16 | 6 | 5 | 5 |
| 12 | 18 | 8 | 5 | 5 |
| 24 | 32 | 15 | 13 | 4 |
| 30 | 30 | 13 | 12 | 5 |
| 36 | 36 | 17 | 10 | 9 |
| 36 | 54 | 26 | 25 | 3 |
| 42 | 42 | 20 | 15 | 7 |
| 60 | 36 | 13 | 13 | 10 |
| 60 | 40 | 17 | 15 | 8 |
| 60 | 50 | 24 | 13 | 13 |
| 60 | 60 | 29 | 25 | 6 |
| 66 | 44 | 20 | 13 | 11 |
| 72 | 64 | 30 | 29 | 5 |
| 84 | 42 | 15 | 14 | 13 |
| 84 | 48 | 21 | 17 | 10 |
| 84 | 56 | 25 | 24 | 7 |
| 84 | 72 | 35 | 29 | 8 |
| 90 | 54 | 25 | 17 | 12 |
| 90 | 108 | 53 | 51 | 4 |
| 114 | 76 | 37 | 20 | 19 |
| 120 | 50 | 17 | 17 | 16 |
| 120 | 64 | 30 | 17 | 17 |
| 120 | 80 | 39 | 25 | 16 |
| 126 | 54 | 21 | 20 | 13 |
| 126 | 84 | 41 | 28 | 15 |
| 126 | 108 | 52 | 51 | 5 |
| 132 | 66 | 30 | 25 | 11 |
| 156 | 78 | 37 | 26 | 15 |
| 156 | 104 | 51 | 40 | 13 |
| 168 | 64 | 25 | 25 | 14 |
| 168 | 84 | 39 | 35 | 10 |
| 168 | 98 | 48 | 25 | 25 |
| 180 | 80 | 37 | 30 | 13 |
| 180 | 90 | 41 | 40 | 9 |
| 198 | 132 | 65 | 55 | 12 |
| 204 | 68 | 26 | 25 | 17 |
| 210 | 70 | 29 | 21 | 20 |
| 210 | 70 | 28 | 25 | 17 |
| 210 | 84 | 39 | 28 | 17 |
| 210 | 84 | 37 | 35 | 12 |
| 210 | 140 | 68 | 65 | 7 |
| 210 | 300 | 149 | 148 | 3 |
| 216 | 162 | 80 | 73 | 9 |
| 234 | 108 | 52 | 41 | 15 |
| 240 | 90 | 40 | 37 | 13 |
| 252 | 84 | 35 | 34 | 15 |
| 252 | 98 | 45 | 40 | 13 |
| 252 | 144 | 70 | 65 | 9 |
| 264 | 96 | 44 | 37 | 15 |
| 264 | 132 | 65 | 34 | 33 |
| 270 | 108 | 52 | 29 | 27 |
| 288 | 162 | 80 | 65 | 17 |
| 300 | 150 | 74 | 51 | 25 |
| 300 | 250 | 123 | 122 | 5 |
| 306 | 108 | 51 | 37 | 20 |
| 330 | 100 | 44 | 39 | 17 |
| 330 | 110 | 52 | 33 | 25 |
| 330 | 132 | 61 | 60 | 11 |
| 330 | 220 | 109 | 100 | 11 |
| 336 | 98 | 41 | 40 | 17 |
| 336 | 112 | 53 | 35 | 24 |
| 336 | 128 | 61 | 52 | 15 |
| 336 | 392 | 195 | 193 | 4 |
| 360 | 90 | 36 | 29 | 25 |
| 360 | 100 | 41 | 41 | 18 |
| 360 | 162 | 80 | 41 | 41 |
| 390 | 156 | 75 | 68 | 13 |
| 396 | 176 | 87 | 55 | 34 |
| 396 | 198 | 97 | 90 | 11 |
| 396 | 242 | 120 | 109 | 13 |
Almost-equilateral Heronian triangles
A Heronian triangle is a triangle with rational sides, area and inradiusIncircle and excircles of a triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
. Since the area of an equilateral triangle with rational sides is an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, no equilateral triangle is Heronian. However, there is a unique sequence of Heronian triangles that are "almost equilateral" because the three sides, expressed as integers, are of the form n − 1, n, n + 1. The first few examples of these almost-equilateral triangles are set forth in the following table.
| Side length | Area | Inradius | ||
|---|---|---|---|---|
| n − 1 | n | n + 1 | ||
| 3 | 4 | 5 | 6 | 1 |
| 13 | 14 | 15 | 84 | 4 |
| 51 | 52 | 53 | 1170 | 15 |
| 193 | 194 | 195 | 16296 | 56 |
| 723 | 724 | 725 | 226974 | 209 |
| 2701 | 2702 | 2703 | 3161340 | 780 |
| 10083 | 10084 | 10085 | 44031786 | 2911 |
| 37633 | 37634 | 37635 | 613283664 | 10864 |
Subsequent values of n can be found by multiplying the last known value by 4, then subtracting the next to the last one (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, etc), as expressed in

where t denotes any row in the table.
This sequence can also be generated from the solutions to the Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
x² − 3y² = 1, which can in turn be derived from the regular continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion for √3.
External links
- Online Encyclopedia of Integer Sequences Heronian
- Wm. Fitch Cheney, Jr., Heronian Triangles Am. Math. Montly 36 (1) (1929) 22-28.
- S. sh. Kozhegel'dinov On fundamental Heronian triangles Math. Notes 55 (2) (1994) 151-156.

