
Hermite's problem
Encyclopedia
Hermite's problem is an open problem in mathematics
posed by Charles Hermite
in 1848. He asked for a way of expressing real number
s as sequences of natural number
s, such that the sequence is eventually periodic precisely when the original number is a cubic irrational
.
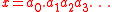
where a0 is an integer, the integer part of x, and a1, a2, a3… are integers between 0 and 9. Given this representation the number x is equal to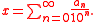
The real number x is a rational number
if and only if its decimal expansion is eventually periodic, that is if there are natural numbers N and p such that for every n ≥ N it is the case that an+p = an.
Another way of expressing numbers is to write them as continued fraction
s, as in: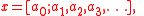
where a0 is an integer and a1, a2, a3… are natural numbers. From this representation we can recover x since
If x is a rational number then the sequence (an) terminates after finitely many terms. On the other hand, Euler proved that irrational numbers require an infinite sequence to express them as continued fractions. Moreover, this sequence is eventually periodic (again, so that there are natural numbers N and p such that for every n ≥ N we have an+p = an), if and only if x is a quadratic irrational
.
s that satisfy a polynomial of degree 1, while quadratic irrationals are algebraic numbers that satisfy a polynomial of degree 2. For both these sets of numbers we have a way to construct a sequence of natural numbers (an) with the property that each sequence gives a unique real number and such that this real number belongs to the corresponding set if and only if the sequence is eventually periodic.
In 1848 Charles Hermite wrote a letter to Carl Gustav Jacob Jacobi asking if this situation could be generalised, that is can one assign a sequence of natural numbers to each real number x such that the sequence is eventually periodic precisely when x is a cubic irrational, that is an algebraic number of degree 3? Or, more generally, for each natural number d is there a way of assigning a sequence of natural numbers to each real number x that can pick out when x is algebraic of degree d?
, but was unable to do so and whether this is the case remains unsolved.
Rather than generalising continued fractions, another approach to the problem is to generalise Minkowski's question mark function
. This function ? : [0, 1] → [0, 1] also picks out quadratic irrational numbers since ?(x) is rational if and only if x is either rational or a quadratic irrational number, and moreover x is rational if and only if ?(x) is a dyadic rational
, thus x is a quadratic irrational precisely when ?(x) is a non-dyadic rational number. Various generalisations of this function to either the unit square [0, 1] × [0, 1] or the two-dimensional simplex
have been made, though none has yet solved Hermite's problem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
posed by Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
in 1848. He asked for a way of expressing real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s as sequences of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, such that the sequence is eventually periodic precisely when the original number is a cubic irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
.
Motivation
A standard way of writing real numbers is by their decimal representation, such as: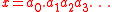
where a0 is an integer, the integer part of x, and a1, a2, a3… are integers between 0 and 9. Given this representation the number x is equal to
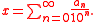
The real number x is a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
if and only if its decimal expansion is eventually periodic, that is if there are natural numbers N and p such that for every n ≥ N it is the case that an+p = an.
Another way of expressing numbers is to write them as continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s, as in:
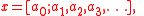
where a0 is an integer and a1, a2, a3… are natural numbers. From this representation we can recover x since

If x is a rational number then the sequence (an) terminates after finitely many terms. On the other hand, Euler proved that irrational numbers require an infinite sequence to express them as continued fractions. Moreover, this sequence is eventually periodic (again, so that there are natural numbers N and p such that for every n ≥ N we have an+p = an), if and only if x is a quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
.
Hermite's question
Rational numbers are algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s that satisfy a polynomial of degree 1, while quadratic irrationals are algebraic numbers that satisfy a polynomial of degree 2. For both these sets of numbers we have a way to construct a sequence of natural numbers (an) with the property that each sequence gives a unique real number and such that this real number belongs to the corresponding set if and only if the sequence is eventually periodic.
In 1848 Charles Hermite wrote a letter to Carl Gustav Jacob Jacobi asking if this situation could be generalised, that is can one assign a sequence of natural numbers to each real number x such that the sequence is eventually periodic precisely when x is a cubic irrational, that is an algebraic number of degree 3? Or, more generally, for each natural number d is there a way of assigning a sequence of natural numbers to each real number x that can pick out when x is algebraic of degree d?
Approaches
Sequences that attempt to solve Hermite's problem are often called multidimensional continued fractions. Jacobi himself came up with an early example, finding a sequence corresponding to each pair of real numbers (x,y) that acted as a higher dimensional analogue of continued fractions. He hoped to show that the sequence attached to (x, y) was eventually periodic if and only if both x and y belonged to a cubic number fieldCubic field
In mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three.-Definition:If K is a field extension of the rational numbers Q of degree [K:Q] = 3, then K is called a cubic field...
, but was unable to do so and whether this is the case remains unsolved.
Rather than generalising continued fractions, another approach to the problem is to generalise Minkowski's question mark function
Minkowski's question mark function
In mathematics, the Minkowski question mark function, sometimes called the slippery devil's staircase and denoted by ?, is a function possessing various unusual fractal properties, defined by Hermann Minkowski in 1904...
. This function ? : [0, 1] → [0, 1] also picks out quadratic irrational numbers since ?(x) is rational if and only if x is either rational or a quadratic irrational number, and moreover x is rational if and only if ?(x) is a dyadic rational
Dyadic rational
In mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...
, thus x is a quadratic irrational precisely when ?(x) is a non-dyadic rational number. Various generalisations of this function to either the unit square [0, 1] × [0, 1] or the two-dimensional simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
have been made, though none has yet solved Hermite's problem.

