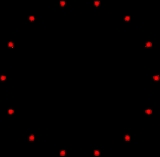
Heawood graph
Encyclopedia
In the mathematical
field of graph theory
, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood
.
, and all cycles in the graph have six or more edges. Every smaller cubic graph has shorter cycles, so this graph is the 6-cage
, the smallest cubic graph of girth
6. It is a distance-regular graph
.
There are 24 perfect matchings in the Heawood graph; for each matching, the set of edges not in the matching forms a Hamiltonian cycle. For instance, the figure shows the vertices of the graph placed on a cycle, with the internal diagonals of the cycle forming a matching. By subdividing the cycle edges into two matchings, we can partition the Heawood graph into three perfect matchings (that is, 3-color its edges
) in eight different ways (Brouwer). Every two perfect matchings, and every two Hamiltonian cycles, can be transformed into each other by a symmetry of the graph.
; that is, it can be embedded without crossings onto a torus
. One embedding of this type places its vertices and edges into three-dimensional Euclidean space
as the set of vertices and edges of a nonconvex polyhedron with the topology of a torus, the Szilassi polyhedron
.
The graph is named after Percy John Heawood
, who in 1890 proved that in every subdivision of the torus into polygons, the polygonal regions can be colored by at most seven colors. The Heawood graph forms a subdivision of the torus with seven mutually adjacent regions, showing that this bound is tight.
The Heawood graph is also the Levi graph
of the Fano plane
, the graph representing incidences between points and lines in that geometry. It has crossing number
3, and is the smallest cubic graph with that crossing number . Including the Heawood graph, there are 8 distinct graphs of order 14 with crossing number 3.
The Heawood graph is a unit distance graph
: it can be embedded in the plane such that adjacent vertices are exactly at distance one apart, with no two vertices embedded to the same point and no vertex embedded into a point within an edge. However, the known embeddings of this type lack any of the symmetries that are inherent in the graph.
PGL2(7), a group of order 336. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Heawood graph is a symmetric graph
. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Heawood graph, referenced as F014A, is the only cubic symmetric graph on 14 vertices.
The characteristic polynomial
of the Heawood graph is . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood
Percy John Heawood
Percy John Heawood was a British mathematician educated at Queen Elizabeth's School, Ipswich, and Exeter College, Oxford....
.
Combinatorial properties
The graph is cubicCubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
, and all cycles in the graph have six or more edges. Every smaller cubic graph has shorter cycles, so this graph is the 6-cage
Cage (graph theory)
In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.Formally, an -graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. It is known that an -graph exists...
, the smallest cubic graph of girth
Girth
In graph theory, the girth of a graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles , its girth is defined to be infinity....
6. It is a distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
.
There are 24 perfect matchings in the Heawood graph; for each matching, the set of edges not in the matching forms a Hamiltonian cycle. For instance, the figure shows the vertices of the graph placed on a cycle, with the internal diagonals of the cycle forming a matching. By subdividing the cycle edges into two matchings, we can partition the Heawood graph into three perfect matchings (that is, 3-color its edges
Edge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
) in eight different ways (Brouwer). Every two perfect matchings, and every two Hamiltonian cycles, can be transformed into each other by a symmetry of the graph.
Geometric and topological properties
The Heawood graph is a toroidal graphToroidal graph
In mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...
; that is, it can be embedded without crossings onto a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. One embedding of this type places its vertices and edges into three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
as the set of vertices and edges of a nonconvex polyhedron with the topology of a torus, the Szilassi polyhedron
Szilassi polyhedron
The Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces.Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem...
.
The graph is named after Percy John Heawood
Percy John Heawood
Percy John Heawood was a British mathematician educated at Queen Elizabeth's School, Ipswich, and Exeter College, Oxford....
, who in 1890 proved that in every subdivision of the torus into polygons, the polygonal regions can be colored by at most seven colors. The Heawood graph forms a subdivision of the torus with seven mutually adjacent regions, showing that this bound is tight.
The Heawood graph is also the Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
, the graph representing incidences between points and lines in that geometry. It has crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
3, and is the smallest cubic graph with that crossing number . Including the Heawood graph, there are 8 distinct graphs of order 14 with crossing number 3.
The Heawood graph is a unit distance graph
Unit distance graph
In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
: it can be embedded in the plane such that adjacent vertices are exactly at distance one apart, with no two vertices embedded to the same point and no vertex embedded into a point within an edge. However, the known embeddings of this type lack any of the symmetries that are inherent in the graph.
Algebraic properties
The automorphism group of the Heawood graph is isomorphic to the projective linear groupProjective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
PGL2(7), a group of order 336. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Heawood graph is a symmetric graph
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Heawood graph, referenced as F014A, is the only cubic symmetric graph on 14 vertices.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Heawood graph is
 . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.

