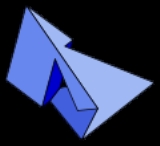
Szilassi polyhedron
Encyclopedia
 |
|
| Type | Toroidal polyhedron Toroidal polyhedron In geometry, a toroidal polyhedron is a polyhedron with a genus of 1 or greater, representing topological torus surfaces.Non-self-intersecting toroidal polyhedra are embedded tori, while self-intersecting toroidal polyhedra are toroidal as abstract polyhedra, which can be verified by their Euler... |
| Faces | 7 hexagons |
| Edges | 21 |
| Vertices | 14 |
| Euler characteristic Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
0 |
| Genus Genus (mathematics) In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It... |
1 |
| Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
6.6.6 |
| Symmetry group | ? |
| Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
Császár polyhedron Császár polyhedron In geometry, the Császár polyhedron is a nonconvex polyhedron, topologically a toroid, with 14 triangular faces.This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph K_7... |
| Properties | Nonconvex |
The Szilassi polyhedron is a nonconvex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, topologically a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, with seven hexagonal faces.
Each face of this polyhedron shares an edge with each other face. As a result, it requires seven colours to colour each adjacent face, providing the lower bound for the seven colour theorem. It has an axis of 180-degree symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
; three pairs of faces are congruent leaving one unpaired hexagon that has the same rotational symmetry as the polyhedron. The 14 vertices and 21 edges of the Szilassi polyhedron form an embedding of the Heawood graph
Heawood graph
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
onto the surface of a torus.
The tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
and the Szilassi polyhedron are the only two known polyhedra in which each face shares an edge with each other face. If a polyhedron with f faces is embedded onto a surface with h holes, in such a way that each face shares an edge with each other face, it follows by some manipulation of the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
that
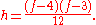
This equation is satisfied for the tetrahedron with h = 0 and f = 4, and for the Szilassi polyhedron with h = 1 and f = 7. The next possible solution, h = 6 and f = 12, would correspond to a polyhedron with 44 vertices and 66 edges, but it is not known whether such a polyhedron exists. More generally this equation can be satisfied only when f is congruent to 0, 3, 4, or 7 modulo 12.
The Szilassi polyhedron is named after Hungarian mathematician Lajos Szilassi, who discovered it in 1977. The dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
to the Szilassi polyhedron, the Császár polyhedron
Császár polyhedron
In geometry, the Császár polyhedron is a nonconvex polyhedron, topologically a toroid, with 14 triangular faces.This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph K_7...
, was discovered earlier by ; it has seven vertices, 21 edges connecting every pair of vertices, and 14 triangular faces. Like the Szilassi polyhedron, the Császár polyhedron has the topology of a torus.
External links
.- Szilassi Polyhedron - Papercraft model at CutOutFoldUp.com

